Exam 10: Comparisons Involving Means, Experimental Design and Analysis of Variance
Exam 1: Data and Statistics104 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Presentations65 Questions
Exam 3: Descriptive Statistics: Numerical Measures162 Questions
Exam 4: Introduction to Probability146 Questions
Exam 5: Discrete Probability Distributions121 Questions
Exam 6: Continuous Probability Distributions165 Questions
Exam 7: Sampling and Sampling Distributions131 Questions
Exam 8: Interval Estimation131 Questions
Exam 9: Hypothesis Tests136 Questions
Exam 10: Comparisons Involving Means, Experimental Design and Analysis of Variance208 Questions
Exam 11: Comparisons Involving Proportions and a Test of Independence94 Questions
Exam 12: Simple Linear Regression140 Questions
Exam 13: Multiple Regression146 Questions
Select questions type
When the p-value is used for hypothesis testing, the null hypothesis is rejected if
(Multiple Choice)
4.9/5  (34)
(34)
Which of the following is not a required assumption for the analysis of variance?
(Multiple Choice)
4.8/5  (39)
(39)
In a completely randomized experimental design, 11 experimental units were used for each of the 3 treatments. Part of the ANOVA table is shown below.
 a.Fill in the blanks in the above ANOVA table.
b.At 95% confidence, test to determine whether or not the means of the 3 populations are equal.
a.Fill in the blanks in the above ANOVA table.
b.At 95% confidence, test to determine whether or not the means of the 3 populations are equal.
(Essay)
4.9/5  (37)
(37)
Independent random samples taken at two companies provided the following information regarding annual salaries of the employees.
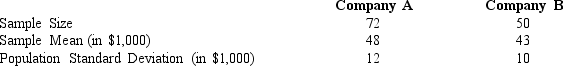 a.We want to determine whether or not there is a significant difference between the average salaries of the employees at the two companies. Compute the test statistic.
b.Compute the p-value; and at 95% confidence, test the hypotheses.
a.We want to determine whether or not there is a significant difference between the average salaries of the employees at the two companies. Compute the test statistic.
b.Compute the p-value; and at 95% confidence, test the hypotheses.
(Essay)
4.9/5  (40)
(40)
Exhibit 10-3
A statistics teacher wants to see if there is any difference in the abilities of students enrolled in statistics today and those enrolled five years ago. A sample of final examination scores from students enrolled today and from students enrolled five years ago was taken. You are given the following information.
 -Refer to Exhibit 10-3. The standard error of
-Refer to Exhibit 10-3. The standard error of 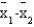 is
is
(Multiple Choice)
4.9/5  (43)
(43)
An ANOVA procedure is used for data that was obtained from four sample groups each comprised of five observations. The degrees of freedom for the critical value of F are
(Multiple Choice)
4.9/5  (36)
(36)
Exhibit 10-1
Salary information regarding male and female employees of a large company is shown below.
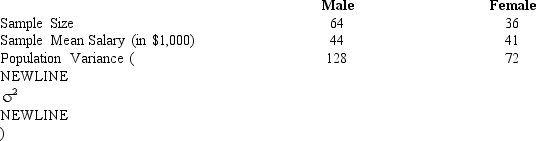 -Refer to Exhibit 10-1. The standard error for the difference between the two means is
-Refer to Exhibit 10-1. The standard error for the difference between the two means is
(Multiple Choice)
4.7/5  (34)
(34)
Exhibit 10-8
In order to determine whether or not there is a significant difference between the hourly wages of two companies, the following data have been accumulated. 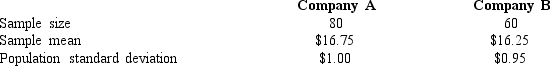 -Refer to Exhibit 10-8. A point estimate for the difference between the two sample means is
-Refer to Exhibit 10-8. A point estimate for the difference between the two sample means is
(Multiple Choice)
4.9/5  (43)
(43)
When the following hypotheses are being tested at a level of significance of H0: 1- 2 0
Ha: 1- 2 < 0
The null hypothesis will be rejected if the p-value is
(Multiple Choice)
4.8/5  (40)
(40)
Random samples were selected from three populations. The data obtained are shown below. Please note that the sample sizes are not equal.
 a.Compute the overall mean.
b.At 95% confidence, test to see if there is a significant difference among the means.
a.Compute the overall mean.
b.At 95% confidence, test to see if there is a significant difference among the means.
(Essay)
4.8/5  (36)
(36)
Exhibit 10-14
Part of an ANOVA table is shown below.
 -Refer to Exhibit 10-14. If at 95% confidence we want to determine whether or not the means of the populations are equal, the p-value is
-Refer to Exhibit 10-14. If at 95% confidence we want to determine whether or not the means of the populations are equal, the p-value is
(Multiple Choice)
4.7/5  (39)
(39)
Three universities in your state decided to administer the same comprehensive examination to the recipients of MBA degrees from the three institutions. From each institution, MBA recipients were randomly selected and were given the test. The following table shows the scores of the students from each university.
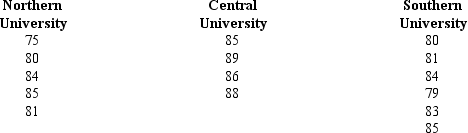 At = 0.01, test to see if there is any significant difference in the average scores of the students from the three universities. (Note that the sample sizes are not equal.) Use both the critical and p-value approaches.
At = 0.01, test to see if there is any significant difference in the average scores of the students from the three universities. (Note that the sample sizes are not equal.) Use both the critical and p-value approaches.
(Essay)
4.9/5  (34)
(34)
For a one-tailed test (lower tail) at 93.7% confidence, Z =
(Multiple Choice)
4.9/5  (32)
(32)
Exhibit 10-1
Salary information regarding male and female employees of a large company is shown below.
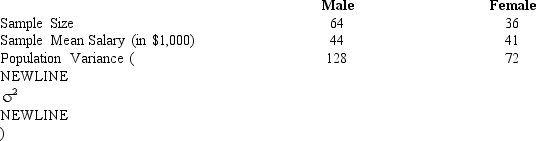 -Refer to Exhibit 10-1. If you are interested in testing whether or not the average salary of males is significantly greater than that of females, the test statistic is
-Refer to Exhibit 10-1. If you are interested in testing whether or not the average salary of males is significantly greater than that of females, the test statistic is
(Multiple Choice)
4.8/5  (29)
(29)
When each data value in one sample is matched with a corresponding data value in another sample, the samples are known as
(Multiple Choice)
4.7/5  (34)
(34)
A credit company has gathered information regarding the average amount owed by people under 30 years old and by people over 30 years. Independent random samples were taken from both age groups. You are given the following information.
 Construct a 95% confidence interval for the difference between the average amounts owed by the two age groups.
Construct a 95% confidence interval for the difference between the average amounts owed by the two age groups.
(Short Answer)
4.8/5  (35)
(35)
Exhibit 10-14
Part of an ANOVA table is shown below.
 -Refer to Exhibit 10-14. The number of degrees of freedom corresponding to within treatments is
-Refer to Exhibit 10-14. The number of degrees of freedom corresponding to within treatments is
(Multiple Choice)
4.8/5  (41)
(41)
In order to test to see if there is any significant difference in the mean number of units produced per week by each of three production methods, the following data were collected. (Please note that the sample sizes are not equal.)
 a.Compute.
b.At the = 0.05 level of significance, is there any difference in the mean number of units produced per week by each method? Show the complete ANOVA table. Use both the critical and p-value approaches.
a.Compute.
b.At the = 0.05 level of significance, is there any difference in the mean number of units produced per week by each method? Show the complete ANOVA table. Use both the critical and p-value approaches.
(Essay)
4.8/5  (27)
(27)
Independent random samples taken at two local malls provided the following information regarding purchases by patrons of the two malls.
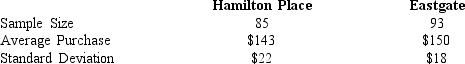 We want to determine whether or not there is a significant difference between the average purchases by the patrons of the two malls.
a.Give the hypotheses for the above.
b.Compute the test statistic.
c.At 95% confidence, test the hypotheses.
We want to determine whether or not there is a significant difference between the average purchases by the patrons of the two malls.
a.Give the hypotheses for the above.
b.Compute the test statistic.
c.At 95% confidence, test the hypotheses.
(Essay)
4.8/5  (29)
(29)
Showing 161 - 180 of 208
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)