Exam 4: Inequalities and Linear Programming
Exam 1: Linear Equations and Functions245 Questions
Exam 2: Quadratic and Other Special Functions120 Questions
Exam 3: Matrices230 Questions
Exam 4: Inequalities and Linear Programming119 Questions
Exam 5: Exponential and Logarithmic Functions109 Questions
Exam 6: Mathematics of Finance131 Questions
Exam 7: Introduction to Probability180 Questions
Exam 8: Further Topics in Probability and Data Description114 Questions
Exam 9: Derivatives249 Questions
Exam 10: Derivatives172 Questions
Exam 11: Derivatives Continued139 Questions
Exam 12: Indefinite Integrals120 Questions
Exam 13: Definite Integrals - Techniques370 Questions
Exam 13: A: Definite Integrals - Techniques370 Questions
Exam 14: Functions of Two or More Variables122 Questions
Exam 15: Algebraic Concepts 240 Questions
Exam 15: Algebraic Concepts 374 Questions
Exam 15: Algebraic Concepts 496 Questions
Exam 15: Algebraic Concepts 599 Questions
Select questions type
Use the simplex method to find the optimal solution.
Maximize 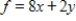 subject to
subject to 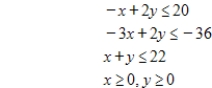
(Multiple Choice)
4.8/5  (37)
(37)
Solve the following minimization problem by solving the primal problem with the simplex method.
Minimize 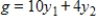 subject to
subject to
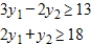
(Multiple Choice)
4.8/5  (31)
(31)
The Wellbuilt Company produces two types of wood chippers, economy and deluxe. The deluxe model requires 4 hours to assemble and 0.5 hour to paint, and the economy model requires 2 hours to assemble and 1 hour to paint. The maximum number of assembly hours available is 22 per day, and the maximum number of painting hours available is 8 per day. Let x represent the number of deluxe models and y represent the number of economy models. Write the system of inequalities that describes the constraints on the number of each type of wood chipper produced.
(Multiple Choice)
4.8/5  (35)
(35)
In a laboratory experiment, two separate foods are given to experimental animals. Each food contains essential ingredients, A and B, for which the animals have a minimum requirement, and each food also has an ingredient C, which can be harmful to the animals. The table below summarizes this information.
 How many grams of foods 1 and 2 will satisfy the requirements for A and B and minimize the amount of ingredient C that is ingested? Also what is the minimum amount of ingredient C ingested?
How many grams of foods 1 and 2 will satisfy the requirements for A and B and minimize the amount of ingredient C that is ingested? Also what is the minimum amount of ingredient C ingested?
(Multiple Choice)
4.9/5  (37)
(37)
The Wellbuilt Company produces two types of wood chippers, economy and deluxe. The deluxe model requires 3 hours to assemble and 4 hour to paint, and the economy model requires 2 hours to assemble and 1 hour to paint. The maximum number of assembly hours available is 24 per day, and the maximum number of painting hours available is 17 per day. Let x represent the number of deluxe models and y represent the number of economy models. Graph the solution of the system of inequalities and find the corners of the solution region.
(Multiple Choice)
5.0/5  (40)
(40)
Apex Motors manufactures luxury cars and sport utility vehicles. The most likely customers are high-income men and women, and company managers want to initiate an advertising campaign targeting these groups. They plan to run 1-minute spots on business/investment programs, where they can reach 7 million women and 4 million men from their target groups. They also plan 1-minute spots during sporting events, where they can reach 2 million women and 12 million men from their target groups. Apex feels that the ads must reach at least 32 million women and at least 20 million men who are prospective customers. Let x represent the number of minutes of business/investment program commercials and y represent the number of minutes of sporting events commercials. Graph the region determined by the constraint inequalities.
(Multiple Choice)
4.9/5  (38)
(38)
A simplex matrix for a standard maximization problem is given. Indicate whether or not the solution shown is complete (optimal). If the solution is not complete, find the next pivot or indicate that no solution exists. 
(Multiple Choice)
4.9/5  (44)
(44)
Nekita Corporation assembles cell phones and camera cell phones at two different factories within the same city. During each hour at the first factory, 15 cell phones and 30 camera cell phones can be assembled at a cost of $130/hour. During each hour at the second factory, 10 cell phones and 60 camera cell phones can be assembled at a cost of $160/hour. If Nekita expects weekly orders for at least 15,000 cell phones and at least 45,000 camera cell phones, how many hours per week should it schedule at each location to be able to fill the orders at minimum cost? What is the minimum cost?
(Multiple Choice)
4.8/5  (30)
(30)
A company manufactures commercial heating system components and domestic furnaces at its factories in Monaca, PA and Hamburg, NY. At the Monaca plant, no more than 1000 units per day can be produced, and the number of commercial components cannot exceed 100 more than half the number of domestic furnaces. At the Hamburg plant, no more than 850 units per day can be produced. The profit on each commercial component is $400 at the Monaca plant and $390 at the Hamburg plant. The profit on each domestic furnace is $200 at the Monaca plant and $215 at the Hamburg plant. If there is a rush order for 500 commercial components and 750 domestic furnaces, how many of each should be produced at each plant in order to maximize profits? Find the maximum profit. Note: Assume that exactly enough units are produced to fill the rush order.
(Multiple Choice)
4.9/5  (34)
(34)
Form the simplex matrix, and identify the first pivot entry. Minimize 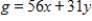 subject to
subject to 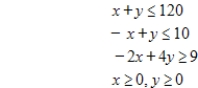
(Multiple Choice)
4.8/5  (25)
(25)
Tire Corral has $6,000 available per month for advertising. Newspaper ads cost $100 each and can occur a maximum of 21 times per month. Radio ads cost $300 each and can occur a maximum of 28 times per month at this price. Each newspaper ad reaches 6,750 men over 20 years of age, and each radio ad reaches 8,500 of these men. The company wants to maximize the number of ad exposures to this group. How many of each ad should it purchase? What is the maximum possible number of exposures? Round your answers to the nearest whole number if necessary.
(Multiple Choice)
4.8/5  (25)
(25)
A chemical storage tank has a capacity of 200 tons. Currently, the tank contains 50 tons of a mixture that has 10% of a certain active chemical and 1.8% of other inert ingredients. The owners of the tank want to replenish the supply in the tank and will purchase some combination of two available mixes. Mix 1 contains 70% of the active chemical and 3% of the inert ingredients; its cost is $106 per ton. Mix 2 contains 30% of the active chemical and 1% of the inert ingredients; its cost is $42 per ton. The desired final mixture should have at least 40% of the active chemical and at most 2% of the inert ingredients. How many tons of each mix should be purchased to obtain the desired final mixture at minimum cost? Find the minimum cost. Note that at least 40% of the active chemical means; 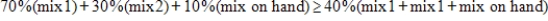 .
.
(Multiple Choice)
5.0/5  (36)
(36)
A medical clinic performs three types of medical tests that use the same machines. Tests A, B, and C take 15 minutes, 30 minutes, and 1 hour, respectively, with respective profits of $90, $120 and $150. The clinic has 4 machines available. One person is qualified to do test A, two to do test B, and one to do test C. If the clinic has a rush of customers for these tests, how many of each type should it schedule in a 9 - hour day to maximize its profit? Round your profit to the nearest dollar and another answers - to the nearest whole number.
(Multiple Choice)
4.7/5  (40)
(40)
Suppose that an experiment that involves learning in animals requires placing white mice and rabbits into separate, controlled environments, environment I and environment II. The maximum amount of time available in environment I is 300 minutes, and the maximum amount of time available in environment II is 400 minutes. The white mice must spend 20 minutes in environment I and 35 minutes in environment II, and the rabbits must spend 45 minutes in environment I and 50 minutes in environment II. Let x represent number of white mice and y represent number of rabbits. Determine the system of inequalities that describes the constraints on the number of each type of animal used in the experiment. Then graph the solution of the system of inequalities.
(Multiple Choice)
4.8/5  (35)
(35)
A primal maximization problem is given. Solve both the primal and dual problems with the simplex method.
Maximize 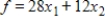 subject to
subject to
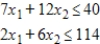
(Multiple Choice)
4.8/5  (29)
(29)
At one of its factories, a jeans manufacturer makes two styles: #891 and #917. Each pair of style-891 takes 10 minutes to cut out and 20 minutes to assemble and finish. Each pair of style-917 takes 10 minutes to cut out and 30 minutes to assemble and finish. The plant has enough workers to provide at most 7,500 minutes per day for cutting and at most 19,500 minutes per day for assembly and finishing. The profit on each pair of style-891 is $6.00 and the profit on each pair of style-917 is $8.50. How many pairs of each style should be produced per day to obtain maximum profit? Find the maximum daily profit. Round your profit to the nearest cent and anothet answers - to the nearest whole number.
(Multiple Choice)
4.8/5  (36)
(36)
Write the dual maximization problem. Be sure to rename the variables.
Minimize 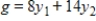 subject to
subject to
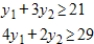
(Multiple Choice)
4.8/5  (30)
(30)
Three factories each dump waste water containing three different types of pollutants into a river. State regulations require the factories to treat their waste in order to reduce pollution levels. The table shows the possible percent reduction of each pollutant at each site and the cost per ton to process the waste.
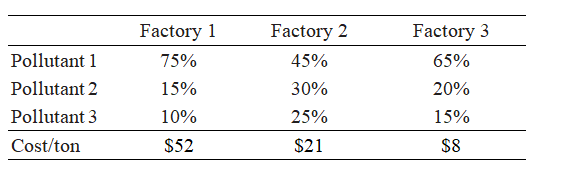
If the state requires a reduction of at least 65 tons per day of pollutant 1, at least 40 tons per day of pollutant 2, and at least 20 tons per day of pollutant 3, find the number of tons of waste that must be treated each day at each site so that the state's requirements are satisfied and the treatment costs are minimized. Find the minimum cost.
If the state requires a reduction of at least 65 tons per day of pollutant 1, at least 40 tons per day of pollutant 2, and at least 20 tons per day of pollutant 3, find the number of tons of waste that must be treated each day at each site so that the state's requirements are satisfied and the treatment costs are minimized. Find the minimum cost.
(Multiple Choice)
4.9/5  (32)
(32)
Showing 101 - 119 of 119
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)