Exam 4: Inequalities and Linear Programming
Exam 1: Linear Equations and Functions245 Questions
Exam 2: Quadratic and Other Special Functions120 Questions
Exam 3: Matrices230 Questions
Exam 4: Inequalities and Linear Programming119 Questions
Exam 5: Exponential and Logarithmic Functions109 Questions
Exam 6: Mathematics of Finance131 Questions
Exam 7: Introduction to Probability180 Questions
Exam 8: Further Topics in Probability and Data Description114 Questions
Exam 9: Derivatives249 Questions
Exam 10: Derivatives172 Questions
Exam 11: Derivatives Continued139 Questions
Exam 12: Indefinite Integrals120 Questions
Exam 13: Definite Integrals - Techniques370 Questions
Exam 13: A: Definite Integrals - Techniques370 Questions
Exam 14: Functions of Two or More Variables122 Questions
Exam 15: Algebraic Concepts 240 Questions
Exam 15: Algebraic Concepts 374 Questions
Exam 15: Algebraic Concepts 496 Questions
Exam 15: Algebraic Concepts 599 Questions
Select questions type
A farm co-op has over 6,000 acres available to plant with corn and soybeans. The farm co-op's maximum profit for planting 6,000 acres is $315,000 and the maximum profit for 6,008 acres is $315,320. What is the profit value of each additional acre of land? This value is called the shadow price of an acre of land. Round your answer to the nearest cent if necessary.
(Multiple Choice)
4.9/5  (34)
(34)
Solve the following linear programming problem.
Maximize 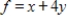 subject to
subject to
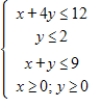
(Multiple Choice)
4.9/5  (41)
(41)
Solve the following linear programming problem.
Minimize 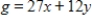 subject to
subject to
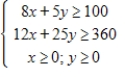
(Multiple Choice)
4.9/5  (29)
(29)
CDF Appliances has assembly plants in Atlanta and Fort Worth where they produce a variety of kitchen appliances, including a 12-cup coffee maker and a cappuccino machine. In each hour at the Atlanta plant, 160 of the 12-cup models and 200 of the cappuccino machines can be assembled and the hourly cost is $780. In each hour at the Fort Worth plant, 800 of the 12-cup models and 200 of the cappuccino machines can be assembled and the hourly cost is $2,120. CDF Appliances expects orders each week for at least 64,000 of the 12-cup models and at least 40,000 of the cappuccino machines. How many hours per week should each plant be operated in order to provide inventory for the orders at minimum cost? Find the minimum cost.
(Multiple Choice)
4.8/5  (38)
(38)
A simplex matrix is given. In this case the solution is complete, so identify the maximum value of f and a set of values of the variables that gives this maximum value. If multiple solutions may exist, indicate this and locate the next pivot. 
(Multiple Choice)
4.8/5  (29)
(29)
Use the simplex method to maximize the function (if possible) subject to the given constraints. If there is no solution, indicate this; if multiple solutions exist, give one solution.
Maximize 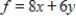 subject to
subject to
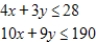
(Multiple Choice)
4.7/5  (38)
(38)
Form the matrix associated with the given minimization problem and find its transpose.
Minimize 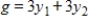 subject to
subject to
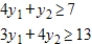
(Multiple Choice)
4.8/5  (34)
(34)
The graph of the boundary equations for the system of inequalities is shown with that system. Locate the solution region and find the corners. 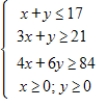
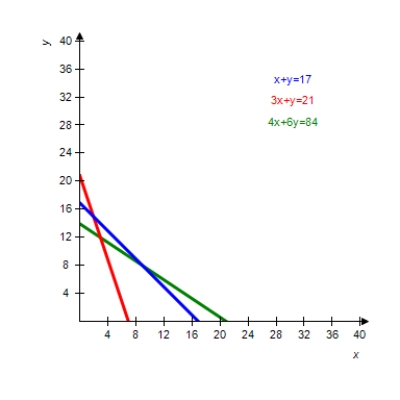
(Multiple Choice)
4.8/5  (36)
(36)
Use Excel or another technology to solve the following optimization problem.
Minimize 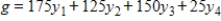 subject to
subject to
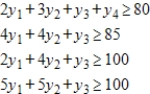
(Multiple Choice)
4.9/5  (37)
(37)
Solve the following linear programming problem.
Minimize 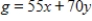 subject to
subject to
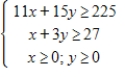
(Multiple Choice)
4.8/5  (33)
(33)
The graph of the boundary equations for the system of inequalities is shown with that system. Locate the solution region and find the corners. 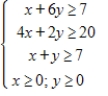
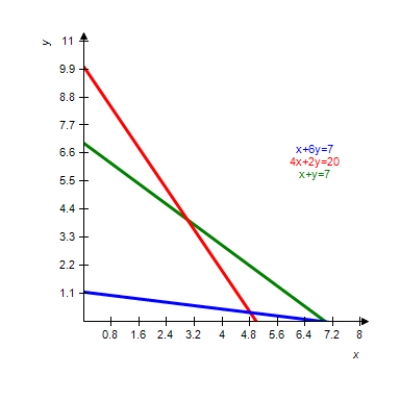
(Multiple Choice)
4.9/5  (25)
(25)
State the given problem in a form from which the simplex matrix can be formed (that is, as a maximization problem with 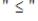 constraints).
Minimize
constraints).
Minimize 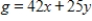 subject to
subject to 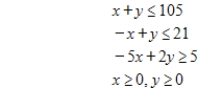
(Multiple Choice)
4.8/5  (32)
(32)
A cereal manufacturer makes two different kinds of cereal, Senior Citizen's Feast and Kids Go. Each pound of Senior Citizen's Feast requires 0.6 lb of wheat and 0.2 lb of vitamin-enriched syrup, and each pound of Kids Go requires 0.4 lb of wheat, 0.2 lb of sugar, and 0.2 lb of vitamin-enriched syrup. Suppliers can deliver at most 2,800 lb of wheat, at most 800 lb of sugar, and at least 1,000 lb of the vitamin-enriched syrup. If the profit is $0.80 on each pound of Senior Citizen's Feast and $1.00 on each pound of Kids Go, find the number of pounds of each cereal that should be produced to obtain maximum profit. Find the maximum profit. Round your profit to the nearest cent, another answers - to the nearest whole number.
(Multiple Choice)
4.8/5  (39)
(39)
Set up the simplex matrix used to solve the linear programming problem. Assume all variables are nonnegative.
Maximize 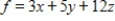 subject to
subject to
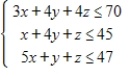
(Multiple Choice)
4.9/5  (34)
(34)
Use the simplex method to maximize the given function. Assume all variables are nonnegative.
Maximize 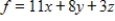 subject to
subject to
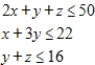
(Multiple Choice)
4.8/5  (35)
(35)
The final simple matrix for a minimization problem is given below. Find the solution. 
(Multiple Choice)
4.8/5  (31)
(31)
The Janie Gioffre Drapery Company makes three types of draperies at two different locations. At location I, it can make 10 pairs of deluxe drapes, 20 pairs of better drapes, and 13 pairs of standard drapes per day. At location II, it can make 20 pairs of deluxe drapes, 50 pairs of better drapes, and 6 pairs of standard drapes per day. The company has orders for 2,000 pairs of deluxe drapes, 4,200 pairs of better drapes, and 1,200 pairs of standard drapes. If the daily costs are $700 per day at location I and $800 per day at location II, how many days should Janie schedule at each location in order to fill the orders at minimum cost? Find the minimum cost. Round your answers to the nearest whole number if necessary.
(Multiple Choice)
4.8/5  (33)
(33)
A farm co-op has over 40,500 gallons of fertilizer/herbicide available to use when planting corn and soybeans. The farm co-op's maximum profit for using 40,500 gallons of fertilizer/herbicide is $315,009 and the maximum profit for 40,508 gallons is $315,034. What is the profit value of each additional gallon of fertilizer/herbicide (that is, the shadow price of a gallon of fertilizer/herbicide)? Round your answer to the nearest cent if necessary.
(Multiple Choice)
4.8/5  (35)
(35)
Showing 41 - 60 of 119
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)