Exam 4: Inequalities and Linear Programming
Exam 1: Linear Equations and Functions245 Questions
Exam 2: Quadratic and Other Special Functions120 Questions
Exam 3: Matrices230 Questions
Exam 4: Inequalities and Linear Programming119 Questions
Exam 5: Exponential and Logarithmic Functions109 Questions
Exam 6: Mathematics of Finance131 Questions
Exam 7: Introduction to Probability180 Questions
Exam 8: Further Topics in Probability and Data Description114 Questions
Exam 9: Derivatives249 Questions
Exam 10: Derivatives172 Questions
Exam 11: Derivatives Continued139 Questions
Exam 12: Indefinite Integrals120 Questions
Exam 13: Definite Integrals - Techniques370 Questions
Exam 13: A: Definite Integrals - Techniques370 Questions
Exam 14: Functions of Two or More Variables122 Questions
Exam 15: Algebraic Concepts 240 Questions
Exam 15: Algebraic Concepts 374 Questions
Exam 15: Algebraic Concepts 496 Questions
Exam 15: Algebraic Concepts 599 Questions
Select questions type
Use the simplex method, Excel, or another technology to find the solution of the problem given below. Assume all variables are nonnegative. 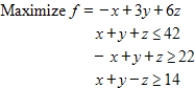
(Multiple Choice)
4.7/5  (36)
(36)
Suppose a primal minimization problem and its dual maximization problem were solved by using the simplex method on the dual problem. The final simplex matrix is given. Find the solution of the minimization problem. Use y1, y2, y3 as the variables and g as the function. 
(Multiple Choice)
4.7/5  (38)
(38)
The James MacGregor Mining Company owns three mines: I, II, and III. Three grades of ore, A, B, and C, are mined at these mines. For each grade of ore, the number of tons per week available from each mine and the number of tons per week required to fill orders are given in the following table.
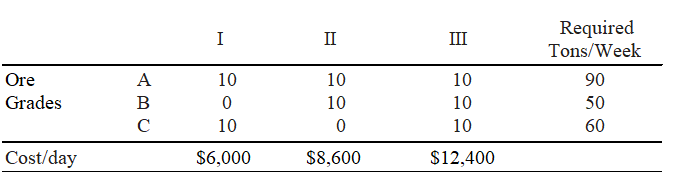
Find the number of days that the company should operate each mine so that orders are filled at minimum cost. Find the minimum cost.
Find the number of days that the company should operate each mine so that orders are filled at minimum cost. Find the minimum cost.
(Multiple Choice)
4.8/5  (28)
(28)
A simplex matrix for a standard maximization problem is given. Indicate whether or not the solution shown is complete (optimal). If the solution is not complete, find the next pivot or indicate that no solution exists. 
(Multiple Choice)
4.9/5  (43)
(43)
Find the transpose of the matrix associated with the given minimization problem. y
Minimize 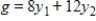 subject to
subject to
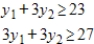
(Multiple Choice)
4.8/5  (34)
(34)
An ice cream company is planning its production for next week. Demand for premium and light ice creams continues to outpace the company's production capacities. Two resources used in ice cream production are in short supply for next week. The mixing machine will be available for only 150 hours, and only 30000 gallons of high grade milk will be available. One hundred gallons of premium ice-cream requires 0.6 hour of mixing and 180 gallons of milk. One hundred gallons of light ice cream requires 1 hour of mixing and 140 gallons of milk. If company earns a profit of $100 per hundred gallons on both of its ice creams, how many gallons of premium and of light ice cream should company produce next week to maximize profit? How much profit will result? Round your profit to the nearest cent and another answers - to the nearest whole number.
(Multiple Choice)
4.8/5  (37)
(37)
Use the simplex method, Excel, or another technology, to find the solution of the problem given below. Assume all variables are nonnegative. 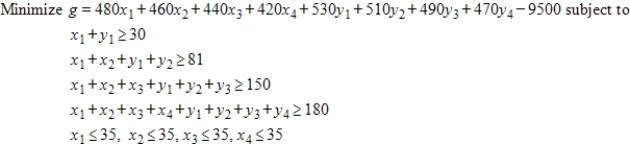
(Multiple Choice)
4.9/5  (42)
(42)
Use the simplex method to find the optimal solution.
Minimize 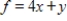 subject to
subject to 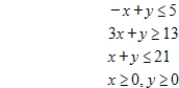
(Multiple Choice)
4.9/5  (24)
(24)
A farm co-op has 6,008 acres available to plant with corn and soybeans. Each acre of corn requires 9 gallons of fertilizer/herbicide and 0.75 hour of labor to harvest. Each acre of soybeans requires 3 gallons of fertilizer/herbicide and 1hour of labor to harvest. The co-op has available at most 40,500 gallons of fertilizer/herbicide and at most 5,250 hours of labor for harvesting. Find the maximum profit if the profits per acre are $70 for corn and $55 for soybeans. Round your answer to the nearest cent if necessary.
(Multiple Choice)
4.9/5  (32)
(32)
Use the simplex method, Excel, or another technology to solve. 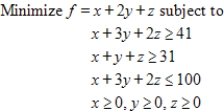
(Multiple Choice)
4.9/5  (35)
(35)
Convert the constraint inequalities 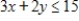 and
and 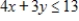 to equations containing slack variables.
to equations containing slack variables.
(Multiple Choice)
5.0/5  (40)
(40)
Use the simplex method to maximize the function (if possible) subject to the given constraints. If there is no solution, indicate this; if multiple solutions exist, give one solution.
Maximize 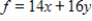 subject to
subject to
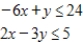
(Multiple Choice)
4.8/5  (37)
(37)
The Video Star Company makes two different models of DVD players, which are assembled on two different assembly lines. Line 1 can assemble 32 units of the Star model and 44 units of the Prostar model per hour, and Line 2 can assemble 150 units of the Star model and 40 units of the Prostar model per hour. The company needs to produce at least 260 units of the Star model and 225 units of the Prostar model to fill an order. Let x represent the number of assembly hours for Line 1 and y represent the number of assembly hours for Line 2. Write the inequalities that describe the production constraints on the number of each type of DVD player needed to fill the order.
(Multiple Choice)
4.9/5  (25)
(25)
Solve the following linear programming problem.
Maximize 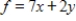 subject to
subject to
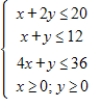
(Multiple Choice)
4.9/5  (42)
(42)
Use the given feasible region determined by the constraint inequalities to find the maximum and minimum of the given objective function (if they exist). 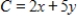
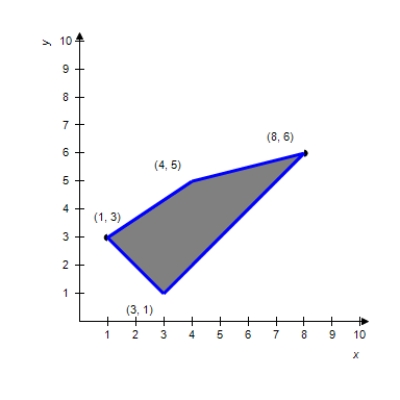
(Multiple Choice)
4.9/5  (45)
(45)
Write the dual maximization problem. Be sure to rename the variables.
Minimize 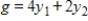 subject to
subject to
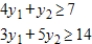
(Multiple Choice)
4.8/5  (37)
(37)
A company manufactures two types of electric hedge trimmers, one of which is cordless. The cord-type trimmer requires 2 hours to make, and the cordless model requires 7 hours. The company has only 800 work hours to use in manufacturing each day, and the packaging department can package only 300 trimmers per day. Let x represent the number of cord type models and y represent the number of cordless models. Write the inequalities that describe the constraints on the number of each type of hedge trimmer produced.
(Multiple Choice)
4.7/5  (34)
(34)
Showing 81 - 100 of 119
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)