Exam 16: Superposition and Standing Waves
Exam 1: Systems of Measurement86 Questions
Exam 2: Motion in One Dimension103 Questions
Exam 3: Motion in Two and Three Dimensions67 Questions
Exam 4: Newtons Laws117 Questions
Exam 5: Applications of Newtons Laws75 Questions
Exam 6: Work and Energy71 Questions
Exam 7: Conservation of Energy73 Questions
Exam 8: Systems of Particles and Conservation of Linear Momentum107 Questions
Exam 9: Rotation119 Questions
Exam 10: Conservation of Angular Momentum67 Questions
Exam 11: Gravity90 Questions
Exam 12: Static Equilibrium and Elasticity65 Questions
Exam 13: Fluids91 Questions
Exam 14: Oscillations138 Questions
Exam 15: Wave Motion122 Questions
Exam 16: Superposition and Standing Waves125 Questions
Exam 17: Temperature and the Kinetic Theory of Gases85 Questions
Exam 18: Heat and the First Law of Thermodynamics114 Questions
Exam 19: The Second Law of Thermodynamics61 Questions
Exam 20: Thermal Properties and Processes54 Questions
Select questions type
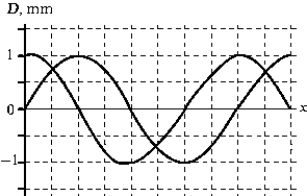 The figure shows two waves traveling in the positive-x direction. The phase difference between these two waves is
The figure shows two waves traveling in the positive-x direction. The phase difference between these two waves is
(Multiple Choice)
4.8/5  (39)
(39)
The reason we can tell the difference between a trumpet and a clarinet when they both play the same pitch is that they have
(Multiple Choice)
5.0/5  (38)
(38)
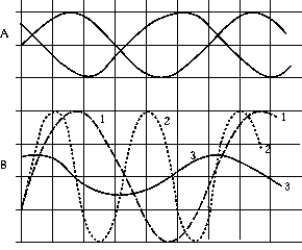 In graph A, two waves are shown at a given instant. What is the number of the curve in graph B that represents the wave resulting from the superposition of the two waves in A at this instant?
In graph A, two waves are shown at a given instant. What is the number of the curve in graph B that represents the wave resulting from the superposition of the two waves in A at this instant?
(Multiple Choice)
4.7/5  (29)
(29)
The standing waves in air in a pipe of length L that is open at one end and closed at the other have a speed v. The frequencies of the three lowest harmonics are
(Multiple Choice)
4.9/5  (43)
(43)
 A stretched string is fixed at points 1 and 5. When it is vibrating at the second harmonic frequency, the nodes of the standing wave are at points
A stretched string is fixed at points 1 and 5. When it is vibrating at the second harmonic frequency, the nodes of the standing wave are at points
(Multiple Choice)
4.8/5  (41)
(41)
 An examination of this frequency spectrum allows you to conclude that
An examination of this frequency spectrum allows you to conclude that
(Multiple Choice)
4.9/5  (43)
(43)
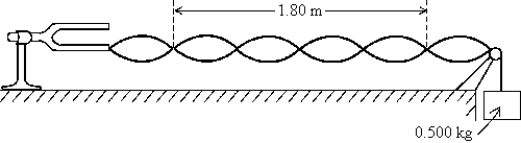 A string is connected to a tuning fork whose frequency is 80.0 Hz and is held under tension by 0.500 kg. The tuning fork causes the string to vibrate as shown. The mass per unit length for the string is
A string is connected to a tuning fork whose frequency is 80.0 Hz and is held under tension by 0.500 kg. The tuning fork causes the string to vibrate as shown. The mass per unit length for the string is
(Multiple Choice)
4.8/5  (37)
(37)
If both the tension and the length of a vibrating string are doubled while the linear density remains constant, the fundamental frequency of the string is multiplied by
(Multiple Choice)
4.8/5  (35)
(35)
A standing wave is created by oscillating a taut string at a frequency that corresponds to one of the resonant frequencies. The amplitude of the antinodes is very much larger than the amplitude of the oscillator. Does this violate the conservation of energy principle? Explain why. 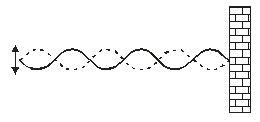
(Multiple Choice)
4.9/5  (39)
(39)
A string with mass density equal to 0.0025 kg/m is fixed at both ends and at a tension of 290 N. Resonant frequencies are found at 558 Hz and the next one at 744 Hz. What is the fundamental frequency of the string?
(Multiple Choice)
4.8/5  (38)
(38)
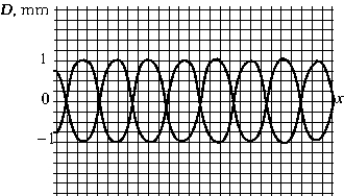 The figure shows two waves traveling in the positive-x direction. The amplitude of the resultant wave is
The figure shows two waves traveling in the positive-x direction. The amplitude of the resultant wave is
(Multiple Choice)
4.7/5  (30)
(30)
 The sound wave in an organ tube has a wavelength that is equal to the distance between
The sound wave in an organ tube has a wavelength that is equal to the distance between
(Multiple Choice)
4.9/5  (40)
(40)
Use the figure to the right to answer the next problems.
The graph shows three harmonics.  -The frequency spectrum of the composite wave is best represented by
-The frequency spectrum of the composite wave is best represented by
(Multiple Choice)
4.8/5  (33)
(33)
The fundamental frequency of a vibrating string is 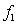 . If the tension in the string is quadrupled while the linear density is held constant, the fundamental frequency becomes
. If the tension in the string is quadrupled while the linear density is held constant, the fundamental frequency becomes
(Multiple Choice)
4.8/5  (33)
(33)
On a standing-wave pattern, the distance between two consecutive nodes is d. The wavelength is
(Multiple Choice)
4.8/5  (43)
(43)
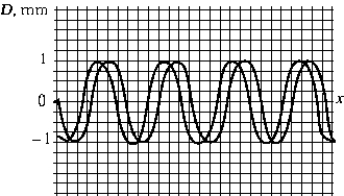 The figure shows two waves traveling in the positive-x direction. The phase difference between these two waves is closest to
The figure shows two waves traveling in the positive-x direction. The phase difference between these two waves is closest to
(Multiple Choice)
4.8/5  (42)
(42)
Two speakers face each other at a distance of 1 m and are driven by a common audio oscillator. A first minimum in sound intensity is found 16.1 cm from the midpoint. If the velocity of sound is 330 m/s, find the frequency of the oscillator.
(Multiple Choice)
4.7/5  (42)
(42)
The electronic music synthesizer is based on the results of
(Multiple Choice)
4.8/5  (40)
(40)
The wave function y(x,t) for a standing wave on a string fixed at both ends is given by y(x,t) = 0.080 sin 6.0x cos 600t where the units are SI. The wavelength of this wave is
(Multiple Choice)
4.9/5  (35)
(35)
Showing 41 - 60 of 125
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)