Exam 6: Analyzing Accumulated Change: Integrals in Action
Exam 1: Ingredients of Change: Functions an Limits50 Questions
Exam 2: Describing Change: Rates47 Questions
Exam 3: Determining Change: Derivatives48 Questions
Exam 4: Analyzing Change: Applications of Derivatives50 Questions
Exam 5: Accumulating Change: Limits of Sums and the Definite Integral50 Questions
Exam 6: Analyzing Accumulated Change: Integrals in Action51 Questions
Exam 7: Ingredients of Multivariable Change: Models, Graphs, Rates46 Questions
Exam 8: Analyzing Multivariable Change: Optimization50 Questions
Select questions type
In 1956, AT&T laid its first underwater phone line. By 1996, AT&T Submarine Systems, the division of AT&T that installs and maintains undersea communication lines, had seven cable ships and 1000 workers. On October 5, 1996, AT&T announced that it was seeking a buyer for its Submarine Systems division. The Submarine Systems division of AT&T was posting a profit of $850 million per year. If a prospective bidder considered that over a 25-year period, profits of the division would grow by 10% per year (after which it would be obsolete) and that profits could be reinvested at an annual return of 20%, what would the prospective bidder have considered to be the 25-year present value of its Submarine Systems division? Assume a continuous stream and round your answer to the nearest billion dollars. You may use technology to calculate the answer.
(Multiple Choice)
4.8/5  (27)
(27)
The demand for circus tickets can be modeled as 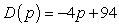 hundred tickets where p is the price (in dollars) of a ticket. According to the model, at what price will consumers no longer purchase circus tickets?
hundred tickets where p is the price (in dollars) of a ticket. According to the model, at what price will consumers no longer purchase circus tickets?
(Multiple Choice)
4.8/5  (40)
(40)
For the first 9 months of life, the average weight w, in pounds, of a certain breed of dog increases at a rate that is inversely proportional to time t, in months. A 1-month-old puppy's weight is changing at a rate of 8 pounds per month, and a 9-month-old puppy weighs 90 pounds. Write a differential equation describing the rate of change of the weight of the puppy.
(Multiple Choice)
4.8/5  (34)
(34)
Evaluate the improper integral if it converges, or state that it diverges. 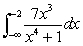
(Multiple Choice)
4.8/5  (30)
(30)
The daily demand for beef can be modeled by 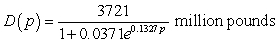 where the price for beef is p dollars per pound. Like-wise, the supply for beef can be modeled by
where the price for beef is p dollars per pound. Like-wise, the supply for beef can be modeled by 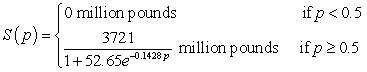 where the price for beef is p dollars per pound. How much beef is supplied when the price is $3.50 per pound? Round your answer to the nearest million pounds.
where the price for beef is p dollars per pound. How much beef is supplied when the price is $3.50 per pound? Round your answer to the nearest million pounds.
(Multiple Choice)
4.9/5  (32)
(32)
The demand for train sets can be modeled as 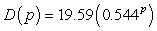 train sets where p is the price (in dollars) of a train set. For what prices is demand elastic?
train sets where p is the price (in dollars) of a train set. For what prices is demand elastic?
(Multiple Choice)
4.9/5  (36)
(36)
Barometric pressure p (measured in inches of mercury) decreases with respect to altitude a (measured in feet) at a rate that is directly proportional to the altitude. Assume the constant of proportionality is 0.003. Write a differential equation representing the rate of change of barometric pressure.
(Multiple Choice)
4.9/5  (36)
(36)
Evaluate the improper integral if it converges, or state that it diverges. 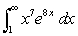
(Multiple Choice)
4.8/5  (32)
(32)
The average quantity of sculptures that consumers will demand can be modeled as 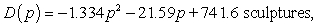 and the average quantity that producers will supply can be modeled as
and the average quantity that producers will supply can be modeled as 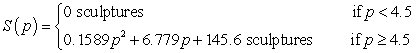 where the market price is p hundred dollars per sculpture. By how much will demand exceed supply at a price of $500 per sculpture?
where the market price is p hundred dollars per sculpture. By how much will demand exceed supply at a price of $500 per sculpture?
(Multiple Choice)
4.9/5  (31)
(31)
The average quantity of sculptures that consumers will demand can be modeled as 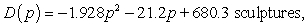 and the average quantity that producers will supply can be modeled as
and the average quantity that producers will supply can be modeled as 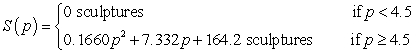 where the market price is p hundred dollars per sculpture. Determine the total social gain when sculptures are sold at the equilibrium price. Round your answer to the nearest dollar.
where the market price is p hundred dollars per sculpture. Determine the total social gain when sculptures are sold at the equilibrium price. Round your answer to the nearest dollar.
(Multiple Choice)
4.8/5  (34)
(34)
Find a general solution for the following differential equation: 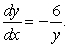
(Multiple Choice)
4.9/5  (37)
(37)
Showing 41 - 51 of 51
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)