Exam 10: Infinite Series
Exam 1: Preliminaries101 Questions
Exam 2: Limits and Continuity105 Questions
Exam 3: Differentiation116 Questions
Exam 4: Applications of the Derivative118 Questions
Exam 5: Integration129 Questions
Exam 6: Applications of the Definite Integral85 Questions
Exam 7: Exponentials, Logarithms and Other Transcendental Functions66 Questions
Exam 8: Integration Techniques123 Questions
Exam 9: First-Order Differential Equations72 Questions
Exam 10: Infinite Series111 Questions
Exam 11: Parametric Equations and Polar Coordinates129 Questions
Exam 12: Vectors and the Geometry of Space107 Questions
Exam 13: Vector-Valued Functions103 Questions
Exam 14: Functions of Several Variables and Partial Differentiation112 Questions
Exam 15: Multiple Integrals92 Questions
Exam 16: Vector Calculus67 Questions
Exam 17: Second Order Differential Equations38 Questions
Select questions type
Determine all values of c such that the series converges. 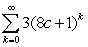
Free
(Multiple Choice)
4.9/5  (33)
(33)
Correct Answer:
C
Determine convergence or divergence of the series. 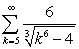
Free
(Essay)
4.9/5  (34)
(34)
Correct Answer:
Since 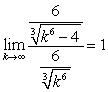 and the series
and the series 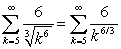 is a convergent p-series, the given series converges by the Limit Comparison Test.
is a convergent p-series, the given series converges by the Limit Comparison Test.
Estimate the error in using 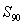 to approximate the sum of
to approximate the sum of 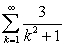 . Show all your work.
. Show all your work.
Free
(Essay)
4.8/5  (28)
(28)
Correct Answer:
Answers may vary.
Let 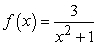 . Since
. Since 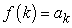 for all
for all 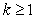 , and since
, and since 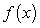 is decreasing and non-zero for all
is decreasing and non-zero for all 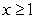 , then we can use the Error Estimate Theorem for the Integral Test.
, then we can use the Error Estimate Theorem for the Integral Test. 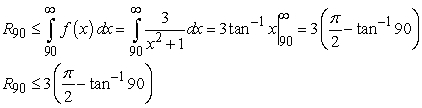
Use a known Taylor polynomial with 3 non-zero terms to estimate the value of 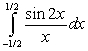 .
.
(Multiple Choice)
4.8/5  (32)
(32)
Estimate the error in using 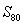 to approximate the sum of
to approximate the sum of 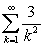 . Show all your work.
. Show all your work.
(Essay)
4.8/5  (44)
(44)
Determine if 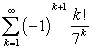 is absolutely convergent, conditionally convergent or divergent.
is absolutely convergent, conditionally convergent or divergent.
(Multiple Choice)
4.8/5  (26)
(26)
Find the Taylor series about c = 1 and its interval of convergence. 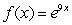
(Multiple Choice)
4.7/5  (37)
(37)
Write a formula that produces the given terms of the sequence. 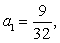
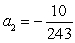 ,
, 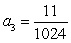 ,
, 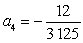
(Multiple Choice)
5.0/5  (40)
(40)
Suppose that the total salary of all the employees at a factory in a certain city is $350,000. Of this salary, 80% is spent in the city. Of the money spent in the city, 80% is again spent in the city. If this continues indefinitely, how much total money is spent in the city, that is, how much of an effect does the original total salary have on the local economy?
(Multiple Choice)
4.8/5  (26)
(26)
Determine how many terms are needed to estimate 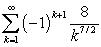 to within 0.001.
to within 0.001.
(Multiple Choice)
4.7/5  (39)
(39)
Determine whether the series is absolutely convergent, conditionally convergent, or divergent. 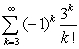
(Multiple Choice)
4.9/5  (36)
(36)
Determine if 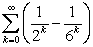 converges or diverges. If convergent, find the sum of the series.
converges or diverges. If convergent, find the sum of the series.
(Multiple Choice)
4.9/5  (43)
(43)
Graph 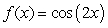 about c =
about c = 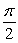 and the Taylor polynomials for n = 3 and n = 6.
and the Taylor polynomials for n = 3 and n = 6. 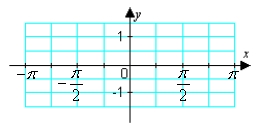
(Multiple Choice)
4.7/5  (31)
(31)
Showing 1 - 20 of 111
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)