Exam 14: Functions of Several Variables and Partial Differentiation
Exam 1: Preliminaries101 Questions
Exam 2: Limits and Continuity105 Questions
Exam 3: Differentiation116 Questions
Exam 4: Applications of the Derivative118 Questions
Exam 5: Integration129 Questions
Exam 6: Applications of the Definite Integral85 Questions
Exam 7: Exponentials, Logarithms and Other Transcendental Functions66 Questions
Exam 8: Integration Techniques123 Questions
Exam 9: First-Order Differential Equations72 Questions
Exam 10: Infinite Series111 Questions
Exam 11: Parametric Equations and Polar Coordinates129 Questions
Exam 12: Vectors and the Geometry of Space107 Questions
Exam 13: Vector-Valued Functions103 Questions
Exam 14: Functions of Several Variables and Partial Differentiation112 Questions
Exam 15: Multiple Integrals92 Questions
Exam 16: Vector Calculus67 Questions
Exam 17: Second Order Differential Equations38 Questions
Select questions type
Find all first-order partial derivatives. 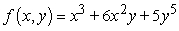
Free
(Multiple Choice)
4.9/5  (27)
(27)
Correct Answer:
C
Match the surface to its density plot. 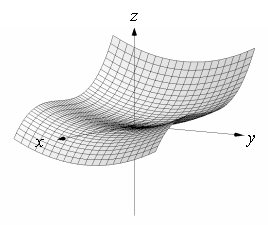
Free
(Multiple Choice)
4.9/5  (36)
(36)
Correct Answer:
C
Compute the directional derivative of 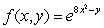 at
at 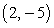 in the direction of
in the direction of 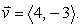
Free
(Multiple Choice)
4.8/5  (37)
(37)
Correct Answer:
D
Determine all points at which the given function is continuous. 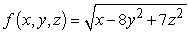
(Multiple Choice)
4.7/5  (32)
(32)
Show that the function 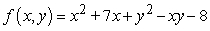 has exactly one critical point, which is an absolute minimum.
has exactly one critical point, which is an absolute minimum.
(Essay)
4.7/5  (24)
(24)
Find the gradient of the given function at the indicated point. 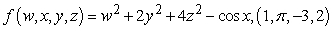
(Multiple Choice)
4.9/5  (30)
(30)
Use polar coordinates to find the indicated limit, if it exists. Note that 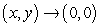 is equivalent to
is equivalent to 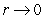 .
. 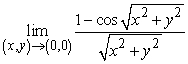
(Multiple Choice)
4.7/5  (33)
(33)
State the chain rule for finding 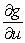 for the general composite function involving
for the general composite function involving 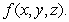
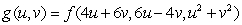
(Multiple Choice)
4.9/5  (34)
(34)
Suppose that on a fixed budget of $400 you buy x units of product A purchased at $20 apiece and y units of product B purchased at $20 apiece. For the utility function 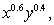 find x and y that maximize the utility function.
find x and y that maximize the utility function.
(Multiple Choice)
4.8/5  (35)
(35)
Use Lagrange multipliers to find the maximum and minimum of the function 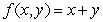 subject to
subject to 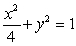 .
.
(Essay)
4.8/5  (39)
(39)
In the contour plot, the locations of two local extrema and one saddle point are visible. Identify these critical points. 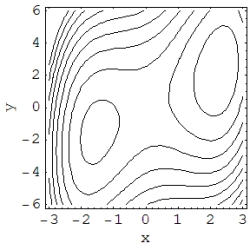
(Essay)
4.8/5  (37)
(37)
Use a graphing utility to sketch the graph of 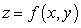 . Use the viewpoint
. Use the viewpoint 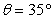 and
and 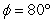 (see figure).
(see figure). 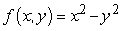
(Multiple Choice)
4.9/5  (35)
(35)
Use implicit differentiation to find 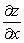 and
and 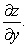 Assume that the equation defines z as a differentiable function near each
Assume that the equation defines z as a differentiable function near each 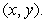
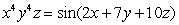
(Essay)
4.8/5  (35)
(35)
Numerically approximate all critical points. Classify each. 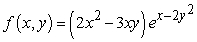
(Multiple Choice)
4.9/5  (35)
(35)
Showing 1 - 20 of 112
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)