Exam 8: Calculus of Several Variables
Exam 1: Preliminaries205 Questions
Exam 2: Functions, Limits and the Derivative269 Questions
Exam 3: Differentiation330 Questions
Exam 4: Applications of the Derivative182 Questions
Exam 5: Exponential and Logarithmic Functions278 Questions
Exam 6: Integration314 Questions
Exam 7: Additional Topics in Integration250 Questions
Exam 8: Calculus of Several Variables206 Questions
Select questions type
An open rectangular box having a volume of 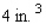 is to be constructed from a tin sheet. Find the dimensions of such a box if the amount of material used in its construction is to be minimal. Hint: Let the dimensions of the box be x by y by z. Then, xyz = 108 and the amount of material used is given by S = xy + 2yz + 2xz. Show that
is to be constructed from a tin sheet. Find the dimensions of such a box if the amount of material used in its construction is to be minimal. Hint: Let the dimensions of the box be x by y by z. Then, xyz = 108 and the amount of material used is given by S = xy + 2yz + 2xz. Show that 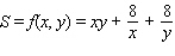 Minimize f(x, y)
Minimize f(x, y)
(Multiple Choice)
4.9/5  (40)
(40)
Use a double integral to find the volume of the solid shown in the figure. 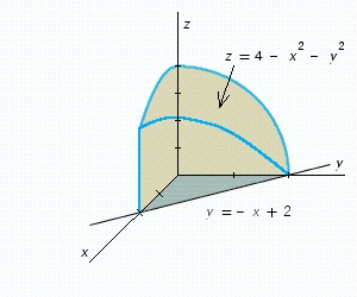
(Essay)
4.8/5  (29)
(29)
A closed rectangular box having a volume of 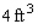 is to be constructed. If the material for the sides costs
is to be constructed. If the material for the sides costs 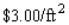 and the material for the top and bottom costs
and the material for the top and bottom costs 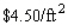 , find the dimensions of the box that can be constructed with minimum cost.
, find the dimensions of the box that can be constructed with minimum cost.
(Multiple Choice)
4.9/5  (36)
(36)
The following data, compiled by the superintendent of schools in a large metropolitan area, shows the average SAT verbal scores of high school seniors during the 5 years since the district implemented its "back-to-basics" program.  Determine the equation of the least-squares line for these data. Use the result obtained to predict the average SAT verbal score of high school seniors 2 years from now (x = 7). Please round your answer to the nearest whole number.
Determine the equation of the least-squares line for these data. Use the result obtained to predict the average SAT verbal score of high school seniors 2 years from now (x = 7). Please round your answer to the nearest whole number.
(Multiple Choice)
4.8/5  (33)
(33)
Find the average value of the function 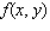 over the plane region
over the plane region 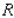 .
. 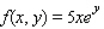 and
and  is the triangle with vertices
is the triangle with vertices 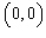 ,
, 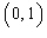 and
and 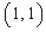 .
.
(Essay)
4.9/5  (32)
(32)
The Social Security (FICA) wage base (in thousands of dollars) from 1996 to 2001 is given in the following table:  Find an equation of the least-squares line for these data. (Let x = 1 represent the year 1996.) Please round the coefficients in your equation to three decimal places. Use the result to estimate the FICA wage base in the year 2007.
Find an equation of the least-squares line for these data. (Let x = 1 represent the year 1996.) Please round the coefficients in your equation to three decimal places. Use the result to estimate the FICA wage base in the year 2007.
(Multiple Choice)
4.9/5  (36)
(36)
An open rectangular box is to be constructed from material that costs 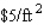 for the bottom and
for the bottom and 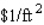 for its sides. Find the dimensions of the box of greatest volume that can be constructed for
for its sides. Find the dimensions of the box of greatest volume that can be constructed for 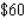 .
.
(Multiple Choice)
4.9/5  (40)
(40)
Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. The least-squares line must pass through at least one data point.
(Multiple Choice)
4.8/5  (45)
(45)
Evaluate the double integral 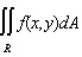 for the given function f(x, y) and the region R.
f(x, y) = 4x + 8y; R is bounded by x = 1, x = 3, y = 0 and y = x + 1.
for the given function f(x, y) and the region R.
f(x, y) = 4x + 8y; R is bounded by x = 1, x = 3, y = 0 and y = x + 1.
(Essay)
4.8/5  (27)
(27)
Sketch the level curves of the function corresponding to the given values of z. f(x, y) = xy; z = - 2, - 1, 1, 2
(Multiple Choice)
4.7/5  (24)
(24)
In a survey it was determined that the demand equation for VCRs is given by 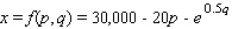 The demand equation for blank VCR tapes is given by
The demand equation for blank VCR tapes is given by 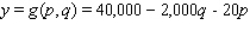 where
where 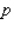 and
and 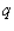 denote the unit prices, respectively, and
denote the unit prices, respectively, and 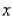 and
and 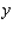 denote the number of VCRs and the number of blank VCR tapes demanded each week. Determine whether these two products are substitute, complementary, or neither.
denote the number of VCRs and the number of blank VCR tapes demanded each week. Determine whether these two products are substitute, complementary, or neither.
(Multiple Choice)
4.7/5  (43)
(43)
The volume V (in liters) of a certain mass of gas is related to its pressure P (in millimeters of mercury) and its temperature T (in degrees Kelvin) by the law 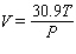 Compute
Compute 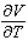 and
and 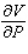 when T = 260 and P = 700.
when T = 260 and P = 700.
(Multiple Choice)
5.0/5  (35)
(35)
Find the second order partial derivative of the following function. Show that the mixed partial derivative 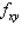 and
and 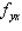 are equal.
are equal. 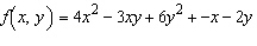
(Multiple Choice)
4.7/5  (41)
(41)
Showing 61 - 80 of 206
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)