Exam 8: Calculus of Several Variables
Exam 1: Preliminaries205 Questions
Exam 2: Functions, Limits and the Derivative269 Questions
Exam 3: Differentiation330 Questions
Exam 4: Applications of the Derivative182 Questions
Exam 5: Exponential and Logarithmic Functions278 Questions
Exam 6: Integration314 Questions
Exam 7: Additional Topics in Integration250 Questions
Exam 8: Calculus of Several Variables206 Questions
Select questions type
A closed rectangular box having a volume of 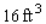 is to be constructed. If the material for the sides costs
is to be constructed. If the material for the sides costs 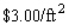 and the material for the top and bottom costs
and the material for the top and bottom costs 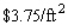 , find the dimensions of the box that can be constructed with minimum cost.
, find the dimensions of the box that can be constructed with minimum cost.
(Essay)
5.0/5  (28)
(28)
Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. 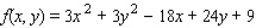
(Multiple Choice)
4.8/5  (42)
(42)
Evaluate the double integral 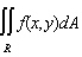 for the given function f(x, y) and the region R.
f(x, y) = 2y + 3x; R is the rectangle defined by
for the given function f(x, y) and the region R.
f(x, y) = 2y + 3x; R is the rectangle defined by 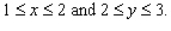
(Essay)
4.9/5  (44)
(44)
Find the average value of the given function
f(x, y)
over the plane region R. 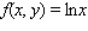 ; R is the region bounded by the graph of y = 6x and y = 0 from x = 1 to x = 5.
; R is the region bounded by the graph of y = 6x and y = 0 from x = 1 to x = 5.
(Essay)
4.8/5  (28)
(28)
Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. 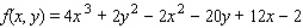
(Multiple Choice)
4.9/5  (24)
(24)
The population density of a certain city is given by the function 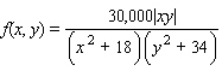 where the origin (0, 0) gives the location of the government center. Find the population inside the rectangular area described by
where the origin (0, 0) gives the location of the government center. Find the population inside the rectangular area described by 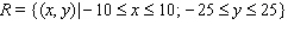
(Multiple Choice)
4.9/5  (33)
(33)
Evaluate the first partial derivatives of the function at the given point. 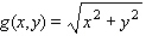 ;
; 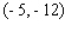
(Multiple Choice)
4.9/5  (36)
(36)
A building in the shape of a rectangular box is to have a volume of 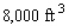 (see the figure). It is estimated that the annual heating and cooling costs will be $2/square foot for the top, $4/square foot for the front and back, and $2/square foot for the sides. Find the dimensions of the building that will result in a minimal annual heating and cooling cost. What is the minimal annual heating and cooling cost(C)?
(see the figure). It is estimated that the annual heating and cooling costs will be $2/square foot for the top, $4/square foot for the front and back, and $2/square foot for the sides. Find the dimensions of the building that will result in a minimal annual heating and cooling cost. What is the minimal annual heating and cooling cost(C)? 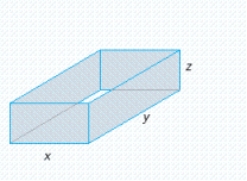
(Essay)
4.9/5  (35)
(35)
Steel has been playing a decreasing role in the manufacture of beverage cans in the United States. The use of bimetallic cans has been dwindling, whereas the use of all-aluminum cans has been growing steadily. The accompanying table gives the production (in billions) of all-aluminum cans over the period from 1975 through 1989:  Find an equation of the least-squares line for these data. (Let x = 1 represent the year 1975.) Please round the coefficients in your equation to three decimal places. Use the result to estimate the number of cans produced in 1993, assuming the trend continued.
Find an equation of the least-squares line for these data. (Let x = 1 represent the year 1975.) Please round the coefficients in your equation to three decimal places. Use the result to estimate the number of cans produced in 1993, assuming the trend continued.
(Multiple Choice)
4.8/5  (39)
(39)
Use a double integral to find the volume of the solid shown in the figure. 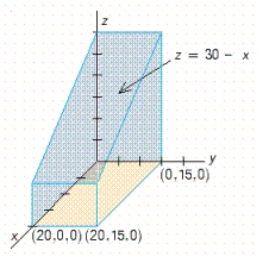
(Multiple Choice)
4.8/5  (32)
(32)
A building in the shape of a rectangular box is to have a volume of 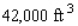 (see the figure). It is estimated that the annual heating and cooling costs will be $2/square foot for the top, $7/square foot for the front and back, and $6/square foot for the sides. Find the dimensions of the building that will result in a minimal annual heating and cooling cost. What is the minimal annual heating and cooling cost(C)?
(see the figure). It is estimated that the annual heating and cooling costs will be $2/square foot for the top, $7/square foot for the front and back, and $6/square foot for the sides. Find the dimensions of the building that will result in a minimal annual heating and cooling cost. What is the minimal annual heating and cooling cost(C)? 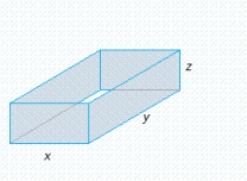
(Multiple Choice)
4.9/5  (33)
(33)
Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false.
If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then ![Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where](https://storage.examlex.com/TB6026/11eaa8b1_d981_786c_b1b6_f3f19210a87b_TB6026_11.jpg) where
where ![Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where](https://storage.examlex.com/TB6026/11eaa8b1_d981_786d_b1b6_296c145eb06d_TB6026_11.jpg)
(Essay)
4.7/5  (36)
(36)
Evaluate the double integral 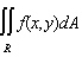 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R. 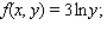 R is the rectangle defined by
R is the rectangle defined by 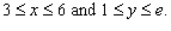
(Multiple Choice)
4.7/5  (30)
(30)
The Country Workshop's total weekly profit (in dollars) realized in manufacturing and selling its rolltop desks is given by the profit function 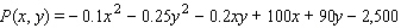 where
where 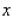 stands for the number of finished units and
stands for the number of finished units and 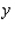 stands for the number of unfinished units manufactured and sold each week. Find the average weekly profit if the number of finished units manufactured and sold varies between
stands for the number of unfinished units manufactured and sold each week. Find the average weekly profit if the number of finished units manufactured and sold varies between  and
and 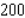 and the number of unfinished units varies between
and the number of unfinished units varies between 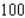 and
and 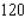 per week. Please round your answer to the nearest dollar, if necessary.
per week. Please round your answer to the nearest dollar, if necessary.
(Multiple Choice)
5.0/5  (38)
(38)
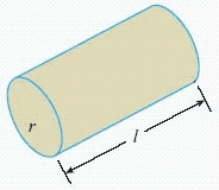
Postal regulations specify that a parcel sent by parcel post may have a combined length and girth of no more than 105 in. Find the dimensions of the cylindrical package of greatest volume that may be sent through the mail. What is the volume of such a package? Hint: The length plus the girth is 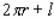 , and the volume is
, and the volume is 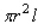 .
. 
(Multiple Choice)
4.7/5  (31)
(31)
Find the maximum and minimum values of the function 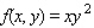 subject to the constraint
subject to the constraint 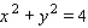 .
.
(Multiple Choice)
4.7/5  (35)
(35)
The estimated number of computers (in millions) connected to the Internet in Europe from 1998 through 2002 is summarized in the accompanying table:  (Here, x = 0 corresponds to the beginning of 1998.)
Find an equation of the least-squares line for these data. Use the result to estimate the projected number of computers connected to the Internet in Europe at the beginning of 2004, assuming the trend continues.
(Here, x = 0 corresponds to the beginning of 1998.)
Find an equation of the least-squares line for these data. Use the result to estimate the projected number of computers connected to the Internet in Europe at the beginning of 2004, assuming the trend continues.
(Multiple Choice)
4.8/5  (33)
(33)
Showing 81 - 100 of 206
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)