Exam 8: Calculus of Several Variables
Exam 1: Preliminaries205 Questions
Exam 2: Functions, Limits and the Derivative269 Questions
Exam 3: Differentiation330 Questions
Exam 4: Applications of the Derivative182 Questions
Exam 5: Exponential and Logarithmic Functions278 Questions
Exam 6: Integration314 Questions
Exam 7: Additional Topics in Integration250 Questions
Exam 8: Calculus of Several Variables206 Questions
Select questions type
The productivity of a South American country is given by the function 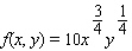 when x units of labor and y units of capital are used. What is the marginal productivity of labor and what is the marginal productivity of capital when the amounts expended on labor and capital are 288 units and 18 units, respectively? Should the government encourage capital investment rather than increased expenditure on labor at this time in order to increase the country's productivity? Please answer yes or no.
when x units of labor and y units of capital are used. What is the marginal productivity of labor and what is the marginal productivity of capital when the amounts expended on labor and capital are 288 units and 18 units, respectively? Should the government encourage capital investment rather than increased expenditure on labor at this time in order to increase the country's productivity? Please answer yes or no.
(Multiple Choice)
4.9/5  (37)
(37)
Find the second-order partial derivatives of the function. 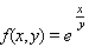
(Multiple Choice)
4.9/5  (30)
(30)
Find the equation of the least-squares line for the given data. Draw a scatter diagram for the given data and graph the least-squares line. 
(Multiple Choice)
4.8/5  (38)
(38)
A formula used by meteorologists to calculate the wind chill temperature (the temperature that you feel in still air that is the same as the actual temperature when the presence of wind is taken into consideration) is 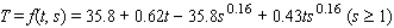 where t is the actual air temperature in
where t is the actual air temperature in 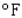 and S is the wind speed in mph. What is the wind chill temperature when the actual air temperature is
and S is the wind speed in mph. What is the wind chill temperature when the actual air temperature is 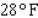 and the wind speed is 15 mph (
and the wind speed is 15 mph ( 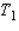 )? Please round the answer to the nearest
)? Please round the answer to the nearest 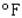 If the temperature is
If the temperature is 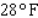 , by how much approximately will the wind chill temperature change if the wind speed increases from 15 mph to 16 mph (
, by how much approximately will the wind chill temperature change if the wind speed increases from 15 mph to 16 mph ( 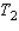 )? Please round the answer to the nearest tenth.
)? Please round the answer to the nearest tenth.
(Multiple Choice)
4.9/5  (36)
(36)
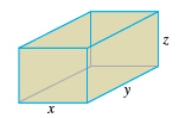
An open rectangular box having a surface area of 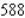
 is to be constructed from a tin sheet.Find the diamensions of the box if the volume of the box is to be as large as possible. What is the maximum volume? Hint : Let the diamentions of the box be
is to be constructed from a tin sheet.Find the diamensions of the box if the volume of the box is to be as large as possible. What is the maximum volume? Hint : Let the diamentions of the box be 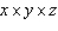 (see the figure as follows). Then the surface area is
(see the figure as follows). Then the surface area is 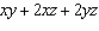 and its volume is
and its volume is 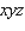 .
. 
(Multiple Choice)
4.8/5  (32)
(32)
Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. 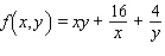
(Multiple Choice)
4.8/5  (40)
(40)
Evaluate the double integral 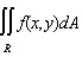 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R. 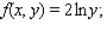 R is the rectangle defined by
R is the rectangle defined by 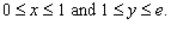
(Short Answer)
4.9/5  (24)
(24)
Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. 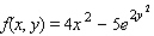
(Multiple Choice)
4.7/5  (34)
(34)
Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. 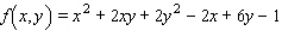
(Multiple Choice)
4.9/5  (29)
(29)
Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. 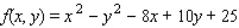
(Multiple Choice)
4.8/5  (34)
(34)
Evaluate the double integral 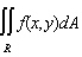 for the given function f(x, y) and the region R. f(x, y) = 6x + 12y; R is bounded by x = 1, x = 3, y = 0 and y = x + 1.
for the given function f(x, y) and the region R. f(x, y) = 6x + 12y; R is bounded by x = 1, x = 3, y = 0 and y = x + 1.
(Multiple Choice)
4.9/5  (37)
(37)
Evaluate the double integral 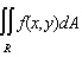 for the given function f(x, y) and the region R. f(x, y) = 2y + x; R is the rectangle defined by
for the given function f(x, y) and the region R. f(x, y) = 2y + x; R is the rectangle defined by 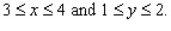
(Multiple Choice)
4.9/5  (30)
(30)
Evaluate the first partial derivatives of the function at the given point. 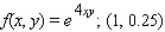
(Multiple Choice)
4.8/5  (29)
(29)
Find the volume of the solid bounded above by the surface
z = f(x, y)
and below by the plane region R. 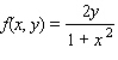 ; R is the region bounded by
; R is the region bounded by 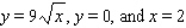 .
.
(Essay)
4.8/5  (27)
(27)
Find the maximum and minimum values of the function 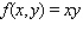 subject to the constraint
subject to the constraint 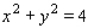 .
.
(Multiple Choice)
4.9/5  (44)
(44)
Use a double integral to find the volume of the solid shown in the figure. 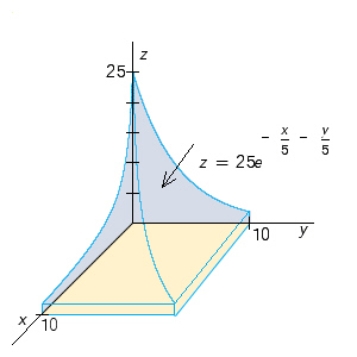
(Multiple Choice)
4.7/5  (28)
(28)
Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. 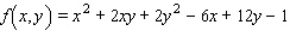 Find the critical point(s) of the function.
Find the point(s) of maximum.
Find the point(s) of minimum.
Find the relative extrema of the function.
Find the critical point(s) of the function.
Find the point(s) of maximum.
Find the point(s) of minimum.
Find the relative extrema of the function.
(Essay)
4.8/5  (31)
(31)
Showing 121 - 140 of 206
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)