Exam 12: Linear Regression and Correlation

i. Trying to predict weekly sales with a standard error of estimate of $1,955, we would conclude that 68 percent of the predictions would not be off more than $1,955, 95 percent would not be off by more $3,910, and 99.7 percent would not be off by more than $5,865. ii. Approximately 95% of the values lie within two standard errors of the regression line. iii. The smaller the sample, the smaller the possible error as measured by the standard error of estimate.

High school students were interested in a teacher's claim that the longer the length of time (hours) that a student studies for a test, the higher the test score. The students collected the data and the teacher did the regression analysis with the following results. 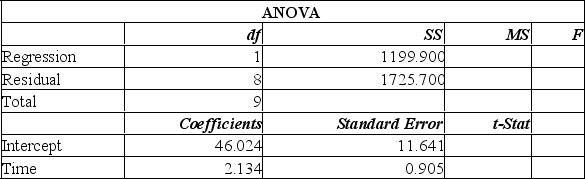Determine the linear regression equation.

Data is collected from 20 sales people in order to verify that the more contacts made with potential clients, the greater the sales volume. The Mega Stat printout is shown below. 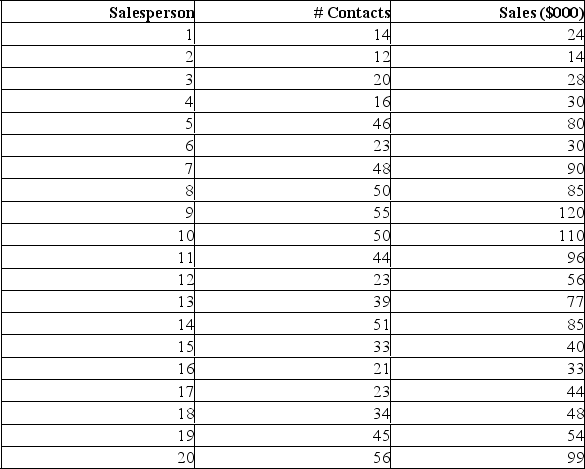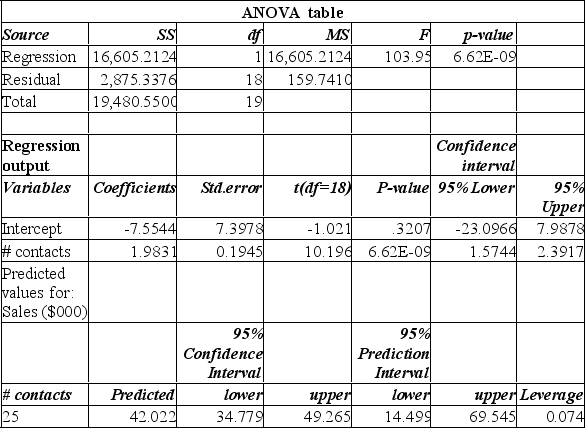Analyzing this printout we can determine:

i. A t test is used to test the significance of the coefficient of correlation. ii. When testing the strength of the relationship between two variables, the alternate hypothesis is: H₀: $\rho$ $\neq$ 0. iii. Suppose a sample of 15 homes recently sold in your area is obtained. The correlation between the area of the home, in square feet, and the selling price is 0.40. We want to test the hypothesis that the correlation in the population is zero versus the alternate that it is greater than zero. You determine that the rejection region should fall in the lower tail if this is a one-tailed test and we use a 0.01 significance level.

The regression equation is:

i. A coefficient of correlation close to 0 (say, 0.08) shows that the relationship between two variables is quite weak. ii. If the coefficient of correlation is 0.68, the coefficient of determination is 0.4624. iii. The standard error of estimate measures the accuracy of our prediction.

Suppose the least squares regression equation is Y' = 1202 + 1,133X. When X = 3, what does Y' equal?

Data is collected from 20 sales people in order to verify that the more contacts made with potential clients, the greater the sales volume. The Mega Stat printout is shown below. 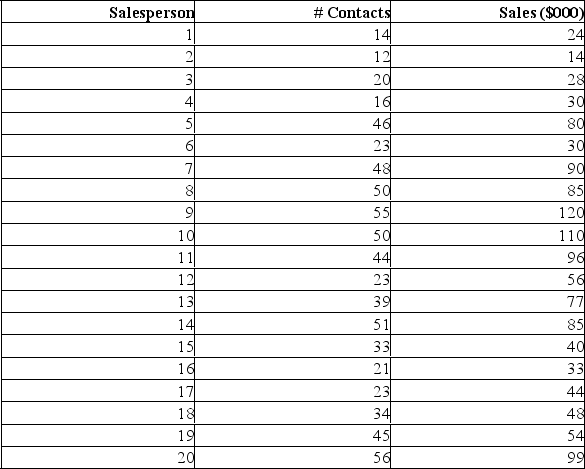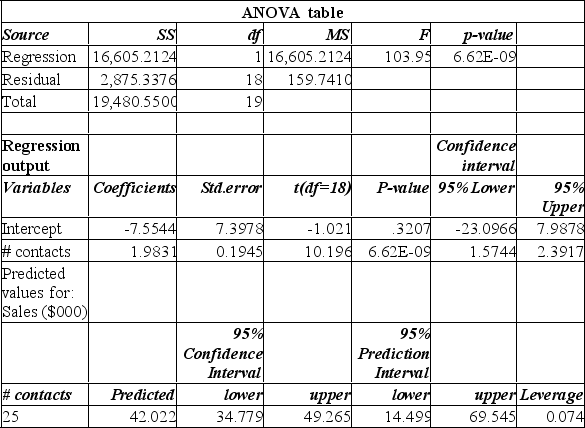Analyzing this printout, we can determine:

Which value of r indicates a stronger correlation than 0.40?

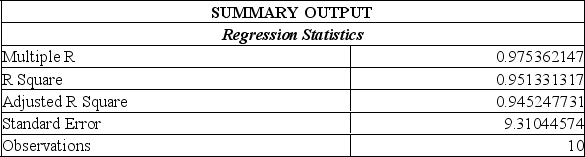
A sales manager for an advertising agency believes there is a relationship between the number of contacts and the amount of the sales. To verify this belief, the following data was collected: 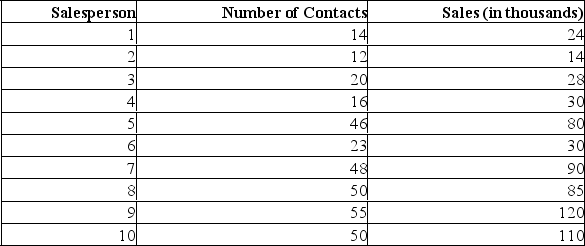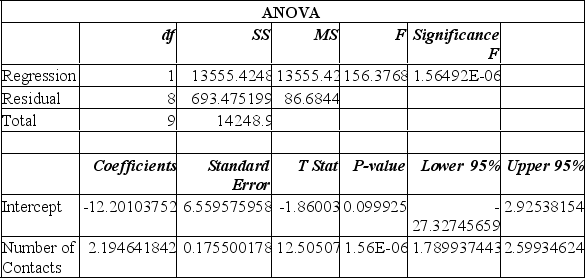The SS total is:

i. Perfect correlation means that the scatter diagram will appear as a straight line ii. If the coefficient of correlation is 0.80, the coefficient of determination is 0.64. iii. The coefficient of determination can assume values between 0% and 100%

High school students were interested in a teacher's claim that the longer the length of time (hours) that a student studies for a test, the higher the test score. The students collected the data and the teacher did the regression analysis with the following results. 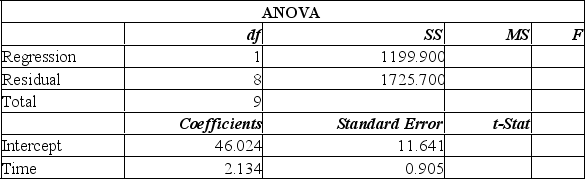If a student studies 10 hours, what is the predicted score?

Information was collected from employee records to determine whether there is an association between an employee's age and the number or workdays they miss. Excel results are summarized below: 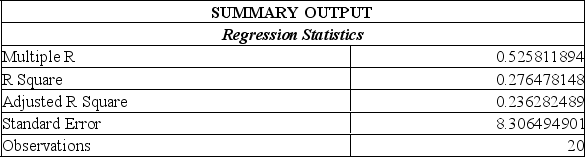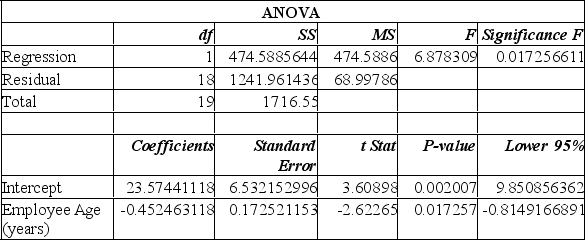From this printout you determine:

In the equation Y' = a + bX, what is Y'?

i. The technique used to measure the strength of the relationship between two sets of variables using the coefficient of correlation and the coefficient of determination is called regression analysis. ii. In order to visualize the form of the regression equation, we can draw a scatter diagram. iii. A line found using the is the best-fitting line because the sum of the squares of the vertical deviations between the actual and estimated values is minimized.

i. A coefficient of correlation close to 0 (say, 0.08) shows that the relationship between two variables is quite weak. ii. Coefficients of -0.91 and +0.91 have equal strength. iii. If the coefficient of correlation is 0.68, the coefficient of determination is 0.4624.

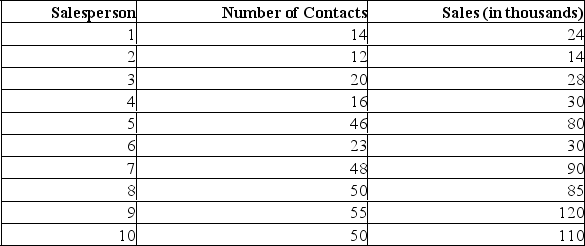
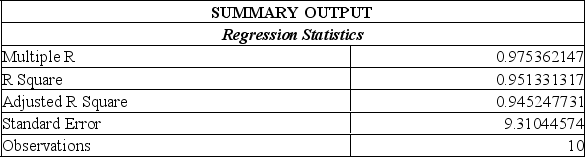
A sales manager for an advertising agency believes there is a relationship between the number of contacts and the amount of the sales. To verify this belief, the following data was collected: 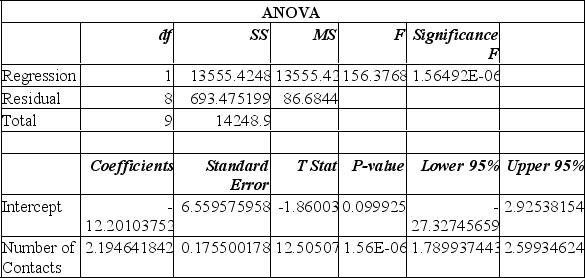What is the value of the standard error of estimate?

i. In order to visualize the form of the regression equation, we can draw a scatter diagram. ii. In regression analysis, the predicted value of Y' rarely agrees exactly with the actual Y value, i.e., we expect some prediction error. iii. The technique used to measure the strength of the relationship between two sets of variables using the coefficient of correlation and the coefficient of determination is called regression analysis.

Given the following five points: (-2,0), (-1,0), (0,1), (1,1), and (2,3). What is the Y intercept?

i. A coefficient of correlation close to 0 (say, 0.08) shows that the relationship between two variables is quite weak. ii. A coefficient of correlation of -0.96 indicates a very weak negative correlation. iii. If the coefficient of correlation is 0.68, the coefficient of determination is 0.4624.