Exam 9: Infinite Series
Exam 1: Preliminaries143 Questions
Exam 2: Limits and Continuity125 Questions
Exam 3: Differentiation150 Questions
Exam 4: Applications of the Derivative143 Questions
Exam 5: Integration154 Questions
Exam 6: Applications of the Definite Integral113 Questions
Exam 7: Integration Techniques95 Questions
Exam 8: First-Order Differential Equations72 Questions
Exam 9: Infinite Series111 Questions
Exam 10: Parametric Equations and Polar Coordinates129 Questions
Exam 11: Vectors and the Geometry of Space107 Questions
Exam 12: Vector-Valued Functions103 Questions
Exam 13: Functions of Several Variables and Partial Differentiation112 Questions
Exam 14: Multiple Integrals92 Questions
Exam 15: Vector Calculus67 Questions
Exam 16: Second Order Differential Equations38 Questions
Select questions type
Determine all values of c such that the series converges. 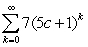
Free
(Multiple Choice)
5.0/5  (25)
(25)
Correct Answer:
C
Determine whether 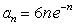 converges or diverges. Show all your work.
converges or diverges. Show all your work.
Free
(Essay)
4.9/5  (39)
(39)
Correct Answer:
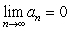 ; the limit exists, so the sequence converges.
; the limit exists, so the sequence converges.
Find the Fourier Series of 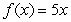 on the interval
on the interval 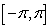 .
.
Free
(Multiple Choice)
4.8/5  (38)
(38)
Correct Answer:
B
Find the Taylor series about c = 4 and its interval of convergence. 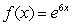
(Multiple Choice)
4.8/5  (29)
(29)
Find a power series representation of 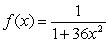 about
about 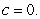 Determine the interval of convergence for the power series.
Determine the interval of convergence for the power series.
(Multiple Choice)
4.9/5  (38)
(38)
Find the power series representation (about c = 0), the radius of convergence, and the interval of convergence. 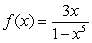
(Multiple Choice)
4.9/5  (35)
(35)
Determine whether the series is absolutely convergent, conditionally convergent, or divergent. 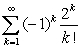
(Multiple Choice)
4.9/5  (33)
(33)
Use a known Taylor series to find the Taylor series about c = 0 for 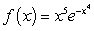 , and find its radius of convergence.
, and find its radius of convergence.
(Multiple Choice)
4.8/5  (33)
(33)
Determine if 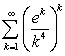 is absolutely convergent, conditionally convergent or divergent.
is absolutely convergent, conditionally convergent or divergent.
(Multiple Choice)
4.8/5  (37)
(37)
Determine whether the series is absolutely convergent, conditionally convergent, or divergent. 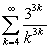
(Multiple Choice)
4.9/5  (36)
(36)
Estimate the error in the approximation of 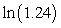 as a Taylor polynomial of degree 3 about c = 1. Show all your work.
as a Taylor polynomial of degree 3 about c = 1. Show all your work.
(Essay)
4.9/5  (36)
(36)
Estimate the error in using 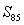 to approximate the sum of
to approximate the sum of 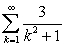 . Show all your work.
. Show all your work.
(Essay)
4.8/5  (38)
(38)
Determine if 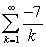 is absolutely convergent, conditionally convergent or divergent.
is absolutely convergent, conditionally convergent or divergent.
(Multiple Choice)
4.7/5  (28)
(28)
Use the even/odd properties of 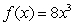 to predict (don't compute) whether the Fourier Series will contain only cosine terms, only sine terms or both.
to predict (don't compute) whether the Fourier Series will contain only cosine terms, only sine terms or both.
(Multiple Choice)
4.9/5  (43)
(43)
For 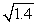 , estimate the number of terms needed in a Taylor polynomial with c = 1 to guarantee an accuracy of
, estimate the number of terms needed in a Taylor polynomial with c = 1 to guarantee an accuracy of 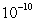 . Show all your work.
. Show all your work.
(Essay)
4.8/5  (42)
(42)
Estimate the error in using 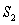 to approximate the sum of
to approximate the sum of 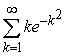 . Show all your work.
. Show all your work.
(Essay)
4.9/5  (36)
(36)
Use an appropriate Taylor series to approximate 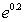 accurate to within 10-8.
accurate to within 10-8.
(Multiple Choice)
4.8/5  (32)
(32)
Showing 1 - 20 of 111
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)