Exam 5: Integration
Exam 1: Preliminaries143 Questions
Exam 2: Limits and Continuity125 Questions
Exam 3: Differentiation150 Questions
Exam 4: Applications of the Derivative143 Questions
Exam 5: Integration154 Questions
Exam 6: Applications of the Definite Integral113 Questions
Exam 7: Integration Techniques95 Questions
Exam 8: First-Order Differential Equations72 Questions
Exam 9: Infinite Series111 Questions
Exam 10: Parametric Equations and Polar Coordinates129 Questions
Exam 11: Vectors and the Geometry of Space107 Questions
Exam 12: Vector-Valued Functions103 Questions
Exam 13: Functions of Several Variables and Partial Differentiation112 Questions
Exam 14: Multiple Integrals92 Questions
Exam 15: Vector Calculus67 Questions
Exam 16: Second Order Differential Equations38 Questions
Select questions type
List the evaluation points corresponding to the midpoint of each subinterval, sketch the function and corresponding approximating rectangles and evaluate the corresponding Riemann sum. Round the sum to two decimal places. 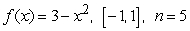
Free
(Essay)
4.8/5  (39)
(39)
Correct Answer:
The evaluation points are 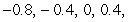 and 0.8.
and 0.8. 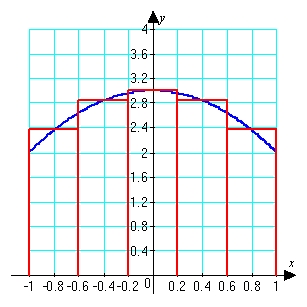 The Riemann sum is
The Riemann sum is 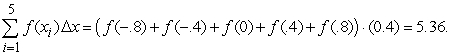

Use Part I of the Fundamental Theorem of Calculus to compute the integral exactly. 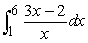
Free
(Multiple Choice)
4.9/5  (38)
(38)
Correct Answer:
B
Write out all terms and compute the sum. 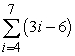
Free
(Multiple Choice)
4.9/5  (37)
(37)
Correct Answer:
B
Use the Midpoint Rule to estimate the value of the integral (obtain two digits of accuracy). 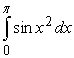
(Multiple Choice)
4.9/5  (32)
(32)
Determine the number of steps to guarantee an accuracy of 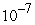 when approximating the integral using (a) the Trapezoidal Rule, (b) Midpoint Rule, and (c) Simpson's Rule.
when approximating the integral using (a) the Trapezoidal Rule, (b) Midpoint Rule, and (c) Simpson's Rule. 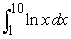
(Essay)
4.9/5  (33)
(33)
Use Riemann sums and a limit to compute the exact area under the curve. 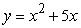 on
on 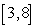
(Multiple Choice)
4.9/5  (31)
(31)
Find the area of the region bounded by 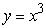 ,
, 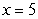 , the x-axis, and the y-axis.
, the x-axis, and the y-axis.
(Multiple Choice)
4.9/5  (37)
(37)
Use the given information about 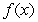 and its derivatives to determine whether (a) the Midpoint Rule would be exact, underestimate or overestimate the integeral (or if there's not enough information to tell). Repeat for (b) the Trapezoidal Rule and (c) Simpson's Rule.
and its derivatives to determine whether (a) the Midpoint Rule would be exact, underestimate or overestimate the integeral (or if there's not enough information to tell). Repeat for (b) the Trapezoidal Rule and (c) Simpson's Rule. 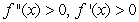
(Essay)
4.8/5  (37)
(37)
Use Riemann sums and a limit to compute the exact area under the curve. 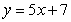 on
on 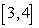
(Multiple Choice)
4.9/5  (40)
(40)
Use Part I of the Fundamental Theorem of Calculus to compute the integral exactly. 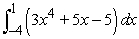
(Multiple Choice)
4.8/5  (29)
(29)
Use the properties of logarithms to rewrite the expression as a single term. 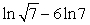
(Multiple Choice)
4.9/5  (33)
(33)
Make the indicated substitution for an unspecified function 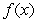 .
. 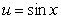 for
for 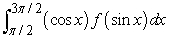
(Multiple Choice)
4.9/5  (29)
(29)
Evaluate the derivative using properties of logarithms where needed. 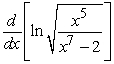
(Multiple Choice)
4.9/5  (25)
(25)
Showing 1 - 20 of 154
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)