Exam 6: Applications of the Definite Integral
Exam 1: Preliminaries143 Questions
Exam 2: Limits and Continuity125 Questions
Exam 3: Differentiation150 Questions
Exam 4: Applications of the Derivative143 Questions
Exam 5: Integration154 Questions
Exam 6: Applications of the Definite Integral113 Questions
Exam 7: Integration Techniques95 Questions
Exam 8: First-Order Differential Equations72 Questions
Exam 9: Infinite Series111 Questions
Exam 10: Parametric Equations and Polar Coordinates129 Questions
Exam 11: Vectors and the Geometry of Space107 Questions
Exam 12: Vector-Valued Functions103 Questions
Exam 13: Functions of Several Variables and Partial Differentiation112 Questions
Exam 14: Multiple Integrals92 Questions
Exam 15: Vector Calculus67 Questions
Exam 16: Second Order Differential Equations38 Questions
Select questions type
The annual increase in the value of a particular investment is 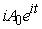 , where A0 is the amount of money initially invested, i is the interest rate expressed as a fraction or decimal (not a percent), and t is the time over which the investment has been growing. While the value of this investment increases over time as indicated, the amount of goods and services that money could buy does not increase as rapidly because of inflation. Inflation reduces the buying power of the investment annually by
, where A0 is the amount of money initially invested, i is the interest rate expressed as a fraction or decimal (not a percent), and t is the time over which the investment has been growing. While the value of this investment increases over time as indicated, the amount of goods and services that money could buy does not increase as rapidly because of inflation. Inflation reduces the buying power of the investment annually by 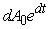 , where d is the rate of inflation expressed as a fraction. If i = 0.07/yr and d = 0.01/yr, how much additional buying power will an initial investment of $10,000 earn over ten years? Round to the nearest dollar.
, where d is the rate of inflation expressed as a fraction. If i = 0.07/yr and d = 0.01/yr, how much additional buying power will an initial investment of $10,000 earn over ten years? Round to the nearest dollar.
Free
(Multiple Choice)
4.8/5  (32)
(32)
Correct Answer:
B
Set up the integral for arc length and then approximate the integral with a numerical method. Round answers to four decimal places. 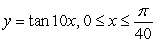
Free
(Essay)
4.9/5  (32)
(32)
Correct Answer:
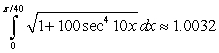
What is the total hydrostatic force on the walls of a cylindrical water tower 40' high and having a radius of 21'? [The density of water is 62.4 lbs/ft3.]
Free
(Multiple Choice)
4.9/5  (42)
(42)
Correct Answer:
C
A given sample of a particular polymer will have molecules with a range of molecular weights, MW. If the molecular weight pdf is 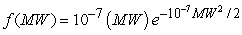 , what fraction of the molecules will have a molecular weight greater than 10,000?
, what fraction of the molecules will have a molecular weight greater than 10,000?
(Multiple Choice)
4.8/5  (33)
(33)
Let R be the region bounded by 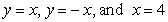 . Compute the volume of the solid formed by revolving R about y = 15.
. Compute the volume of the solid formed by revolving R about y = 15.
(Multiple Choice)
5.0/5  (40)
(40)
Find the volume of the solid formed by revolving the region bounded by 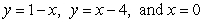 about x = 7.
about x = 7.
(Multiple Choice)
4.8/5  (28)
(28)
Given a certain amount of land potentially devoted to farming, one will first use the more fertile regions where production costs are lowest before using the less fertile regions. The consequence of this logical strategy is that the production costs increase as production increases. A certain landowner has enough land to produce 106 bushels of a particular crop, and the production costs, c, of the nth bushel is described with the equation 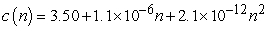 . If the market price is p for this particular crop, the profit for producing the nth bushel is
. If the market price is p for this particular crop, the profit for producing the nth bushel is 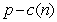 . If p = $5.50, how much total profit could the farmer expect to obtain by producing
. If p = $5.50, how much total profit could the farmer expect to obtain by producing 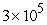 bushels.
bushels.
(Multiple Choice)
4.8/5  (35)
(35)
Find the volume of the solid with cross-sectional area 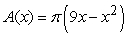 extending over the range
extending over the range 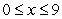 .
.
(Multiple Choice)
4.9/5  (42)
(42)
An anthill is in the shape formed by revolving the region bounded by 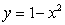 and the x-axis about the y-axis. A researcher removes a cylindrical core from the center of the hill. What should the radius be to give the researcher 15% of the dirt?
and the x-axis about the y-axis. A researcher removes a cylindrical core from the center of the hill. What should the radius be to give the researcher 15% of the dirt?
(Multiple Choice)
4.9/5  (29)
(29)
What is the maximum hydrostatic force a dam would need to withstand if it has the shape of a semicircle with a height (radius) of 20 feet? [The density of water is 62.4 lbs/ft3.]
(Multiple Choice)
4.9/5  (30)
(30)
Where is the center of mass of a region of uniform density bounded by 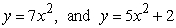 ?
?
(Multiple Choice)
4.8/5  (38)
(38)
Sketch the solid bounded by 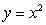 and the x-axis on the interval
and the x-axis on the interval 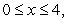 revolved about the line
revolved about the line 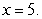 Draw a typical shell and write an integral that can be used to compute the volume of the solid.
Draw a typical shell and write an integral that can be used to compute the volume of the solid.
(Essay)
4.9/5  (39)
(39)
Find the area between the following curves on the given interval. 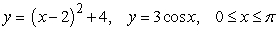
(Multiple Choice)
4.8/5  (42)
(42)
An object is dropped from a height of 100 feet. Another object directly below the first is launched vertically from the ground with an initial velocity of 50 ft/s. Determine when and how high up the objects collide.
(Essay)
4.7/5  (41)
(41)
Identify the integral used to determine the surface area of the surface of revolution for the shape described by 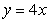 ,
, 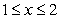 , revolved about the x-axis.
, revolved about the x-axis.
(Multiple Choice)
4.8/5  (36)
(36)
Starting with the expression for work  , one can change the look of the expression without changing what it represents by dividing the force F by the area it is applied over and multiplying the differential distance dx by that same area. Force divided by area is a pressure (P), and area times the differential distance is a differential volume. Hence one can also describe work as
, one can change the look of the expression without changing what it represents by dividing the force F by the area it is applied over and multiplying the differential distance dx by that same area. Force divided by area is a pressure (P), and area times the differential distance is a differential volume. Hence one can also describe work as 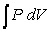 . A gas at constant temperature will change its pressure inversely to changes in volume,
. A gas at constant temperature will change its pressure inversely to changes in volume, 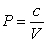 . If a sample of gas has a pressure of 1 atmosphere when its volume is 1 L, how much work does it do when it expands from 1 L to 4 L?
. If a sample of gas has a pressure of 1 atmosphere when its volume is 1 L, how much work does it do when it expands from 1 L to 4 L?
(Multiple Choice)
4.9/5  (38)
(38)
A given sample of a particular polymer will have molecules with a range of molecular weights, MW. If the molecular weight pdf is 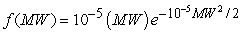 , what fraction of the molecules will have a molecular weight between 50 and 100?
, what fraction of the molecules will have a molecular weight between 50 and 100?
(Multiple Choice)
4.8/5  (40)
(40)
The base of a solid V is the region bounded by 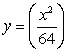 and
and 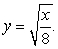 Find the volume if V has square cross sections.
Find the volume if V has square cross sections.
(Multiple Choice)
4.9/5  (42)
(42)
Is the function 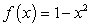 a probability density function on the interval
a probability density function on the interval 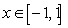 ?
?
(Multiple Choice)
4.8/5  (33)
(33)
Showing 1 - 20 of 113
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)