Exam 8: First-Order Differential Equations
Exam 1: Preliminaries143 Questions
Exam 2: Limits and Continuity125 Questions
Exam 3: Differentiation150 Questions
Exam 4: Applications of the Derivative143 Questions
Exam 5: Integration154 Questions
Exam 6: Applications of the Definite Integral113 Questions
Exam 7: Integration Techniques95 Questions
Exam 8: First-Order Differential Equations72 Questions
Exam 9: Infinite Series111 Questions
Exam 10: Parametric Equations and Polar Coordinates129 Questions
Exam 11: Vectors and the Geometry of Space107 Questions
Exam 12: Vector-Valued Functions103 Questions
Exam 13: Functions of Several Variables and Partial Differentiation112 Questions
Exam 14: Multiple Integrals92 Questions
Exam 15: Vector Calculus67 Questions
Exam 16: Second Order Differential Equations38 Questions
Select questions type
Is the following differential equation separable or not? 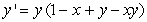
Free
(Multiple Choice)
4.7/5  (35)
(35)
Correct Answer:
A
Suppose the income tax structure is as follows: the first $28,000 is taxed at 20%, the remainder is taxed at 30%. Compute the tax 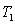 on an income of $40,000. Now suppose that inflation is 5% and you receive a cost of living (5%) raise to $42,000. Compute the tax
on an income of $40,000. Now suppose that inflation is 5% and you receive a cost of living (5%) raise to $42,000. Compute the tax  on this income. To compare the taxes you should adjust the tax
on this income. To compare the taxes you should adjust the tax  for inflation (add 5%).
for inflation (add 5%).
Free
(Essay)
4.9/5  (46)
(46)
Correct Answer:
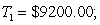
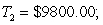 adjusted
adjusted 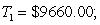
Write the following second-order equation as a system of first-order equations. 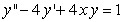
Free
(Essay)
4.7/5  (42)
(42)
Correct Answer:
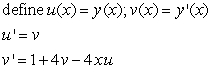
Find the solution to the following separable differential equation. 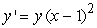
(Multiple Choice)
4.8/5  (33)
(33)
Use Euler's method with h = 0.1 to approximate y(1.0) and y(2.0) for the differential equation 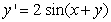 ,
, 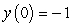 .
.
(Multiple Choice)
4.8/5  (34)
(34)
The University of XYZ has a goal to increase its endowment from the initial value of $100,000,000, to $150,000,000 over 4 years. If the interest rate earned by the endowment (after expenses) is 5% each year (compounded continuously), and the contributions become available continuously and at a constant rate, how much will they actually have to collect from contributors over those 4 years to meet their goal?
(Multiple Choice)
4.8/5  (39)
(39)
Consider a chemical system containing species A, B, and C; and that A and B can react to make C in a bimolecular reaction with rate constant of k1, and C can decompose to make A and B in a first order reaction with rate constant of k-1. If the instantaneous amounts of A, B, and C are represented as a, b, and c, and the initial amounts are given as A0, B0, and C0, the change in C can be represented with the differential equation ![Consider a chemical system containing species A, B, and C; and that A and B can react to make C in a bimolecular reaction with rate constant of k<sub>1</sub>, and C can decompose to make A and B in a first order reaction with rate constant of k<sub>-1</sub>. If the instantaneous amounts of A, B, and C are represented as a, b, and c, and the initial amounts are given as A<sub>0</sub>, B<sub>0</sub>, and C<sub>0</sub>, the change in C can be represented with the differential equation . If A<sub>0</sub> = 2 , B<sub>0</sub> = 2, C<sub>0</sub> = 0, k<sub>1</sub> = 0.04, and k<sub>-1</sub> = 0.04, solve the differential equation for c and graph the solution. [Note: c can never be larger than C<sub>0</sub> plus the smaller of A<sub>0</sub> or B<sub>0</sub>. Nor can it be smaller than 0.]](https://storage.examlex.com/TB2342/11eaa948_cce7_2035_84bc_9b5b210a4914_TB2342_11.jpg) . If A0 = 2 , B0 = 2, C0 = 0, k1 = 0.04, and k-1 = 0.04, solve the differential equation for c and graph the solution. [Note: c can never be larger than C0 plus the smaller of A0 or B0. Nor can it be smaller than 0.]
. If A0 = 2 , B0 = 2, C0 = 0, k1 = 0.04, and k-1 = 0.04, solve the differential equation for c and graph the solution. [Note: c can never be larger than C0 plus the smaller of A0 or B0. Nor can it be smaller than 0.]
(Essay)
4.8/5  (43)
(43)
Find all equilibrium points for the following system of equations. 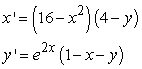
(Multiple Choice)
4.8/5  (36)
(36)
Identify the equilibrium solutions for 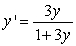 , and determine if they are stable or unstable.
, and determine if they are stable or unstable.
(Multiple Choice)
4.9/5  (38)
(38)
Identify the equilibrium solutions for 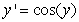 , for
, for 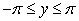 , and determine if they are stable or unstable.
, and determine if they are stable or unstable.
(Multiple Choice)
4.9/5  (36)
(36)
A stirred tank with volume, V, has a feed stream of concentrated floor cleaner flowing into it at a rate of f . The flow stream has a concentration of ci. The outlet stream also flows at f but with a concentration of c, the concentration of the floor cleaner solution in the tank. The rate of change of the concentration is proportional to the difference between ci and c with proportionality constant of f/V: 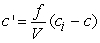 . If the tank volume is 2000 L, the flow rate is 6 L/min, the inlet concentration is 0.9, and the initial concentration of the floor cleaner in the tank is 0.0, how long until the concentration in the tank is 0.7?
. If the tank volume is 2000 L, the flow rate is 6 L/min, the inlet concentration is 0.9, and the initial concentration of the floor cleaner in the tank is 0.0, how long until the concentration in the tank is 0.7?
(Multiple Choice)
4.8/5  (37)
(37)
Find the solution of the differential equation, y' = -2y, satisfying the initial condition, y(3) = 0.
(Multiple Choice)
4.9/5  (40)
(40)
Solve the following initial value problem explicitly. 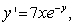 y(1) = -3
y(1) = -3
(Multiple Choice)
4.9/5  (39)
(39)
Use the direction field below to sketch a solution curve and estimate the initial value y(0) for the differential equation 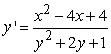 , such that the solution curve passes through the point (2, 2).
, such that the solution curve passes through the point (2, 2). 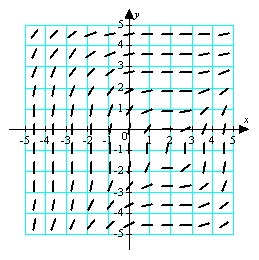
(Essay)
4.9/5  (49)
(49)
Match the appropriate slope field with the differential equation 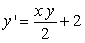 .
.
(Multiple Choice)
4.9/5  (39)
(39)
The rate at which water flows out of a drain in the bottom of a certain tank is proportional to the height of water in the tank. The tank is a vertical cylinder with cross-sectional area of 1.0 m2, so that every 1 cm in height represents 10 L. If the flow is 10 L/min (i.e. 1 cm/min) when the water level is 700 cm, how long will it take for the level to go from 700 cm to 30 cm?
(Multiple Choice)
4.9/5  (34)
(34)
The text describes logistic growth with an equation for the actual population in terms of a growth constant and a maximum population (carrying capacity), 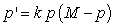 . The equation could also be written for a fraction of the maximum population in terms of a fractional growth constant. Re-express the differential equation in terms of the fractional population,
. The equation could also be written for a fraction of the maximum population in terms of a fractional growth constant. Re-express the differential equation in terms of the fractional population, 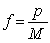 . Compare the time it takes for the population to go from 60% of the maximum to 80% of the maximum with the time it takes to go from 80% of the maximum to 90% of the maximum,
if k = 0.00100 day-1 and M = 4000?
. Compare the time it takes for the population to go from 60% of the maximum to 80% of the maximum with the time it takes to go from 80% of the maximum to 90% of the maximum,
if k = 0.00100 day-1 and M = 4000?
(Essay)
4.8/5  (48)
(48)
Showing 1 - 20 of 72
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)