Exam 11: Comparisons Involving Proportions and a Test of Independence

City planners are evaluating three proposed alternatives for relieving the growing traffic congestion on a north-south highway in a booming city. The proposed alternatives are: (1) designate high-occupancy vehicle (HOV) lanes on the existing highway, (2) construct a new, parallel highway, and (3) construct a light (passenger) rail system. In an analysis of the three proposals, a citizen group has raised the question of whether preferences for the three alternatives differ among residents near the highway and non-residents. A test of independence will address this question, with the hypotheses being: H₀: Proposal preference is independent of the residency status of the individual H_a: Proposal preference is not independent of the residency status of the individual A simple random sample of 500 individuals has been selected. The crosstabulation of the residency statuses and proposal preferences of the individuals sampled is shown below. 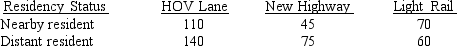Conduct a test of independence using  = .05 to address the question of whether residency status is independent of the proposal preference.

The degrees of freedom for a contingency table with 10 rows and 11 columns is

Of 150 Chattanooga residents surveyed, 60 indicated that they participated in a recycling program. In Knoxville, 120 residents were surveyed and 36 claimed to recycle. a.Determine a 95% confidence interval estimate for the difference between the proportions of residents recycling in the two cities. b.From your answer in Part a, is there sufficient evidence to conclude that there is a significant difference in the proportion of residents participating in a recycling program?

The results of a recent poll on the preference of voters regarding the presidential candidates are shown below. 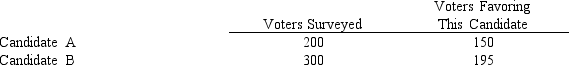a.Develop a 90% confidence interval estimate for the difference between the proportions of voters favoring each candidate. b.Does your confidence interval provide conclusive evidence that one of the candidates is favored more? Explain.

Exhibit 11-8 The table below gives beverage preferences for random samples of teens and adults. 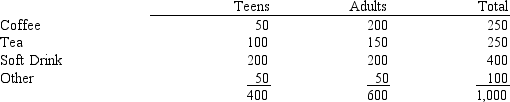We are asked to test for independence between age (i.e., adult and teen) and drink preferences. -Refer to Exhibit 11-8. The expected number of adults who prefer coffee is

Before the start of the Winter Olympics, it was expected that the percentages of medals awarded to the top contenders to be as follows. 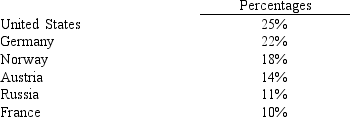Midway through the Olympics, of the 120 medals awarded, the following distribution was observed. We want to test to see if there is a significant difference between the expected and actual awards given. a.Compute the test statistic. b.Using the p-value approach, test to see if there is a significant difference between the expected and the actual values. Let   .05. c.At 95% confidence, test for a significant difference using the critical value approach.

Exhibit 11-1 The results of a recent poll on the preference of shoppers regarding two products are shown below. -Refer to Exhibit 11-1. The 95% confidence interval estimate for the difference between the populations favoring the products is

The degrees of freedom for a contingency table with 6 rows and 3 columns is

During the recent primary elections, the democratic presidential candidate showed the following pre-election voter support in Alabama and Mississippi. 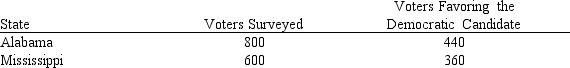a.We want to determine whether or not the proportions of voters favoring the Democratic candidate were the same in both states. Provide the hypotheses. b.Compute the test statistic. c.Determine the p-value; and at 95% confidence, test the above hypotheses.

Exhibit 11-7 In the past, 35% of the students at ABC University were in the Business College, 35% of the students were in the Liberal Arts College, and 30% of the students were in the Education College. To see whether or not the proportions have changed, a sample of 300 students was taken. Ninety of the sample students are in the Business College, 120 are in the Liberal Arts College, and 90 are in the Education College. -Refer to Exhibit 11-7. The calculated value for the test statistic equals

Exhibit 11-6 In order to determine whether or not a particular medication was effective in curing the common cold, one group of patients was given the medication, while another group received sugar pills. The results of the study are shown below. 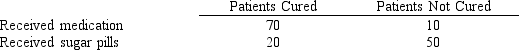We are interested in determining whether or not the medication was effective in curing the common cold. -Refer to Exhibit 11-6. The test statistic is

The results of a recent poll on the preference of voters regarding presidential candidates are shown below. At 95% confidence, test to determine whether or not there is a significant difference between the preferences for the two candidates.

Exhibit 11-4 When individuals in a sample of 150 were asked whether or not they supported capital punishment, the following information was obtained. We are interested in determining whether or not the opinions of the individuals (as to Yes, No, and No Opinion) are uniformly distributed. -Refer to Exhibit 11-4. The expected frequency for each group is

Exhibit 11-1 The results of a recent poll on the preference of shoppers regarding two products are shown below. -Refer to Exhibit 11-1. At 95% confidence, the margin of error is

A sample of 150 individuals (males and females) was surveyed, and the individuals were asked to indicate their yearly incomes. Their incomes were categorized as follows. 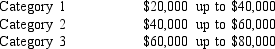The results of the survey are shown below. We want to determine if yearly income is independent of gender. a.Compute the test statistic. b.Using the p-value approach, test to determine if yearly income is independent of gender.

Exhibit 11-7 In the past, 35% of the students at ABC University were in the Business College, 35% of the students were in the Liberal Arts College, and 30% of the students were in the Education College. To see whether or not the proportions have changed, a sample of 300 students was taken. Ninety of the sample students are in the Business College, 120 are in the Liberal Arts College, and 90 are in the Education College. -Refer to Exhibit 11-7. The p-value is

A major automobile manufacturer claimed that the frequencies of repairs on all five models of its cars are the same. A sample of 200 repair services showed the following frequencies on the various makes of cars. At   0.05, test the manufacturer's claim.

The data below represents the fields of specialization for a randomly selected sample of undergraduate students. We want to determine whether there is a significant difference in the fields of specialization between regions of the country. 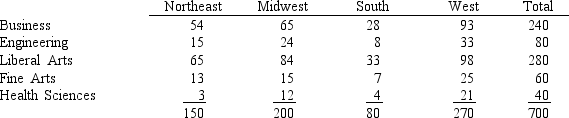a.Determine the critical value of the chi-square (x²) for this test of independence. b.Calculate the value of the test statistic. c.What is the conclusion for this test? Let   .05.

Assume we are interested in determining whether the proportion of voters planning to vote for candidate C (p_C) is significantly less than the proportion of voters planning to vote for candidate B (p_B). The correct null hypothesis for testing the above is

Both the hypothesis test for proportions of a multinomial population and the test of independence focus on the difference between