Question 1

If X and Y are mutually exclusive events with P(X) F1F1F1S1F1F1F10 0.295, P(Y) F1F1F1S1F1F1F10 0.32, then P(XF1F1F1S1F1F1F10Y) F1F1F1S1F1F1F10

Accepted Answer

A) 0.0944 
B) 0.6150 
C) 1.0000 
D) 0.0000 
A) 0.0944 
B) 0.6150 
C) 1.0000 
D) 0.0000 D

Question 2

The probability of the intersection of two mutually exclusive events

Accepted Answer

A) can be any value between 0 to 1 
B) must always be equal to 1 
C) must always be equal to 0 
D) can be any positive value 
A) can be any value between 0 to 1 
B) must always be equal to 1 
C) must always be equal to 0 
D) can be any positive value C

Question 3

The union of events A and B is the event containing

Accepted Answer

A) all the sample points common to both A and B 
B) all the sample points belonging to A or B 
C) all the sample points belonging to A or B or both 
D) all the sample points belonging to A or B, but not both 
A) all the sample points common to both A and B 
B) all the sample points belonging to A or B 
C) all the sample points belonging to A or B or both 
D) all the sample points belonging to A or B, but not both C

Question 4

It is estimated that 3% of the athletes competing in a large tournament are users of an illegal drug to enhance performance. The test for this drug is 90% accurate. What is the probability that an athlete who tests positive is actually a user?

Accepted Answer

The answer of It is estimated that 3% of the...

Question 5

In a city, 60% of the residents live in houses and 40% of the residents live in apartments. Of the people who live in houses, 20% own their own business. Of the people who live in apartments, 10% own their own business. If a person owns his or her own business, find the probability that he or she lives in a house.

Accepted Answer

The answer of In a city, 60% of the residents...

Question 6

In the two upcoming basketball games, the probability that UTC will defeat Marshall is 0.63, and the probability that UTC will defeat Furman is 0.55. The probability that UTC will defeat both opponents is 0.3465.
a.What is the probability that UTC will defeat Furman given that they defeat Marshall?
b.What is the probability that UTC will win at least one of the games?
c.What is the probability of UTC winning both games?
d.Are the outcomes of the games independent? Explain and substantiate your answer.

Accepted Answer

a.0.55
b.0.8335
c.0.3465
d.Yes

Question 7

Bayes' theorem is used to compute

Accepted Answer

A) the prior probabilities 
B) the union of events 
C) both the prior probabilities and the union of events 
D) the posterior probabilities 
A) the prior probabilities 
B) the union of events 
C) both the prior probabilities and the union of events 
D) the posterior probabilities

Question 8

The set of all possible sample points (experimental outcomes) is called

Accepted Answer

A) a sample 
B) an event 
C) the sample space 
D) a population 
A) a sample 
B) an event 
C) the sample space 
D) a population

Question 9

Two events, A and B, are mutually exclusive and each has a nonzero probability. If event A is known to occur, the probability of the occurrence of event B is

Accepted Answer

A) one 
B) any positive value 
C) zero 
D) any value between 0 to 1 
A) one 
B) any positive value 
C) zero 
D) any value between 0 to 1

Question 10

If P(A|B) = .3 and P(B) = .8, then

Accepted Answer

A) P(
A)  = .24 
B) P(B|
A)  = .7 
C) P(A F1F1F1S1F1F1F10 
B)  = .5 
D) P(A F1F1F1S1F1F1F10 
B)  = .24 
A) P(
A)  = .24 
B) P(B|
A)  = .7 
C) P(A F1F1F1S1F1F1F10 
B)  = .5 
D) P(A F1F1F1S1F1F1F10 
B)  = .24

Question 11

A perfectly balanced coin is tossed 6 times and tails appears on all six tosses. Then, on the seventh trial

Accepted Answer

A) tails cannot appear 
B) heads has a larger chance of appearing than tails 
C) tails has a better chance of appearing than heads 
D) None of the other answers is correct. 
A) tails cannot appear 
B) heads has a larger chance of appearing than tails 
C) tails has a better chance of appearing than heads 
D) None of the other answers is correct.

Question 12

All the employees of ABC Company are assigned ID numbers. The ID number consists of the first letter of an employee's last name, followed by four numbers.
a.How many possible different ID numbers are there?
b.How many possible different ID numbers are there for employees whose last name starts with an "A"?

Accepted Answer

The answer of All the employees of ABC Company are...

Question 13

If A and B are independent events with P(A) F1F1F1S1F1F1F10 0.4 and P(B) F1F1F1S1F1F1F10 0.6, then P(A F1F1F1S1F1F1F10 B) F1F1F1S1F1F1F10

Accepted Answer

A) 0.76 
B) 1.00 
C) 0.24 
D) 0.2 
A) 0.76 
B) 1.00 
C) 0.24 
D) 0.2

Question 14

If a penny is tossed three times and comes up heads all three times, the probability of heads on the fourth trial is

Accepted Answer

A) smaller than the probability of tails 
B) larger than the probability of tails 
C) 1/16 
D) None of the other answers is correct. 
A) smaller than the probability of tails 
B) larger than the probability of tails 
C) 1/16 
D) None of the other answers is correct.

Question 15

Initial estimates of the probabilities of events are known as

Accepted Answer

A) sets 
B) posterior probabilities 
C) conditional probabilities 
D) prior probabilities 
A) sets 
B) posterior probabilities 
C) conditional probabilities 
D) prior probabilities

Question 16

There are two more assignments in a class before its end, and if you get an A on at least one of them, you will get an A for the semester. Your subjective assessment of your performance is
   
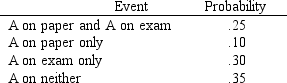a. What is the probability of getting an A on the paper?
b. What is the probability of getting an A on the exam?
c. What is the probability of getting an A in the course?
d. Are the grades on the assignments independent?

Accepted Answer

a. .35
b.

Question 17

A survey of business students who had taken the Graduate Management Admission Test (GMAT) indicated that students who have spent at least five hours studying GMAT review guides have a probability of 0.85 of scoring above 400. Students who do not spend at least five hours reviewing have a probability of 0.65 of scoring above 400. It has been determined that 70% of the business students spent at least five hours reviewing for the test.
a.Find the probability of scoring above 400.
b.Find the probability that given a student scored above 400, he/she spent at least five hours reviewing for the test.

Accepted Answer

The answer of A survey of business students who had...

Question 18

Three applications for admission to a local university are checked to determine whether each applicant is male or female. The number of sample points in this experiment is

Accepted Answer

A) 2 
B) 4 
C) 6 
D) 8 
A) 2 
B) 4 
C) 6 
D) 8

Question 19

In a recent survey in a Statistics class, it was determined that only 60% of the students attend class on Fridays. From past data it was noted that 98% of those who went to class on Fridays pass the course, while only 20% of those who did not go to class on Fridays passed the course.
a.What percentage of students is expected to pass the course?
b.Given that a person passes the course, what is the probability that he/she attended classes on Fridays?

Accepted Answer

The answer of In a recent survey in a Statistics...

Question 20

As a company manager for Claimstat Corporation there is a 0.40 probability that you will be promoted this year. There is a 0.72 probability that you will get a promotion or a raise. The probability of getting a promotion and a raise is 0.25.
a.If you get a promotion, what is the probability that you will also get a raise?
b.What is the probability of getting a raise?
c.Are getting a raise and being promoted independent events? Explain using probabilities.
d.Are these two events mutually exclusive? Explain using probabilities.

Accepted Answer

a.0.625
b.0.57
c.No, because P

If X and Y are mutually exclusive events with P(X)  0.295, P(Y)  0.32, then P(XY) 

The probability of the intersection of two mutually exclusive events

The union of events A and B is the event containing

It is estimated that 3% of the athletes competing in a large tournament are users of an illegal drug to enhance performance. The test for this drug is 90% accurate. What is the probability that an athlete who tests positive is actually a user?

Bayes' theorem is used to compute

The set of all possible sample points (experimental outcomes) is called

Two events, A and B, are mutually exclusive and each has a nonzero probability. If event A is known to occur, the probability of the occurrence of event B is

If P(A|B) = .3 and P(B) = .8, then

A perfectly balanced coin is tossed 6 times and tails appears on all six tosses. Then, on the seventh trial

If A and B are independent events with P(A)  0.4 and P(B)  0.6, then P(A  B) 

If a penny is tossed three times and comes up heads all three times, the probability of heads on the fourth trial is

Initial estimates of the probabilities of events are known as

Three applications for admission to a local university are checked to determine whether each applicant is male or female. The number of sample points in this experiment is

Data and Statistics

Descriptive Statistics: Tabular and Graphical Presentations

Descriptive Statistics: Numerical Measures

Discrete Probability Distributions

Continuous Probability Distributions

Sampling and Sampling Distributions

Interval Estimation

Hypothesis Tests

Comparisons Involving Means, Experimental Design, and Analysis of Variance

Comparisons Involving Proportions and a Test of Independence

Simple Linear Regression

Multiple Regression

Statistical Methods for Quality Control

Time Series Analysis and Forecastng

Filters

Exam 4: Introduction to Probability

If X and Y are mutually exclusive events with P(X)  0.295, P(Y)  0.32, then P(XY) 

The probability of the intersection of two mutually exclusive events

The union of events A and B is the event containing

It is estimated that 3% of the athletes competing in a large tournament are users of an illegal drug to enhance performance. The test for this drug is 90% accurate. What is the probability that an athlete who tests positive is actually a user?

Bayes' theorem is used to compute

The set of all possible sample points (experimental outcomes) is called

Two events, A and B, are mutually exclusive and each has a nonzero probability. If event A is known to occur, the probability of the occurrence of event B is

If P(A|B) = .3 and P(B) = .8, then

A perfectly balanced coin is tossed 6 times and tails appears on all six tosses. Then, on the seventh trial

If A and B are independent events with P(A)  0.4 and P(B)  0.6, then P(A  B) 

If a penny is tossed three times and comes up heads all three times, the probability of heads on the fourth trial is

Initial estimates of the probabilities of events are known as

Three applications for admission to a local university are checked to determine whether each applicant is male or female. The number of sample points in this experiment is

Data and Statistics

Descriptive Statistics: Tabular and Graphical Presentations

Descriptive Statistics: Numerical Measures

Discrete Probability Distributions

Continuous Probability Distributions

Sampling and Sampling Distributions

Interval Estimation

Hypothesis Tests

Comparisons Involving Means, Experimental Design, and Analysis of Variance

Comparisons Involving Proportions and a Test of Independence

Simple Linear Regression

Multiple Regression

Statistical Methods for Quality Control

Time Series Analysis and Forecastng

Filters