Exam 9: Hypothesis Tests

Several years ago the proportion of Americans aged 18 - 24 who invested in the stock market was 0.20. A random sample of 25 Americans in this age group was recently taken. They were asked whether or not they invested in the stock market. The results follow: 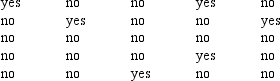At a .05 level of significance, use Excel to determine whether or not the proportion of Americans 18 - 24 years old that invest in the stock market has changed.

For a two-tailed hypothesis test about , we can use any of the following approaches except

Fast 'n Clean operates 12 laundromats on the east side of the city. All of Fast 'n Clean's clothes dryers have a label stating "20 minutes for $1.00." You question the accuracy of the dryers' clocks and decide to conduct an observational study. You randomly select 36 dryers in several different Fast 'n Clean locations, put $1.00 in each and time the drying cycle. The sample mean drying time is 20 minutes and 25 seconds. The manufacturer of the dryer states that the standard deviation for 20-minute drying cycles is 1 minute. a. Using the sample data and  = .05, test the validity of the label on the dryers. Apply the p-value and critical value approaches to conducting the two-tail hypothesis test. b. Conduct the same two-tail hypothesis test, but this time use the confidence interval approach to hypothesis testing.

In a television commercial, the manufacturer of a toothpaste claims that at least 4 out of 5 dentists recommend its product. A consumer-protection group wants to test that claim. Identify the hypotheses.

A meteorologist stated that the average temperature during July in Chattanooga was 80 degrees. A sample of 32 Julys was taken. The correct set of hypotheses is

A student believes that the average grade on the statistics final examination is 87. A sample of 36 final examinations is taken. The average grade in the sample is 83.96. The population variance is 144. a.State the null and alternative hypotheses. b.Using a critical value, test the hypothesis at the 5% level of significance. c.Using a p-value, test the hypothesis at the 5% level of significance. d.Using a confidence interval, test the hypothesis at the 5% level of significance. e.Compute the probability of a Type II error if the average grade on the final is 85.

A fast food restaurant is considering a promotion that will offer customers to purchase a toy featuring a cartoon movie character. If more than 20% of the customers purchase the toy, the promotion will be profitable. A sample of 50 restaurants is used to test the promotion. a.State the hypotheses associated with the restaurant's test. b.Describe a Type I error for this situation. c.Describe a Type II error for this situation.

Exhibit 9-1 -Refer to Exhibit 9-1. If the test is done at a .05 level of significance, the null hypothesis should

You are given the following information obtained from a random sample of 5 observations. 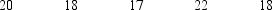At a 10% level of significance, use Excel to determine whether or not the mean of the population from which this sample was taken is significantly less than 21. (Assume the population is normally distributed.)

The board of directors of a corporation has agreed to allow the human resources manager to move to the next step in planning day care service for employees' children if the manager can prove that at least 25% of the employees have interest in using the service. The HR manager polls 300 employees and 90 say they would seriously consider utilizing the service. At the  = .10 level of significance, is there enough interest in the service to move to the next planning step?

Exhibit 9-5 Assume population is normally distributed. -Refer to Exhibit 9-5. The test statistic equals

Exhibit 9-1 -Refer to Exhibit 9-1. The test statistic equals

An official of a large national union claims that the fraction of women in the union is not significantly different from one-half. Using the sample information reported below, carry out a test of this statement. Use a .05 level of significance.

For a two-tailed test with a sample size of 40, the null hypothesis will not be rejected at a 5% level of significance if the test statistic is

In the past the average age of employees of a large corporation has been 40 years. Recently, the company has been hiring older individuals. In order to determine whether there has been an increase in the average age of all the employees, a sample of 25 employees was selected. The average age in the sample was 45 years with a standard deviation of 5 years. Assume the distribution of the population is normal. Let   .05. a.State the null and the alternative hypotheses. b.Test to determine whether or not the mean age of all employees is significantly more than 40 years.

A sample of 81 account balances of a credit company showed an average balance of $1,200. The population standard deviation is $126. You want to determine if the mean of all account balances is significantly different from $1,150. Use a .05 level of significance.

Exhibit 9-3 -Refer to Exhibit 9-3. If the test is done at a 5% level of significance, the null hypothesis should

A national poll reported that 58% of those with Internet access have made purchases online. To investigate whether this percentage applies to its own state, a legislator commissions a study. A random sample of 400 state residents who have Internet access is taken. Of those 400 respondents, 215 said that they have made purchases online. Does this sample provide sufficient evidence to conclude that the state differs from the nation with respect to making purchases online? Use the p-value to conduct the hypothesis test and use a .05 level of significance.

A lathe is set to cut bars of steel into lengths of 6 centimeters. The lathe is considered to be in perfect adjustment if the average length of the bars it cuts is 6 centimeters. A sample of 121 bars is selected randomly and measured. It is determined that the average length of the bars in the sample is 6.08 centimeters. The population standard deviation is 0.44 centimeters. Determine whether or not the lathe is in perfect adjustment. Use a .05 level of significance.

Read the z statistic from the normal distribution table and circle the correct answer. A one-tailed test (lower tail) at a .063 level of significance; z 