Exam 5: Discrete Probability Distributions

A probability distribution showing the probability of x successes in n trials, where the probability of success does not change from trial to trial, is termed a

When using Excel's HYPGEOM.DIST function, one should choose TRUE for the fifth input if

A local university reports that 3% of their students take their general education courses on a pass/fail basis. Assume that fifty students are registered for a general education course. a.Define the random variable in words for this experiment. b.What is the expected number of students who have registered on a pass/fail basis? c.What is the probability that exactly five are registered on a pass/fail basis? d.What is the probability that more than three are registered on a pass/fail basis? e.What is the probability that less than four are registered on a pass/fail basis?

Which of the following properties of a binomial experiment is called the stationarity

When sampling without replacement, the probability of obtaining a certain sample is best given by a

John parks cars at a hotel. On the average, 6.7 cars will arrive in an hour. Assume that a driver's decision on whether to let John park the car does not depend upon any other person's decision. Define the random variable x to be the number of cars arriving in any hour period. a.What is the appropriate probability distribution for x? Explain how x satisfies the properties of the distribution. b.Compute the probability that exactly 5 cars will arrive in the next hour. c.Compute the probability that no more than 5 cars will arrive in the next hour.

Compute the hypergeometric probabilities for the following values of n and x. Assume N  8 and r  5. a.n  5, x  2 b.n  6, x  4 c.n  3, x  0 d.n  3, x  3

A binomial probability distribution with p = .3 is

The number of customers that enter a store during one day is an example of

A production process produces 2% defective parts. A sample of 5 parts from the production is selected. What is the probability that the sample contains exactly two defective parts? Use the binomial probability function and show your computations to answer this question.

The expected value of a random variable is the

The probability distribution of the daily demand for a product is shown below. 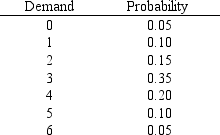a.What is the expected number of units demanded per day? b.Determine the variance and the standard deviation.

If one wanted to find the probability of ten customer arrivals in an hour at a service station, one would generally use the

The binomial probability distribution is used with

Ralph's Gas Station is running a giveaway promotion. With every fill-up of gasoline, Ralph gives out a lottery ticket that has a 25% chance of being a winning ticket. Customers who collect four winning lottery tickets are eligible for the "BIG SPIN" for large payoffs. What is the probability of qualifying for the big spin if a customer fills up: (a) 3 times; (b) 4 times; (c) 7 times?

A manufacturing company has 5 identical machines that produce nails. The probability that a machine will break down on any given day is 0.1. Define a random variable x to be the number of machines that will break down in a day. a.What is the appropriate probability distribution for x? Explain how x satisfies the properties of the distribution. b.Compute the probability that 4 machines will break down. c.Compute the probability that at least 4 machines will break down. d.What is the expected number of machines that will break down in a day? e.What is the variance of the number of machines that will break down in a day?

Assume that you have a binomial experiment with p  0.5 and a sample size of 100. The expected value of this distribution is

Exhibit 5-11 The random variable x is the number of occurrences of an event over an interval of ten minutes. It can be assumed that the probability of an occurrence is the same in any two time periods of an equal length. It is known that the mean number of occurrences in ten minutes is 5.3. -Refer to Exhibit 5-11. The probability that there are less than 3 occurrences is

Exhibit 5-9 Forty percent of all registered voters in a national election are female. A random sample of 5 voters is selected. -Refer to Exhibit 5-9. What is the random variable in this experiment?

The demand for a product varies from month to month. Based on the past year's data, the following probability distribution shows MNM company's monthly demand. a.Determine the expected number of units demanded per month. b.Each unit produced costs the company $8.00, and is sold for $10.00. How much will the company gain or lose in a month if they stock the expected number of units demanded, but sell 2000 units?