Exam 3: Linear Programming: Computer Solution and Sensitivity Analysis

Given the following linear programming problem that minimizes cost: Min Z = 2x + 8y Subject to (1) 8x + 4y ? 64       (2) 2x + 4y ? 32       (3) y ? 2 -At the optimal solution, the minimum cost is:

The shadow price for a positive decision variable is 0.

The sensitivity range for a(n) ________ coefficient is the range of values over which the current optimal solution point (product mix) will remain optimal.

The sensitivity range for a constraint quantity value is the range over which the shadow price is valid.

The sensitivity range for an objective function coefficient is the range of values over which the current optimal solution point (product mix) will remain optimal.

Aunt Anastasia operates a small business: she produces seasonal ceramic objects to sell to tourists. For the spring, she is planning to make baskets, eggs, and rabbits. Based on your discussion with your aunt you construct the following table: $\begin{array} { l c c c c } \text { Product } & \begin{array} { c } \text { Mix/mold } \\\text { requirements (lb) }\end{array} & \begin{array} { c } \text { Kiln } \\\text { (units) }\end{array} & \begin{array} { c } \text { Paint \& Seal } \\\text { (hr) }\end{array} & \begin{array} { c } \text { Profit/product } \\\text { (\$) }\end{array} \\\hline \text { Baskets } & 0.500 & 1 & 0.250 & \$ 2.50 \\\text { Eggs } & 0.333 & 1 & 0.333 & \$ 1.50 \\\text { Rabbits } & 0.250 & 1 & 0.750 & \$ 2.00 \\\text { Capacity } & 20 \text { pounds } & 50 \text { units } & 80 \text { hours } & \\\hline\end{array}$ Your aunt also has committed to make 25 rabbits for a charitable organization. Based on the information in the table, you formulate the problem as a linear program. B = number of baskets produced E = number of eggs produced R = number of rabbits produced MAX 2.5B + 1.5E + 2R s.t. 0.5B + 0.333E + 0.25R ≤ 20 B + E + R ≤ 50 0.25B + 0.333E + 0.75R ≤ 80 R ≥ 25 The Excel solution and the answer and sensitivity report are shown below. The Answer Report: Target Cell (Max) Cell Name Original Value Final Value \ C\ 21 Profit 0 \ 112.5 $\text { Adjustable Cells }$ Cell Name Original Value Final Value \ C\ 18 Baskets 0 25 \ C\ 19 Eggs 0 0 \ C\ 20 Rabbits 0 25 $\text { Constraints }$ Cell Name Cell Value Formula Status Slack Not \G \1 3 Mix/mold 18.75 \G \1 3<= \F \1 3 Binding 1.25 \G \1 4 Kiln 50 \G \1 4<= \F \1 4 Binding 0 Not \G \1 5 Paint and Seal 25 \G \1 5<= \F \1 5 Binding 55 \G \1 6 Demand 25 \G \1 6>= \F \1 6 Binding 0 The Sensitivity Report: $\text { Adjustable Cells }$ Cell Name Final Value Reduced Cost Objective Coefficient Allowable Increase Allowable Decrease \ C\ 18 Baskets 25 0 2.5 1+30 0.5 \C \1 9 Eggs 0 -1 1.5 1 1+30 \C \2 0 Rabbits 25 0 2 0.5 1+30 $\text { Constraints }$ Cell Name Final Value Shadow Price Constraint R.H. Side Allowable Increase Allowable Decrease \ G\ 13 Mix/mold 18.75 0 20 1+30 1.25 \ G\ 14 Kiln 50 2.5 50 2.5 25 \ G\ 15 Paint and Seal 25 0 80 1+30 55 \G \1 6 Demand 25 -0.5 25 25 5 -Aunt Anastasia feels that her prices are too low, particularly for her eggs. How much would her profit have to increase on the eggs before it is profitable for her to make and sell eggs?

Taco Loco is considering a new addition to their menu. They have test marketed a number of possibilities and narrowed them down to three new products, X, Y, and Z. Each of these products is made from a different combination of beef, beans, and cheese, and each product has a price point. Taco Loco feels they can sell an X for $17, a Y for $13, and a Z for $14. The company's management science consultant formulates the following linear programming model for company management. Max R = 14Z + 13Y + 17X subject to: Beef   2Z + 3Y + 4X ? 28 Cheese  9Z + 8Y + 11X ? 80 Beans  4Z + 4Y + 2X ? 68 X,Y,Z ? 0 The sensitivity report from the computer model reads as follows: $\text { Variable Cells }$ Cell Name Final Value Reduced Cost Objective Coefficient Allowable Increase Allowable Decrease \C \4 1.45 0 14 0.63 5.33 \D \4 Y 8.36 0 13 8 0.56 \E \4 0 -0.818 17 0.818 1+30 $\text { Constraints }$ Cell Name Final Value Shadow Price Constraint R.H. Side Allowable Increase Allowable Decrease \F \6 Beef 28 0.45 28 2 10.22 \F \7 Cheese 80 1.45 80 46 5.33 \FS 8 Beans 39.27 0 68 1+30 28.73 -The local cheese vendor offers to sell Taco Loco 200 pounds of cheese for these three products. Taco Loco should

Mallory Furniture buys two products for resale: big shelves (B) and medium shelves (M). Each big shelf costs $500 and requires 100 cubic feet of storage space, and each medium shelf costs $300 and requires 90 cubic feet of storage space. The company has $75,000 to invest in shelves this week, and the warehouse has 18,000 cubic feet available for storage. Profit for each big shelf is $300 and for each medium shelf is $150. Graphically solve this problem and answer the following questions. -Determine the sensitivity range for the profit on the big shelf.

The production manager for the Whoppy soft drink company is considering the production of two kinds of soft drinks: regular and diet. The company operates one 8-hour shift per day. Therefore, the production time is 480 minutes per day. During the production process, one of the main ingredients, syrup, is limited to maximum production capacity of 675 gallons per day. Production of a regular case requires 2 minutes and 5 gallons of syrup, while production of a diet case needs 4 minutes and 3 gallons of syrup. Profits for regular soft drink are $3.00 per case and profits for diet soft drink are $2.00 per case. -The sensitivity range for the profit on a regular case of soda is

Aunt Anastasia operates a small business: she produces seasonal ceramic objects to sell to tourists. For the spring, she is planning to make baskets, eggs, and rabbits. Based on your discussion with your aunt you construct the following table: $\begin{array} { l c c c c } \text { Product } & \begin{array} { c } \text { Mix/mold } \\\text { requirements (lb) }\end{array} & \begin{array} { c } \text { Kiln } \\\text { (units) }\end{array} & \begin{array} { c } \text { Paint \& Seal } \\\text { (hr) }\end{array} & \begin{array} { c } \text { Profit/product } \\\text { (\$) }\end{array} \\\hline \text { Baskets } & 0.500 & 1 & 0.250 & \$ 2.50 \\\text { Eggs } & 0.333 & 1 & 0.333 & \$ 1.50 \\\text { Rabbits } & 0.250 & 1 & 0.750 & \$ 2.00 \\\text { Capacity } & 20 \text { pounds } & 50 \text { units } & 80 \text { hours } & \\\hline\end{array}$ Your aunt also has committed to make 25 rabbits for a charitable organization. Based on the information in the table, you formulate the problem as a linear program. B = number of baskets produced E = number of eggs produced R = number of rabbits produced MAX 2.5B + 1.5E + 2R s.t.    0.5B + 0.333E + 0.25R ? 20    B + E + R ? 50    0.25B + 0.333E + 0.75R ? 80    R ? 25 The Excel solution and the answer and sensitivity report are shown below. The Answer Report: Target Cell (Max) Cell Name Original Value Final Value \ C\ 21 Profit 0 \ 112.5 $\text { Adjustable Cells }$ Cell Name Original Value Final Value \ C\ 18 Baskets 0 25 \ C\ 19 Eggs 0 0 \ C\ 20 Rabbits 0 25 $\text { Constraints }$ Cell Name Cell Value Formula Status Slack Not \G \1 3 Mix/mold 18.75 \G \1 3<= \F \1 3 Binding 1.25 \G \1 4 Kiln 50 \G \1 4<= \F \1 4 Binding 0 Not \G \1 5 Paint and Seal 25 \G \1 5<= \F \1 5 Binding 55 \G \1 6 Demand 25 \G \1 6>= \F \1 6 Binding 0 The Sensitivity Report: $\text { Adjustable Cells }$ Cell Name Final Value Reduced Cost Objective Coefficient Allowable Increase Allowable Decrease \ C\ 18 Baskets 25 0 2.5 1+30 0.5 \C \1 9 Eggs 0 -1 1.5 1 1+30 \C \2 0 Rabbits 25 0 2 0.5 1+30 $\text { Constraints }$ Cell Name Final Value Shadow Price Constraint R.H. Side Allowable Increase Allowable Decrease \ G\ 13 Mix/mold 18.75 0 20 1+30 1.25 \ G\ 14 Kiln 50 2.5 50 2.5 25 \ G\ 15 Paint and Seal 25 0 80 1+30 55 \G \1 6 Demand 25 -0.5 25 25 5 -Which additional resources would you recommend that Aunt Anastasia try to obtain?

Billy's Blues sells 3 types of T-shirts: Astro, Bling, and Curious. Manufacturing Astros requires 2 minutes of machine time and 20 minutes of labor, and costs $10. Brand Bling requires 2.5 minutes of machine time and 30 minutes of labor, and costs $14 to produce. Brand Curious requires 3 minutes of machine time and 45 minutes of labor, and costs $18 to produce. There are 300 machining hours available per week, 3750 labor hours, and he has a budget of $3000. Brand Astro sells for $15, Brand Bling for $18, and Brand Curious for $25. The LP formulation that maximizes week profit shown below. MAX 15A +18B + 25 C s.t.    2A + 2.5B + 3C ? 300    20A + 30B + 45C ? 3750    10A + 14B + 18C ? 3000 The solution from QM for Windows is show below. 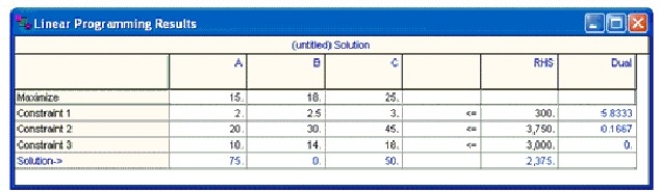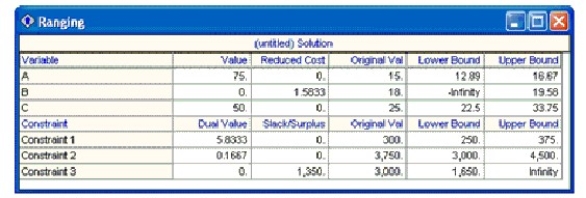-If one of Billy's machines breaks down, it usually results in about 6 hours of downtime. When this happens, Billy's profits are reduced by:

Most computer linear programming packages readily accept constraints entered in fractional form, such as X1/X3.

Use the constraints given below and determine which of the following points is feasible.    (1) 14x + 6y ? 42    (2) x - y ? 3

The simplex method is a graphical technique used to solve all management science problems.

Billy's Blues sells 3 types of T-shirts: Astro, Bling, and Curious. Manufacturing Astros requires 2 minutes of machine time and 20 minutes of labor, and costs $10. Brand Bling requires 2.5 minutes of machine time and 30 minutes of labor, and costs $14 to produce. Brand Curious requires 3 minutes of machine time and 45 minutes of labor, and costs $18 to produce. There are 300 machining hours available per week, 3750 labor hours, and he has a budget of $3000. Brand Astro sells for $15, Brand Bling for $18, and Brand Curious for $25. The LP formulation that maximizes week profit shown below. MAX 15A +18B + 25 C s.t. 2A + 2.5B + 3C ≤ 300 20A + 30B + 45C ≤ 3750 10A + 14B + 18C ≤ 3000 The solution from QM for Windows is show below. -Billy has decided that he can raise the price on the Curious t-shirt by 10% without losing sales. If he raises the price, his profits will

The sensitivity range for a ________ is the range of values over which the quantity values can change without changing the shadow price.

For a maximization problem, assume that a constraint is binding. If the original amount of a resource is 4 lbs. and the range of feasibility (sensitivity range) for this constraint is from 3 lbs. to 6 lbs., increasing the amount of this resource by 1 lb. will result in the

For a linear programming problem, assume that a given resource has not been fully used. We can conclude that the shadow price associated with that constraint

Tracksaws, Inc. makes tractors and lawn mowers. The firm makes a profit of $30 on each tractor and $30 on each lawn mower, and they sell all they can produce. The time requirements in the machine shop, fabrication, and tractor assembly are given in the table. Machine Shop Fabrication Assembly Tractor 2 hours 2 hours 1 hour Lawn Mower 1 hour 3 hours 0 hour Hrs. Available 60 hours 120 hours 45 hours Formulation: Let x = number of tractors produced per period y = number of lawn mowers produced per period MAX 30x+30y subject to 2x+y\leq60 2x+3y\leq120 x\leq45 The graphical solution is shown below. 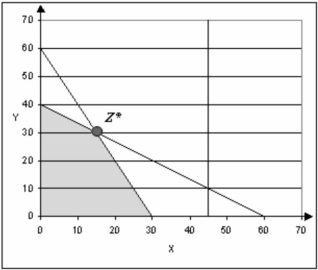-A breakdown in fabrication causes the available hours to drop from 120 to 90 hours. How will this impact the optimal number of tractors and mowers produced?

Consider the following linear program, which maximizes profit for two products--regular (R) and super (S): MAX 50R + 75S s.t.    1.2 R + 1.6 S ? 600 assembly (hours)    0.8 R + 0.5 S ? 300 paint (hours) .   16 R + 0.4 S ? 100 inspection (hours) Sensitivity Report: Cell Name Final Value Reduced Cost Objective Coefficient Allowable Increase Allowable Decrease \ \ 7 Regular = 291.67 0.00 50 70 20 \C \ 7 Super = 133.33 0.00 75 50 43.75 Cell Name Final Value Shadow Price Constraint R.H. Side Allowable Increase Allowable Decrease \ \ 3 Assembly (hr/unit) 563.33 0.0 600 1 mathrm E +30 36.67 mathrm E \ 4 Paint (hr/unit) 300.00 33.33 300 39.29 175 mathrm E \ 5 Inspect (hr/unit) 100.00 145.83 100 12.94 40 -If the company wanted to increase the available hours for one of their constraints (assembly, painting, or inspection) by two hours, they should increase ________.