Exam 3: Linear Programming: Computer Solution and Sensitivity Analysis

Given the following linear programming problem that minimizes cost: Min Z = 2x + 8y Subject to (1) 8x + 4y ? 64       (2) 2x + 4y ? 32       (3) y ? 2 -What is the sensitivity range for the cost of x?

The terms shadow price and dual price mean the same thing.

Tracksaws, Inc. makes tractors and lawn mowers. The firm makes a profit of $30 on each tractor and $30 on each lawn mower, and they sell all they can produce. The time requirements in the machine shop, fabrication, and tractor assembly are given in the table. Machine Shop Fabrication Assembly Tractor 2 hours 2 hours 1 hour Lawn Mower 1 hour 3 hours 0 hour Hrs. Available 60 hours 120 hours 45 hours Formulation: Let x = number of tractors produced per period y = number of lawn mowers produced per period Let x = number of tractors produced per period y = number of lawn mowers produced per period MAX 30x + 30y subject to  2x + y ? 60     2x + 3y ? 120     x ? 45 The graphical solution is shown below. 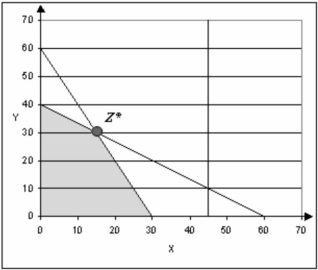-Determine the sensitivity range for the profit for tractors.

The linear programming problem whose output follows is used to determine how many bottles of red nail polish (x1), blue nail polish (x2), green nail polish (x3), and pink nail polish (x4) a beauty salon should stock. The objective function measures profit; it is assumed that every piece stocked will be sold. Constraint 1 measures display space in units, constraint 2 measures time to set up the display in minutes. Note that green nail polish does not require any time to prepare its display. Constraints 3 and 4 are marketing restrictions. Constraint 3 indicates that the maximum demand for red and green polish is 25 bottles, while constraint 4 specifies that the minimum demand for blue, green, and pink nail polish bottles combined is at least 50 bottles. MAX $100 x _ { 1 } + 120 x _ { 2 } + 150 x _ { 3 } + 125 x _ { 4 }$ Subject to 1 . $x _ { 1 } + 2 x _ { 2 } + 2 x _ { 3 } + 2 x _ { 4 } \leq 108$    2. $3 x _ { 1 } + 5 x _ { 2 } + x _ { 4 } \leq 120$    3. $x _ { 1 } + x _ { 3 } \leq 25$    4. $x _ { 2 } + x _ { 3 } + x _ { 4 } \geq 50$     $x _ { 1 } , x _ { 2 } , x _ { 3 } , x _ { 4 } \geq 0$ Optimal Solution: Objective Function Value = 7475.000 Variable Value Reduced Costs 8 0 0 5 17 0 33 0 Constraint Slack/ Surplus Dual Prices 1 0 75 2 63 0 3 0 25 4 0 -25 Objective Coefficient Ranges Variable Lower Limit Current Value Upper Limit 87.5 100 none none 120 125 125 150 162 120 125 150 Right Hand Side Ranges Constraint Lower Limit Current Value Upper Limit 1 100 108 123.75 2 57 120 none 3 8 25 58 4 41.5 50 54 -a) By how much can the amount of space decrease before there is a change in the profit? b) By how much can the amount of space decrease before there is a change in the product mix? c) By how much can the amount of time available to set up the display can increase before the solution (product mix) would change? d) What is the lowest value for the amount of time available to set up the display increase before the solution (product mix) would change?

Mallory Furniture buys two products for resale: big shelves (B) and medium shelves (M). Each big shelf costs $500 and requires 100 cubic feet of storage space, and each medium shelf costs $300 and requires 90 cubic feet of storage space. The company has $75,000 to invest in shelves this week, and the warehouse has 18,000 cubic feet available for storage. Profit for each big shelf is $300 and for each medium shelf is $150. -Which of the following is not a feasible purchase combination?

Given the following linear programming problem that minimizes cost: Min Z = 2x + 8y Subject to (1) 8x + 4y ? 64       (2) 2x + 4y ? 32       (3) y ? 2 -What is the sensitivity range for the third constraint, y ≥ 2?

Taco Loco is considering a new addition to their menu. They have test marketed a number of possibilities and narrowed them down to three new products, X, Y, and Z. Each of these products is made from a different combination of beef, beans, and cheese, and each product has a price point. Taco Loco feels they can sell an X for $17, a Y for $13, and a Z for $14. The company's management science consultant formulates the following linear programming model for company management. Max R = 14Z + 13Y + 17X subject to: Beef 2Z + 3Y + 4X ≤ 28 Cheese 9Z + 8Y + 11X ≤ 80 Beans 4Z + 4Y + 2X ≤ 68 X,Y,Z ≥ 0 The sensitivity report from the computer model reads as follows: $\text { Variable Cells }$ Cell Name Final Value Reduced Cost Objective Coefficient Allowable Increase Allowable Decrease \C \4 1.45 0 14 0.63 5.33 \D \4 Y 8.36 0 13 8 0.56 \E \4 0 -0.818 17 0.818 1+30 $\text { Constraints }$ Cell Name Final Value Shadow Price Constraint R.H. Side Allowable Increase Allowable Decrease \F \6 Beef 28 0.45 28 2 10.22 \F \7 Cheese 80 1.45 80 46 5.33 \F \8 Beans 39.27 0 68 1+30 28.73 -Taco Loco will make the same quantity of X, Y, and Z if the amount of cheese at their disposal is between ________ pounds and ________ pounds.

The sensitivity range for an objective function coefficient is the range of values over which the profit does not change.

The sensitivity range for a constraint quantity value is also the range over which the ________ is valid.

What combination of x and y is a feasible solution that minimizes the value of the objective function? Min Z = 3x + 15y    (1) 2x + 4y ? 12    (2) 5x + 2y ?10

The sensitivity range for a constraint quantity value is the range over which the optimal values of the decision variables do not change.

Tracksaws, Inc. makes tractors and lawn mowers. The firm makes a profit of $30 on each tractor and $30 on each lawn mower, and they sell all they can produce. The time requirements in the machine shop, fabrication, and tractor assembly are given in the table. Machine Shop Fabrication Assembly Tractor 2 hours 2 hours 1 hour Lawn Mower 1 hour 3 hours 0 hour Hrs. Available 60 hours 120 hours 45 hours Formulation: Let x = number of tractors produced per period y = number of lawn mowers produced per period MAX 30x+30y subject to 2x+y\leq60 2x+3y\leq120 x\leq45 The graphical solution is shown below. -What is the maximum amount a manager would be willing to pay for one additional hour of machining time?

A plant manager is attempting to determine the production schedule of various products to maximize profit. Assume that a machine hour constraint is binding. If the original amount of machine hours available is 200 minutes., and the range of feasibility is from 130 minutes to 300 minutes, providing two additional machine hours will result in

For the constraints given below, which point is in the feasible region of this minimization problem?    (1) 14x + 6y ? 42    (2) x + 3y ? 6

The reduced cost (shadow price) for a positive decision variable is ________.

Sensitivity analysis can be used to determine the effect on the solution for changing several parameters at once.

When the right-hand sides of two constraints are both increased by one unit, the value of the objective function will be adjusted by the sum of the constraints' prices.

Taco Loco is considering a new addition to their menu. They have test marketed a number of possibilities and narrowed them down to three new products, X, Y, and Z. Each of these products is made from a different combination of beef, beans, and cheese, and each product has a price point. Taco Loco feels they can sell an X for $17, a Y for $13, and a Z for $14. The company's management science consultant formulates the following linear programming model for company management. Max R = 14Z + 13Y + 17X subject to: Beef 2Z + 3Y + 4X ≤ 28 Cheese 9Z + 8Y + 11X ≤ 80 Beans 4Z + 4Y + 2X ≤ 68 X,Y,Z ≥ 0 The sensitivity report from the computer model reads as follows: $\text { Variable Cells }$ Cell Name Final Value Reduced Cost Objective Coefficient Allowable Increase Allowable Decrease \C \4 1.45 0 14 0.63 5.33 \D \4 Y 8.36 0 13 8 0.56 \E \4 0 -0.818 17 0.818 1+30 $\text { Constraints }$ Cell Name Final Value Shadow Price Constraint R.H. Side Allowable Increase Allowable Decrease \F \6 Beef 28 0.45 28 2 10.22 \F \7 Cheese 80 1.45 80 46 5.33 \F \8 Beans 39.27 0 68 1+30 28.73 -Taco Loco should try to purchase additional ________, but should not buy more ________.

The linear programming problem whose output follows is used to determine how many bottles of red nail polish (x1), blue nail polish (x2), green nail polish (x3), and pink nail polish (x4) a beauty salon should stock. The objective function measures profit; it is assumed that every piece stocked will be sold. Constraint 1 measures display space in units, constraint 2 measures time to set up the display in minutes. Note that green nail polish does not require any time to prepare its display. Constraints 3 and 4 are marketing restrictions. Constraint 3 indicates that the maximum demand for red and green polish is 25 bottles, while constraint 4 specifies that the minimum demand for blue, green, and pink nail polish bottles combined is at least 50 bottles. MAX $100 x _ { 1 } + 120 x _ { 2 } + 150 x _ { 3 } + 125 x _ { 4 }$ Subject to 1 . $x _ { 1 } + 2 x _ { 2 } + 2 x _ { 3 } + 2 x _ { 4 } \leq 108$ 2. $3 x _ { 1 } + 5 x _ { 2 } + x _ { 4 } \leq 120$ 3. $x _ { 1 } + x _ { 3 } \leq 25$ 4. $x _ { 2 } + x _ { 3 } + x _ { 4 } \geq 50$ $x _ { 1 } , x _ { 2 } , x _ { 3 } , x _ { 4 } \geq 0$ Optimal Solution: Objective Function Value = 7475.000 Variable Value Reduced Costs 8 0 0 5 17 0 33 0 Constraint Slack/ Surplus Dual Prices 1 0 75 2 63 0 3 0 25 4 0 -25 Objective Coefficient Ranges Variable Lower Limit Current Value Upper Limit 87.5 100 none none 120 125 125 150 162 120 125 150 Right Hand Side Ranges Constraint Lower Limit Current Value Upper Limit 1 100 108 123.75 2 57 120 none 3 8 25 58 4 41.5 50 54 -You are offered the chance to obtain more space. The offer is for 15 units and the total price is $1500. What should you do? Why?

Mallory Furniture buys two products for resale: big shelves (B) and medium shelves (M). Each big shelf costs $500 and requires 100 cubic feet of storage space, and each medium shelf costs $300 and requires 90 cubic feet of storage space. The company has $75,000 to invest in shelves this week, and the warehouse has 18,000 cubic feet available for storage. Profit for each big shelf is $300 and for each medium shelf is $150. -If the Mallory Furniture company decides to purchase 150 big shelves and no medium shelves, which of the two resources will be left over?