Exam 3: Linear Programming: Computer Solution and Sensitivity Analysis

Taco Loco is considering a new addition to their menu. They have test marketed a number of possibilities and narrowed them down to three new products, X, Y, and Z. Each of these products is made from a different combination of beef, beans, and cheese, and each product has a price point. Taco Loco feels they can sell an X for $17, a Y for $13, and a Z for $14. The company's management science consultant formulates the following linear programming model for company management. Max R = 14Z + 13Y + 17X subject to: Beef 2Z + 3Y + 4X ≤ 28 Cheese 9Z + 8Y + 11X ≤ 80 Beans 4Z + 4Y + 2X ≤ 68 X,Y,Z ≥ 0 The sensitivity report from the computer model reads as follows: $\text { Variable Cells }$ Cell Name Final Value Reduced Cost Objective Coefficient Allowable Increase Allowable Decrease \C \4 1.45 0 14 0.63 5.33 \D \4 Y 8.36 0 13 8 0.56 \E \4 0 -0.818 17 0.818 1+30 $\text { Constraints }$ Cell Name Final Value Shadow Price Constraint R.H. Side Allowable Increase Allowable Decrease \F \6 Beef 28 0.45 28 2 10.22 \F \7 Cheese 80 1.45 80 46 5.33 \FS 8 Beans 39.27 0 68 1+30 28.73 -What is the increase in revenue if Taco Loco purchases 20 pounds of cheese for $1 and uses it optimally?

The production manager for the Whoppy soft drink company is considering the production of two kinds of soft drinks: regular (R) and diet (D). The company operates one 8-hour shift per day. Therefore, the production time is 480 minutes per day. During the production process, one of the main ingredients, syrup, is limited to maximum production capacity of 675 gallons per day. Production of a regular case requires 2 minutes and 5 gallons of syrup, while production of a diet case needs 4 minutes and 3 gallons of syrup. Profits for regular soft drink are $3.00 per case and profits for diet soft drink are $2.00 per case. The formulation for this problem is given below. MAX Z = $3R + $2D s.t.    2R + 4D ? 480    5R + 3D ? 675 The sensitivity report is given below. Adjustable Cells Cell Name Final Value Reduced Cost Objective Coefficient Allowable Increase Allowable Decrease \ \ 6 Regular =90.00 0.00 3 0.33 2 \ \ 6 Diet =75.00 0.00 2 4 0.2 Constraints Cell Name Final Value Shadow Price Constraint R.H. Side Allowable Increase Allowable Decrease \ \ 3 Production (minutes) 480.00 0.07 480 420 210 text E \ 4 Syrup (gallons) 675.00 0.57 675 525 315 -if the company decides to increase the amount of syrup it uses during production of these soft drinks to 990 lbs. will the current product mix change? If show what is the impact on profit?

The accepted sequence for sensitivity analysis is objective function, left-hand side, and right-hand side.

Billy's Blues sells 3 types of T-shirts: Astro, Bling, and Curious. Manufacturing Astros requires 2 minutes of machine time and 20 minutes of labor, and costs $10. Brand Bling requires 2.5 minutes of machine time and 30 minutes of labor, and costs $14 to produce. Brand Curious requires 3 minutes of machine time and 45 minutes of labor, and costs $18 to produce. There are 300 machining hours available per week, 3750 labor hours, and he has a budget of $3000. Brand Astro sells for $15, Brand Bling for $18, and Brand Curious for $25. The LP formulation that maximizes week profit shown below. MAX 15A +18B + 25 C s.t.    2A + 2.5B + 3C ? 300    20A + 30B + 45C ? 3750    10A + 14B + 18C ? 3000 The solution from QM for Windows is show below. 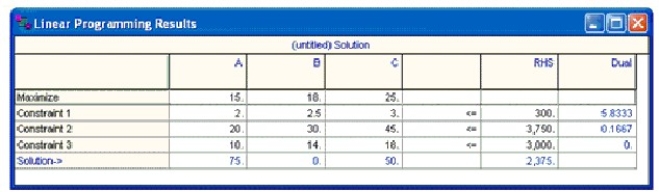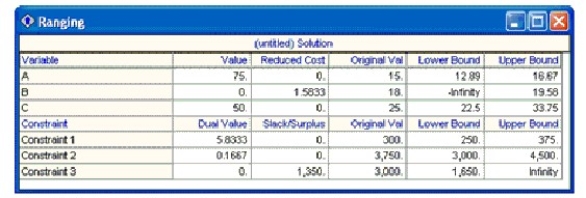-If Billy could acquire more of any resource, which would it be?

For a profit maximization problem, if the allowable increase for a coefficient in the objective function is infinite, then profits are unbounded.

The linear programming problem whose output follows is used to determine how many bottles of red nail polish (x1), blue nail polish (x2), green nail polish (x3), and pink nail polish (x4) a beauty salon should stock. The objective function measures profit; it is assumed that every piece stocked will be sold. Constraint 1 measures display space in units, constraint 2 measures time to set up the display in minutes. Note that green nail polish does not require any time to prepare its display. Constraints 3 and 4 are marketing restrictions. Constraint 3 indicates that the maximum demand for red and green polish is 25 bottles, while constraint 4 specifies that the minimum demand for blue, green, and pink nail polish bottles combined is at least 50 bottles. MAX $100 x _ { 1 } + 120 x _ { 2 } + 150 x _ { 3 } + 125 x _ { 4 }$ Subject to 1 . $x _ { 1 } + 2 x _ { 2 } + 2 x _ { 3 } + 2 x _ { 4 } \leq 108$    2. $3 x _ { 1 } + 5 x _ { 2 } + x _ { 4 } \leq 120$    3. $x _ { 1 } + x _ { 3 } \leq 25$    4. $x _ { 2 } + x _ { 3 } + x _ { 4 } \geq 50$     $x _ { 1 } , x _ { 2 } , x _ { 3 } , x _ { 4 } \geq 0$ Optimal Solution: Objective Function Value = 7475.000 Variable Value Reduced Costs 8 0 0 5 17 0 33 0 Constraint Slack/ Surplus Dual Prices 1 0 75 2 63 0 3 0 25 4 0 -25 Objective Coefficient Ranges Variable Lower Limit Current Value Upper Limit 87.5 100 none none 120 125 125 150 162 120 125 150 Right Hand Side Ranges Constraint Lower Limit Current Value Upper Limit 1 100 108 123.75 2 57 120 none 3 8 25 58 4 41.5 50 54 -How much space will be left unused? How many minutes of idle time remain for setting up the display?

The production manager for Beer etc. produces two kinds of beer: light (L) and dark (D). Two resources used to produce beer are malt and wheat. The manager can obtain at most 4800 oz of malt per week and at most 3200 oz of wheat per week, respectively. Each bottle of light beer requires 12 oz of malt and 4 oz of wheat, while a bottle of dark beer uses 8 oz of malt and 8 oz of wheat. Profits for light beer are $2 per bottle, and profits for dark beer are $1 per bottle. -Which of the following is not a feasible solution?

The production manager for the Whoppy soft drink company is considering the production of two kinds of soft drinks: regular and diet. The company operates one 8-hour shift per day. Therefore, the production time is 480 minutes per day. During the production process, one of the main ingredients, syrup, is limited to maximum production capacity of 675 gallons per day. Production of a regular case requires 2 minutes and 5 gallons of syrup, while production of a diet case needs 4 minutes and 3 gallons of syrup. Profits for regular soft drink are $3.00 per case and profits for diet soft drink are $2.00 per case. -Which of the following is not a feasible production combination?

Taco Loco is considering a new addition to their menu. They have test marketed a number of possibilities and narrowed them down to three new products, X, Y, and Z. Each of these products is made from a different combination of beef, beans, and cheese, and each product has a price point. Taco Loco feels they can sell an X for $17, a Y for $13, and a Z for $14. The company's management science consultant formulates the following linear programming model for company management. Max R = 14Z + 13Y + 17X subject to: Beef 2Z + 3Y + 4X ≤ 28 Cheese 9Z + 8Y + 11X ≤ 80 Beans 4Z + 4Y + 2X ≤ 68 X,Y,Z ≥ 0 The sensitivity report from the computer model reads as follows: $\text { Variable Cells }$ Cell Name Final Value Reduced Cost Objective Coefficient Allowable Increase Allowable Decrease \C \4 1.45 0 14 0.63 5.33 \D \4 Y 8.36 0 13 8 0.56 \E \4 0 -0.818 17 0.818 1+30 $\text { Constraints }$ Cell Name Final Value Shadow Price Constraint R.H. Side Allowable Increase Allowable Decrease \F \6 Beef 28 0.45 28 2 10.22 \F \7 Cheese 80 1.45 80 46 5.33 \F \8 Beans 39.27 0 68 1+30 28.73 -For humanitarian reasons, Taco Loco decides they would rather make product X than product Y. The dollar amount that they can both increase the price of Y and reduce the price of X by to accomplish this reversal of demand is ________.

Max Z = 5x1 + 3x2 Subject to: 6x1 + 2x2 ? 18    15x1 + 20x2 ? 60    x1, x2 ? 0 Determine the sensitivity range for each constraint.

Aunt Anastasia operates a small business: she produces seasonal ceramic objects to sell to tourists. For the spring, she is planning to make baskets, eggs, and rabbits. Based on your discussion with your aunt you construct the following table: $\begin{array} { l c c c c } \text { Product } & \begin{array} { c } \text { Mix/mold } \\\text { requirements (lb) }\end{array} & \begin{array} { c } \text { Kiln } \\\text { (units) }\end{array} & \begin{array} { c } \text { Paint \& Seal } \\\text { (hr) }\end{array} & \begin{array} { c } \text { Profit/product } \\\text { (\$) }\end{array} \\\hline \text { Baskets } & 0.500 & 1 & 0.250 & \$ 2.50 \\\text { Eggs } & 0.333 & 1 & 0.333 & \$ 1.50 \\\text { Rabbits } & 0.250 & 1 & 0.750 & \$ 2.00 \\\text { Capacity } & 20 \text { pounds } & 50 \text { units } & 80 \text { hours } & \\\hline\end{array}$ Your aunt also has committed to make 25 rabbits for a charitable organization. Based on the information in the table, you formulate the problem as a linear program. B = number of baskets produced E = number of eggs produced R = number of rabbits produced MAX 2.5B + 1.5E + 2R s.t. 0.5B + 0.333E + 0.25R ≤ 20 B + E + R ≤ 50 0.25B + 0.333E + 0.75R ≤ 80 R ≥ 25 The Excel solution and the answer and sensitivity report are shown below. The Answer Report: Target Cell (Max) Cell Name Original Value Final Value \ C\ 21 Profit 0 \ 112.5 $\text { Adjustable Cells }$ Cell Name Original Value Final Value \ C\ 18 Baskets 0 25 \ C\ 19 Eggs 0 0 \ C\ 20 Rabbits 0 25 $\text { Constraints }$ Cell Name Cell Value Formula Status Slack Not \G \1 3 Mix/mold 18.75 \G \1 3<= \F \1 3 Binding 1.25 \G \1 4 Kiln 50 \G \1 4<= \F \1 4 Binding 0 Not \G \1 5 Paint and Seal 25 \G \1 5<= \F \1 5 Binding 55 \G \1 6 Demand 25 \G \1 6>= \F \1 6 Binding 0 The Sensitivity Report: $\text { Adjustable Cells }$ Cell Name Final Value Reduced Cost Objective Coefficient Allowable Increase Allowable Decrease \ C\ 18 Baskets 25 0 2.5 1+30 0.5 \C \1 9 Eggs 0 -1 1.5 1 1+30 \C \2 0 Rabbits 25 0 2 0.5 1+30 $\text { Constraints }$ Cell Name Final Value Shadow Price Constraint R.H. Side Allowable Increase Allowable Decrease \ G\ 13 Mix/mold 18.75 0 20 1+30 1.25 \ G\ 14 Kiln 50 2.5 50 2.5 25 \ G\ 15 Paint and Seal 25 0 80 1+30 55 \G \1 6 Demand 25 -0.5 25 25 5 -Aunt Anastasia's available hours for paint and seal have fallen from 80 hours to 60 hours because of other commitments. How will this affect her profits?

The production manager for the Whoppy soft drink company is considering the production of two kinds of soft drinks: regular (R) and diet (D). The company operates one 8-hour shift per day. Therefore, the production time is 480 minutes per day. During the production process, one of the main ingredients, syrup, is limited to maximum production capacity of 675 gallons per day. Production of a regular case requires 2 minutes and 5 gallons of syrup, while production of a diet case needs 4 minutes and 3 gallons of syrup. Profits for regular soft drink are $3.00 per case and profits for diet soft drink are $2.00 per case. The formulation for this problem is given below. MAX Z = $3R + $2D s.t.    2R + 4D ? 480    5R + 3D ? 675 The sensitivity report is given below. Adjustable Cells Cell Name Final Value Reduced Cost Objective Coefficient Allowable Increase Allowable Decrease \ \ 6 Regular =90.00 0.00 3 0.33 2 \ \ 6 Diet =75.00 0.00 2 4 0.2 Constraints Cell Name Final Value Shadow Price Constraint R.H. Side Allowable Increase Allowable Decrease \ \ 3 Production (minutes) 480.00 0.07 480 420 210 text E \ 4 Syrup (gallons) 675.00 0.57 675 525 315 -What is the sensitivity range for the per-case profit of a diet soft drink?

The production manager for the Whoppy soft drink company is considering the production of two kinds of soft drinks: regular and diet. The company operates one 8-hour shift per day. Therefore, the production time is 480 minutes per day. During the production process, one of the main ingredients, syrup, is limited to maximum production capacity of 675 gallons per day. Production of a regular case requires 2 minutes and 5 gallons of syrup, while production of a diet case needs 4 minutes and 3 gallons of syrup. Profits for regular soft drink are $3.00 per case and profits for diet soft drink are $2.00 per case. -For the production combination of 135 regular cases and 0 diet cases, which resource is completely used up (at capacity)?

Because the management science model requires that parameters are known with certainty, sensitivity analysis is not used in practical, real-world applications of linear programming.

Billy's Blues sells 3 types of T-shirts: Astro, Bling, and Curious. Manufacturing Astros requires 2 minutes of machine time and 20 minutes of labor, and costs $10. Brand Bling requires 2.5 minutes of machine time and 30 minutes of labor, and costs $14 to produce. Brand Curious requires 3 minutes of machine time and 45 minutes of labor, and costs $18 to produce. There are 300 machining hours available per week, 3750 labor hours, and he has a budget of $3000. Brand Astro sells for $15, Brand Bling for $18, and Brand Curious for $25. The LP formulation that maximizes week profit shown below. MAX 15A +18B + 25 C s.t. 2A + 2.5B + 3C ≤ 300 20A + 30B + 45C ≤ 3750 10A + 14B + 18C ≤ 3000 The solution from QM for Windows is show below. -Billy's accountant made an error, and the budget has been reduced from $3000 to $2500. Billy's profit will go down by:

Aunt Anastasia operates a small business: she produces seasonal ceramic objects to sell to tourists. For the spring, she is planning to make baskets, eggs, and rabbits. Based on your discussion with your aunt you construct the following table: $\begin{array} { l c c c c } \text { Product } & \begin{array} { c } \text { Mix/mold } \\\text { requirements (lb) }\end{array} & \begin{array} { c } \text { Kiln } \\\text { (units) }\end{array} & \begin{array} { c } \text { Paint \& Seal } \\\text { (hr) }\end{array} & \begin{array} { c } \text { Profit/product } \\\text { (\$) }\end{array} \\\hline \text { Baskets } & 0.500 & 1 & 0.250 & \$ 2.50 \\\text { Eggs } & 0.333 & 1 & 0.333 & \$ 1.50 \\\text { Rabbits } & 0.250 & 1 & 0.750 & \$ 2.00 \\\text { Capacity } & 20 \text { pounds } & 50 \text { units } & 80 \text { hours } & \\\hline\end{array}$ Your aunt also has committed to make 25 rabbits for a charitable organization. Based on the information in the table, you formulate the problem as a linear program. B = number of baskets produced E = number of eggs produced R = number of rabbits produced MAX 2.5B + 1.5E + 2R s.t.    0.5B + 0.333E + 0.25R ? 20    B + E + R ? 50    0.25B + 0.333E + 0.75R ? 80    R ? 25 The Excel solution and the answer and sensitivity report are shown below. The Answer Report: Target Cell (Max) Cell Name Original Value Final Value \ C\ 21 Profit 0 \ 112.5 $\text { Adjustable Cells }$ Cell Name Original Value Final Value \ C\ 18 Baskets 0 25 \ C\ 19 Eggs 0 0 \ C\ 20 Rabbits 0 25 $\text { Constraints }$ Cell Name Cell Value Formula Status Slack Not \G \1 3 Mix/mold 18.75 \G \1 3<= \F \1 3 Binding 1.25 \G \1 4 Kiln 50 \G \1 4<= \F \1 4 Binding 0 Not \G \1 5 Paint and Seal 25 \G \1 5<= \F \1 5 Binding 55 \G \1 6 Demand 25 \G \1 6>= \F \1 6 Binding 0 The Sensitivity Report: $\text { Adjustable Cells }$ Cell Name Final Value Reduced Cost Objective Coefficient Allowable Increase Allowable Decrease \ C\ 18 Baskets 25 0 2.5 1+30 0.5 \C \1 9 Eggs 0 -1 1.5 1 1+30 \C \2 0 Rabbits 25 0 2 0.5 1+30 $\text { Constraints }$ Cell Name Final Value Shadow Price Constraint R.H. Side Allowable Increase Allowable Decrease \ G\ 13 Mix/mold 18.75 0 20 1+30 1.25 \ G\ 14 Kiln 50 2.5 50 2.5 25 \ G\ 15 Paint and Seal 25 0 80 1+30 55 \G \1 6 Demand 25 -0.5 25 25 5 -Suppose the charitable organization contacted Aunt Anastasia and told her that they had underestimated the amount of rabbits they needed. Instead of 25 rabbits, they need 35. How would this affect Aunt Anastasia's profits?

The production manager for the Whoppy soft drink company is considering the production of two kinds of soft drinks: regular (R) and diet (D). The company operates one 8-hour shift per day. Therefore, the production time is 480 minutes per day. During the production process, one of the main ingredients, syrup, is limited to maximum production capacity of 675 gallons per day. Production of a regular case requires 2 minutes and 5 gallons of syrup, while production of a diet case needs 4 minutes and 3 gallons of syrup. Profits for regular soft drink are $3.00 per case and profits for diet soft drink are $2.00 per case. The formulation for this problem is given below. MAX Z = $3R + $2D s.t.    2R + 4D ? 480    5R + 3D ? 675 The sensitivity report is given below. Adjustable Cells Cell Name Final Value Reduced Cost Objective Coefficient Allowable Increase Allowable Decrease \ \ 6 Regular =90.00 0.00 3 0.33 2 \ \ 6 Diet =75.00 0.00 2 4 0.2 Constraints Cell Name Final Value Shadow Price Constraint R.H. Side Allowable Increase Allowable Decrease \ \ 3 Production (minutes) 480.00 0.07 480 420 210 text E \ 4 Syrup (gallons) 675.00 0.57 675 525 315 -What is the sensitivity range of the production time?

Taco Loco is considering a new addition to their menu. They have test marketed a number of possibilities and narrowed them down to three new products, X, Y, and Z. Each of these products is made from a different combination of beef, beans, and cheese, and each product has a price point. Taco Loco feels they can sell an X for $17, a Y for $13, and a Z for $14. The company's management science consultant formulates the following linear programming model for company management. Max R = 14Z + 13Y + 17X subject to: Beef 2Z + 3Y + 4X ≤ 28 Cheese 9Z + 8Y + 11X ≤ 80 Beans 4Z + 4Y + 2X ≤ 68 X,Y,Z ≥ 0 The sensitivity report from the computer model reads as follows: $\text { Variable Cells }$ Cell Name Final Value Reduced Cost Objective Coefficient Allowable Increase Allowable Decrease \C \4 1.45 0 14 0.63 5.33 \D \4 Y 8.36 0 13 8 0.56 \E \4 0 -0.818 17 0.818 1+30 $\text { Constraints }$ Cell Name Final Value Shadow Price Constraint R.H. Side Allowable Increase Allowable Decrease \F \6 Beef 28 0.45 28 2 10.22 \F \7 Cheese 80 1.45 80 46 5.33 \F \8 Beans 39.27 0 68 1+30 28.73 -Taco Loco should produce both ________ but should not make any ________.

For a maximization problem, the shadow price measures the ________ in the value of the optimal solution, per unit increase for a given ________.

Max Z = 5x1 + 3x2 Subject to:  6x1 + 2x2 ? 18    15x1 + 20x2 ? 60    x1, x2 ? 0 Determine the sensitivity range for each objective function coefficient.