Exam 7: Using Binary Integer Programming to Deal With Yes-Or-No Decisions

Note: This problem requires the use of a linear programming application such as Solver or Analytic Solver. Your employer is trying to select from a list of possible capital projects. The projects, along with their cost and benefits, are listed below. The capital budget available is $1 million. In addition to spending constraints, your employer would like to select at least two projects. If project 1 is chosen then project 2 cannot be selected. Formulate the problem as a linear program and determine the optimal solution. Project Cost Net Presert Value Notes 1 \ 250,000 \ 500,000 Carrnot be selected if 2 is selected 2 \ 500,000 \ 750,000 Carrot be selected if 1 is selected 3 \ 290,000 \ 333,000 4 \ 650,000 \ 400,000 5 \ 750,000 \ 600,000

A firm has prepared the following binary integer program to evaluate a number of potential new capital projects. The firm's goal is to maximize the net present value of their decision while not spending more than their currently available capital. Max 100x1 + 120x2 + 90x3 + 135x4 s.t. 150x1 + 200x2 + 225x3 + 175x4 ? 500 {Constraint 1} X1 + x2 + x3 + x4 ? 2 {Constraint 2} X2 + x4 ? 1 {Constraint 3} X2 + x3 ? 1 {Constraint 4} X1 = x4 {Constraint 5} $x _ { j } = \left\{ \begin{array} { l } 1 , \text { if project } j \text { is selected } \\0 , \text { otherwise }\end{array} \right.$ Which of the constraints enforces a mutually exclusive relationship?

Note: This problem requires the use of a linear programming application such as Solver or Analytic Solver. A firm has prepared the following binary integer program to evaluate a number of potential locations for new warehouses. The firm's goal is to maximize the net present value of their decision while not spending more than their currently available capital. Max 20x1 + 30x2 + 10x3 + 15x4 s.t. 5x1 + 7x2 + 12x3 + 11x4 ? 21 {Constraint 1} X1 + x2 + x3 + x4 ? 2 {Constraint 2} X1 + x2 ? 1 {Constraint 3} X1 + x3 ? 1 {Constraint 4} X2 = x4 {Constraint 5} $x _ { j } = \left\{ \begin{array} { l } 1 , \text { if location } j \text { is selected } \\0 , \text { otherwise }\end{array} \right.$ Set up the problem in Excel and find the optimal solution. What is the expected net present value of the optimal solution?

BIP can be used to determine the timing of activities.

In a BIP problem, 1 corresponds to a yes decision and 0 to a no decision. If project A can be undertaken only if project B is also undertaken then the following constraint needs to be added to the formulation:

The university is scheduling cleaning crews for its ten buildings. Each crew has a different cost and is qualified to clean only certain buildings. There are eight possible crews to choose from in this case. The goal is to minimize costs while making sure that each building is cleaned. The management science department formulated the following linear programming model to help with the selection process. Min200x1 + 250x2 + 225x3 + 190x4 +215x5 + 245x6 + 235x7 + 220x8 s.t. x1 + x2 + x5 + x7 ? 1 {Building A constraint} X1 + x2 + x3 ? 1 {Building B constraint} X6 + x8 ? 1 {Building C constraint} X1 + x4 + x7 ? 1 {Building D constraint} X2 + x7 ? 1 {Building E constraint} X3 + x8 ? 1 {Building F constraint} X2 + x5 + x7 ? 1 {Building G constraint} X1 + x4 + x6 ? 1 {Building H constraint} X1 + x6 + x8 ? 1 {Building I constraint} X1 + x2 + x7 ? 1 {Building J constraint} $x _ { j } = \left\{ \begin{array} { l } 1 , \text { if crew } j \text { is selected } \\0 , \text { otherwise }\end{array} \right.$ Which of the crews can be scheduled to clean building A?

A new pizza restaurant is moving into town. The owner is considering a number of potential sites and would like to minimize the initial investment involved with purchasing locations. However, the owner is very concerned about delivery time and wants to make sure that every neighborhood in the city can have a pizza delivered in 15 minutes or less. The owner has divided the city into 10 neighborhoods (A-J) and is currently considering a total of 8 different locations. To help with the decision, the owner formulated the following linear programming model: Min 100x1 + 120x2 + 90x3 + 135x4 +75x5 + 85x6 + 110x7 + 135x8 s.t. x1 + x2 + x5 + x7 ? 1 {Neighborhood A constraint} X1 + x2 + x3 ? 1 {Neighborhood B constraint} X5 + x6 + x8 ? 1 {Neighborhood C constraint} X1 + x4 + x7 ? 1 {Neighborhood D constraint} X2 + x3 + x7 ? 1 {Neighborhood E constraint} X3 + x4 + x8 ? 1 {Neighborhood F constraint} X2 + x5 + x7 ? 1 {Neighborhood G constraint} X1 + x4 + x6 ? 1 {Neighborhood H constraint} X1 + x6 + x8 ? 1 {Neighborhood I constraint} X1 + x2 + x7 ? 1 {Neighborhood J constraint} $x _ { j } = \left\{ \begin{array} { l } 1 , \text { if location } j \text { is selected } \\0 , \text { otherwise }\end{array} \right.$ Which of the locations is the most expensive?

The university is scheduling cleaning crews for its ten buildings. Each crew has a different cost and is qualified to clean only certain buildings. There are eight possible crews to choose from in this case. The goal is to minimize costs while making sure that each building is cleaned. The management science department formulated the following linear programming model to help with the selection process. Min 200x1 + 250x2 + 225x3 + 190x4 +215x5 + 245x6 + 235x7 + 220x8 s.t. x1 + x2 + x5 + x7 ? 1 {Building A constraint} X1 + x2 + x3 ? 1 {Building B constraint} X6 + x8 ? 1 {Building C constraint} X1 + x4 + x7 ? 1 {Building D constraint} X2 + x7 ? 1 {Building E constraint} X3 + x8 ? 1 {Building F constraint} X2 + x5 + x7 ? 1 {Building G constraint} X1 + x4 + x6 ? 1 {Building H constraint} X1 + x6 + x8 ? 1 {Building I constraint} X1 + x2 + x7 ? 1 {Building J constraint} $x _ { j } = \left\{ \begin{array} { l } 1 , \text { if crew } j \text { is selected } \\0 , \text { otherwise }\end{array} \right.$ Which of the constraints is a set covering constraint?

Note: This problem requires the use of a linear programming application such as Solver or Analytic Solver. To enhance the safety of your facility, you decide to add more fire extinguishers. Your goal is to have each area within 50 feet of a fire extinguisher, but to minimize the total number of fire extinguishers you need to purchase. You have divided the facility into 7 zones and have identified 8 possible locations for fire extinguishers. The following table shows the distance (in feet) from each zone to each potential location. 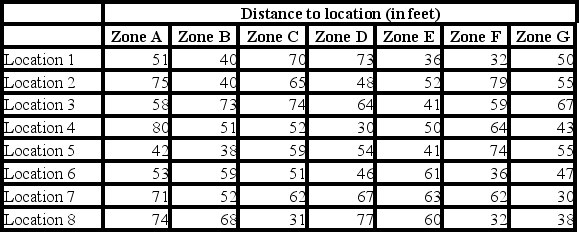How many fire extinguishers should you purchase?

In a BIP problem with 3 mutually exclusive alternatives, x1, x2, and x3, the following constraint needs to be added to the formulation:

Binary variables are best suited to be the decision variables when dealing with yes-or-no decisions.

The constraint x1 ≤ x2 in a BIP problem means that alternative 2 cannot be selected unless alternative 1 is also selected.

A new pizza restaurant is moving into town. The owner is considering a number of potential sites and would like to minimize the initial investment involved with purchasing locations. However, the owner is very concerned about delivery time and wants to make sure that every neighborhood in the city can have a pizza delivered in 15 minutes or less. The owner has divided the city into 10 neighborhoods (A-J) and is currently considering a total of 8 different locations. To help with the decision, the owner formulated the following linear programming model: Min 100x1 + 120x2 + 90x3 + 135x4 +75x5 + 85x6 + 110x7 + 135x8 s.t.x1 + x2 + x5 + x7 ? 1 {Neighborhood A constraint} X1 + x2 + x3 ? 1 {Neighborhood B constraint} X5 + x6 + x8 ? 1 {Neighborhood C constraint} X1 + x4 + x7 ? 1 {Neighborhood D constraint} X2 + x3 + x7 ? 1 {Neighborhood E constraint} X3 + x4 + x8 ? 1 {Neighborhood F constraint} X2 + x5 + x7 ? 1 {Neighborhood G constraint} X1 + x4 + x6 ? 1 {Neighborhood H constraint} X1 + x6 + x8 ? 1 {Neighborhood I constraint} X1 + x2 + x7 ? 1 {Neighborhood J constraint} $x _ { j } = \left\{ \begin{array} { l } 1 , \text { if location } j \text { is selected } \\0 , \text { otherwise }\end{array} \right.$ Which of the constraints is a set covering constraint?

In a BIP problem, 1 corresponds to a yes decision and 0 to a no decision. If there are two projects under consideration, A and B, and either both projects will be undertaken or no project will be undertaken, then the following constraint needs to be added to the formulation:

The constraint x1 + x2 + x3­ ≤ 3 in a BIP represents mutually exclusive alternatives.

In a site selection problem, a common goal is to identify the set of locations that provides adequate service at the minimum cost.

The university administration would like to add some additional parking locations. To make everyone happy, they would like each building to be within a 5 minute walk of one set of new parking spaces (the spaces will be added in blocks of 10 parking spaces). The university is considering six locations for the new parking spaces, but would like to minimize the overall cost of the project. In addition to the walking time requirement, the university would like to add at least 40 new parking spaces (at least 4 blocks of 10). To help with the decision, the management science department formulated the following linear programming model: Min 400x1 + 375x2 + 425x3 + 350x4 +410x5 + 500x6 S.t. x1 + x2 + x5 + x6 ? 1 {Residence Hall A constraint} X1 + x2 + x3 ? 1 {Residence Hall B constraint} X4 + x5 + x6 ? 1 {Science building constraint} X1 + x4 + x5 ? 1 {Music building constraint} X2 + x3 + x4 ? 1 {Math building constraint} X3 + x4 + x5 ? 1 {Business building constraint} X2 + x5 + x6 ? 1 {Auditorium constraint} X1 + x4 + x6 ? 1 {Arena constraint} X1 + x2 + x3 + x4 + x5 + x6 ? 4 {Total locations constraint} $x _ { j } = \left\{ \begin{array} { l } 1 , \text { if project } j \text { is selected } \\0 , \text { otherwise }\end{array} \right.$ Which of the constraints is a set covering constraint? I. Residence Hall A constraint. II. Science building constraint. III. Total locations constraint.

A yes-or-no decision is a mutually exclusive decision if it can be yes only if a certain other yes-or-no decision is yes.

A linear programming formulation is not valid for a product mix problem when there are setup costs for initiating production.

Note: This problem requires the use of a linear programming application such as Solver or Analytic Solver. A new pizza restaurant is moving into town. The owner is considering a number of potential sites and would like to minimize the initial investment involved with purchasing locations. However, the owner is very concerned about delivery time and wants to make sure that every neighborhood in the city can have a pizza delivered in 15 minutes or less. The owner has divided the city into 10 neighborhoods (A-J) and is currently considering a total of 8 different locations. To help with the decision, the owner formulated the following linear programming model: Min 100x1 + 120x2 + 90x3 + 135x4 +75x5 + 85x6 + 110x7 + 135x8 s.t. x1 + x2 + x5 + x7 ? 1 {Neighborhood A constraint} X1 + x2 + x3 ? 1 {Neighborhood B constraint} X5 + x6 + x8 ? 1 {Neighborhood C constraint} X1 + x4 + x7 ? 1 {Neighborhood D constraint} X2 + x3 + x7 ? 1 {Neighborhood E constraint} X3 + x4 + x8 ? 1 {Neighborhood F constraint} X2 + x5 + x7 ? 1 {Neighborhood G constraint} X1 + x4 + x6 ? 1 {Neighborhood H constraint} X1 + x6 + x8 ? 1 {Neighborhood I constraint} X1 + x2 + x7 ? 1 {Neighborhood J constraint} $x _ { j } = \left\{ \begin{array} { l } 1 , \text { if location } j \text { is selected } \\0 , \text { otherwise }\end{array} \right.$ Set up the problem in Excel and find the optimal solution. Which locations are selected?