Exam 15: A:nonparametric Statistics

A one-sample t test is the parametric counterpart of the Kruskal-Wallis test.

In a normal approximation to the sign test, the standardized test statistic is calculated as z = -1.58. To test the alternative hypothesis that the location of population 1 is to left of the location of population 2, what would be the p-value of the test?

We can safely employ nonparametric tests even when we know nothing at all about the populations from which sample data are being drawn.

In testing 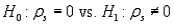at the 5% significance level, a sample of size 20 is used. In this case, what is the rejection region?

The Wilcoxon rank sum test statistic T is approximately normally distributed whenever the sample sizes are larger than or equal to which of these values?

Nonparametric methods can be applied to a wider variety of s because they have less rigid requirements than parametric methods.

Which one of the following is a disadvantage of the sign test?

You are performing the Wilcoxon rank sum test. The 13th through 15th values in an ordered array of pooled sample data all equal $180 (while the 12th value is less and the 16th value is more). What are the appropriate ranks for the three $180 values?

The Kruskal-Wallis test statistic can be approximated by a chi-square distribution with k - 1 degrees of freedom (where k is the number of populations) whenever the sample sizes are all greater than or equal to which of the following values?

In which of the following situations might the Wilcoxon signed-rank test be more appropriate than the paired-difference t test?

The Wilcoxon rank sum test is a nonparametric test that measures the degree of association between two variables for which only rank-order data are available.

Which of these tests is a nonparametric method to compare two populations when the samples are matched pairs and the data are interval, and where the normality requirement necessary to perform the parametric test is unsatisfied?

The Wilcoxon rank sum test is a nonparametric test that can be used to compare two independent samples when the assumptions for a t test are invalid.

The significance level for a Wilcoxon signed-rank sum test is 0.05. The alternative hypothesis is stated as: The location of population 1 is different from the location of population 2. Given this information, what is the appropriate critical value for a sample of size 20 ?

In a normal approximation to the Wilcoxon signed-rank test, the test statistic is calculated as z = 1.36. For a two-tailed test, what is the p-value?

Under which of the following conditions are nonparametric tests appropriate for quantitative data?

The sign test, or Wilcoxon signed-rank test, is a nonparametric test that can be used to compare two dependent samples when the assumptions for a t test are invalid.

Which of the following is a nonparametric alternative to the Kruskal-Wallis test for differences in more than two medians?

When the direction (and not the magnitude) of the difference within each matched paired in a paired experiment is known, the sign test can be used while the Wilcoxon signed-rank test cannot be used.

The Spearman rank correlation coefficient is calculated by first ranking the data values, and then calculating the Pearson correlation coefficient of the ranks.