Exam 8: Large-Sample Estimation
Exam 1: Describing Data With Graphs134 Questions
Exam 2: Describing Data With Numerical Measures235 Questions
Exam 3: Describing Bivariate Data57 Questions
Exam 4: A: probability and Probability Distributions107 Questions
Exam 4: B: probability and Probability Distributions157 Questions
Exam 5: Several Useful Discrete Distributions166 Questions
Exam 6: The Normal Probability Distribution235 Questions
Exam 7: Sampling Distributions231 Questions
Exam 8: Large-Sample Estimation187 Questions
Exam 9: A: large-Sample Tests of Hypotheses154 Questions
Exam 9: B: large-Sample Tests of Hypotheses106 Questions
Exam 10: A: Inference From Small Samples192 Questions
Exam 10: B: Inference From Small Samples124 Questions
Exam 11: A: The Analysis of Variance136 Questions
Exam 11: B: The Analysis of Variance137 Questions
Exam 12: A: linear Regression and Correlation131 Questions
Exam 12: B: linear Regression and Correlation171 Questions
Exam 13: Multiple Regression Analysis232 Questions
Exam 14: Analysis of Categorical Data158 Questions
Exam 15: A:nonparametric Statistics139 Questions
Exam 15: B:nonparametric Statistics95 Questions
Select questions type
One-sided confidence bounds can be constructed for the population mean 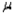 and population proportion p, but not for
and population proportion p, but not for 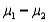 (the difference between population means) or
(the difference between population means) or 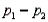 (the difference between population proportions).
(the difference between population proportions).
Free
(True/False)
4.8/5  (37)
(37)
Correct Answer:
False
A lawn service owner is testing new environmentally friendly weed killers. He discovers that a particular weed killer is effective 89% of the time. Suppose that this estimate was based on a random sample of 60 applications. Construct a 90% confidence interval for p, the true proportion of weeds killed by this particular brand.
Free
(Essay)
4.8/5  (43)
(43)
Correct Answer:
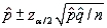 = 0.89
= 0.89 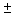 (1.645)
(1.645) 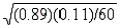 = 0.89
= 0.89 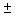 0.07 (0.82, 0.96)
0.07 (0.82, 0.96)
An experiment was conducted to compare two diets A and B, designed for weight reduction. Two groups of 50 overweight dieters each were randomly selected. One group was placed on diet A and the other on diet B, and their weight losses were recorded over a 30-day period. The means and standard deviations of the weight-loss measurements (in kg) for the two groups are shown in the table.  Find a 95% confidence interval for the difference in mean weight loss for the two diets. Interpret your confidence interval.
Find a 95% confidence interval for the difference in mean weight loss for the two diets. Interpret your confidence interval.
Free
(Essay)
4.8/5  (28)
(28)
Correct Answer:
The 95% confidence interval for 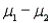 is approximated by
is approximated by 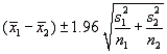 = (10.7- 7.1)
= (10.7- 7.1) 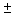 1.96 (0.1935) = 3.6
1.96 (0.1935) = 3.6 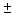 0.37926, or 3.22074 <
0.37926, or 3.22074 < 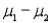 < 3.97926 kg.
< 3.97926 kg.
One can estimate with 95% confidence that the difference in the mean weight loss for the two diets is roughly between 3.22 and 3.98 kg. In repeated sampling, all intervals constructed in this manner will enclose ( 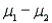 ) 95% of the time. Hence, we are fairly certain that this particular interval encloses
) 95% of the time. Hence, we are fairly certain that this particular interval encloses 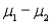 .
.
Ground Beef Weights Narrative
The meat department of a local supermarket packages ground beef using meat trays of two sizes: one designed to hold approximately 700 g of meat, and a larger one that holds approximately 1.4 kg. A random sample of 36 packages of the smaller meat trays produced weight measurements with an average of 715 g and a standard deviation of 90 g.
-Refer to Ground Beef Weights Narrative. Suppose that the quality control department of this supermarket chain intends that the amount of ground beef in the smaller trays should be 700 g on average. Should the confidence interval above concern the quality control department? Explain.
(Essay)
4.8/5  (41)
(41)
An airline executive estimates that 25% of all flights arrive late. How many flights must we include in a simple random sample if we want to be 90% confident that the true population proportion of flights that arrive late lies within 0.01 of our sample proportion? Justify your conclusion.
(Essay)
5.0/5  (34)
(34)
Given that n = 49, 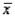 = 75, and
= 75, and 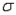 = 7, the lower and upper limits of the 68.26% confidence interval for the population mean
= 7, the lower and upper limits of the 68.26% confidence interval for the population mean 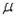 are 74 and 76, respectively.
are 74 and 76, respectively.
(True/False)
5.0/5  (38)
(38)
Two independent random samples of sizes 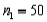 and
and 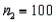 have been selected from binomial populations with respective parameters
have been selected from binomial populations with respective parameters 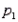 and
and 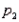 , resulting in 38 and 65 successes, respectively. Then, the point estimation of the difference
, resulting in 38 and 65 successes, respectively. Then, the point estimation of the difference 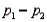 is -27.
is -27.
(True/False)
4.8/5  (31)
(31)
The error of estimation is the difference between a statistic computed from a sample and the corresponding parameter computed from the population.
(True/False)
4.8/5  (35)
(35)
The error of estimation is the distance between an estimate and the estimated parameter.
(True/False)
4.8/5  (28)
(28)
After constructing a confidence interval estimate for a population mean, you believe that the interval is useless because it is too wide. In order to correct this , what should you do?
(Multiple Choice)
4.9/5  (39)
(39)
Random sample of n = 1000 observations from a binomial population produced x = 728 successes. Estimate the binomial proportion p and calculate the margin of error.
(Essay)
4.7/5  (29)
(29)
One way to reduce the margin of error in a confidence interval is to decrease the confidence coefficient.
(True/False)
4.9/5  (37)
(37)
Why do those who engage in estimation insist on random sampling, rather than convenience sampling or judgment sampling?
(Multiple Choice)
4.8/5  (32)
(32)
A quality control engineer wants to determine what is the proportion of defective parts coming off the assembly line. Past experiments, based on large sample sizes, have shown this proportion to be 0.19. What sample size does the engineer need in order to estimate, with 90% confidence, this proportion with a margin of error of 0.12? Justify your conclusion.
(Essay)
4.9/5  (37)
(37)
Which of the following best describes the term "margin of error"?
(Multiple Choice)
4.9/5  (28)
(28)
Two independent random samples of sizes 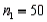 and
and 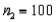 have been selected from binomial populations with respective parameters
have been selected from binomial populations with respective parameters 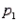 and
and 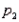 , resulting in 38 and 65 successes, respectively. Then the standard error of
, resulting in 38 and 65 successes, respectively. Then the standard error of 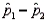 is estimated as 0.077.
is estimated as 0.077.
(True/False)
4.8/5  (34)
(34)
Increasing the confidence level for a confidence interval estimate for the difference between two population means, with all other things held constant, will result in a wider confidence interval estimate.
(True/False)
4.8/5  (20)
(20)
A parent believes the average height for 14-year-old girls differs from that of 14-year-old boys. Estimate the difference in height between girls and boys, using a 95% confidence interval. The summary data are listed below. Based on your interval, do you think there is a significant difference between the true mean height of 14-year-old girls and boys? Explain.
14-year-old girls' summary data: 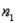 = 40,
= 40, 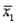 = 155 cm,
= 155 cm, 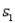 = 6.1 cm
14-year-old boys' summary data:
= 6.1 cm
14-year-old boys' summary data: 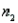 = 40,
= 40, 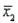 = 146 cm,
= 146 cm, 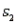 = 9.1 cm
= 9.1 cm
(Essay)
4.8/5  (39)
(39)
Suppose a 95% confidence interval for the mean height of a 12-year-old male in Canada is 137 to 165 cm. In repeated sampling, 95% of the intervals constructed will contain the interval from 137 to 165 cm.
(True/False)
4.9/5  (34)
(34)
If we wish to construct a 95% confidence interval estimate for the difference between two population proportions, what would the confidence level be?
(Multiple Choice)
5.0/5  (38)
(38)
Showing 1 - 20 of 187
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)