Exam 8: Probability Distributions and Statistics
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
A new drug has been found to be effective in treating 85% of the people afflicted by a certain disease. If the drug is administered to 300 people who have this disease, what are the mean and the standard deviation of the number of people for whom the drug can be expected to be effective?
Round the answers to the nearest hundredth if necessary. 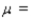 __________
__________ 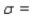 __________
__________
(Short Answer)
4.9/5  (39)
(39)
An examination consisting of ten true-or-false questions was taken by a class of 100 students. The probability distribution of the random variable X, where X denotes the number of questions answered correctly by a randomly chosen student, is represented by the accompanying histogram. The rectangle with base centered on the number 8 is missing. What should be the height of this rectangle?
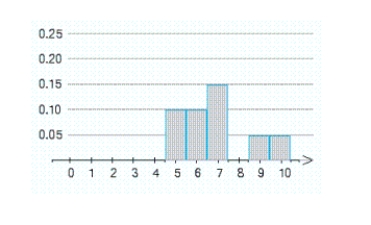
height = __________
height = __________
(Short Answer)
4.9/5  (28)
(28)
Use the appropriate normal distribution to approximate the resulting binomial distribution.
A basketball player has a 75% chance of making a free throw. What is the probability of her making 85 or more free throws in 120 trials?
Round your answer to four decimal places, if necessary.
The probability is __________.
(Short Answer)
4.8/5  (43)
(43)
The probability distribution of the random variable X is shown in the accompanying table. 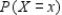 Find the following, rounded to two decimal places, if necessary.
Find the following, rounded to two decimal places, if necessary. 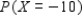 __________
__________ 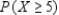 __________
__________ 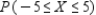 __________
__________ 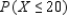 __________
__________
(Essay)
4.7/5  (40)
(40)
An advertisement for brand A chicken noodle soup claims that 60% of all consumers prefer brand A over other brands, the chief competitor's product. To test this claim, David Horowitz, host of The Consumer Advocate, selected ten people at random from the audience. After tasting both soups, each person was asked to state his or her preference. Assuming the company's claim is correct, find the probability 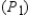 that the company's claim was supported by the experiment; that is, six or more people stated a preference for brand A. Then find the probability
that the company's claim was supported by the experiment; that is, six or more people stated a preference for brand A. Then find the probability 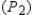 the company's claim was not supported by the experiment; that is, fewer than six people stated a preference for brand A?
the company's claim was not supported by the experiment; that is, fewer than six people stated a preference for brand A?
(Multiple Choice)
4.8/5  (38)
(38)
In an examination given to a class of 20 students, the test scores were obtained as following. 
 Find the mean, or average, score.
__________
Find the mode.
__________
Find the median score.
__________
Which of these three measures of central tendency do you think is the least representative of the set of scores?
__________
Find the mean, or average, score.
__________
Find the mode.
__________
Find the median score.
__________
Which of these three measures of central tendency do you think is the least representative of the set of scores?
__________
(Short Answer)
4.8/5  (28)
(28)
The probability distribution of a random variable X is  Compute the mean, variance, and standard deviation of X.
Round your answers to the nearest hundredth, if necessary.
Compute the mean, variance, and standard deviation of X.
Round your answers to the nearest hundredth, if necessary. 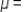
 __________
Var (X) =
__________
__________
Var (X) =
__________ 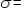 __________
__________
(Essay)
4.7/5  (35)
(35)
Roger Hunt intends to purchase one of two car dealerships currently for sale in a certain city. Records obtained from each of the two dealers reveal that their weekly volume of sales, with corresponding probabilities, are as follows.
Dahl Motors 
 Farthington Auto Sales
Farthington Auto Sales  The average profit/car at Dahl Motors is $364, and the average profit/car at Farthington Auto Sales is $436.
Find the average number of cars sold each week at Dahl Motors. Give your answer to two decimal places, if necessary.
__________
Find the average number of cars sold each week at Farthington Auto Sales. Give your answer to two decimal places, if necessary.
__________
If Roger's objective is to purchase the dealership that generates the higher weekly profit, which dealership should he purchase? (Compare the expected weekly profit for each dealership.)
__________
The average profit/car at Dahl Motors is $364, and the average profit/car at Farthington Auto Sales is $436.
Find the average number of cars sold each week at Dahl Motors. Give your answer to two decimal places, if necessary.
__________
Find the average number of cars sold each week at Farthington Auto Sales. Give your answer to two decimal places, if necessary.
__________
If Roger's objective is to purchase the dealership that generates the higher weekly profit, which dealership should he purchase? (Compare the expected weekly profit for each dealership.)
__________
(Short Answer)
4.8/5  (33)
(33)
Three balls are selected at random without replacement from an urn containing four green balls and six red balls. Let the random variable X denote the number of green balls drawn. List the outcomes of the experiment.
(Essay)
4.8/5  (37)
(37)
Use the appropriate normal distribution to approximate the resulting binomial distribution.
A fair coin is tossed 25 times. What is the probability of obtaining more than 12 heads? (Round your intermediate calculations to 2 decimal places.)
(Multiple Choice)
4.9/5  (32)
(32)
Use the appropriate normal distribution to approximate the resulting binomial distribution.
Jorge sells magazine subscriptions over the phone. He estimates that the probability of his making a sale with each attempt is .12. What is the probability of Jorge making more than 10 sales if he makes 80 calls?
(Multiple Choice)
4.9/5  (33)
(33)
Find the expected value of a random variable X having the following probability distribution: 
(Multiple Choice)
4.7/5  (35)
(35)
In American roulette a player may bet on a split (two adjacent numbers). In this case, if the player bets $1 and either number comes up, the player wins $14 and gets his $1 back. If neither comes up, he loses his $1 bet. Find the expected value of the winnings on a $1 bet placed on a split. Round your answer to the nearest cent.
(Multiple Choice)
4.8/5  (33)
(33)
Find the value of the probability of the standard normal variable Z corresponding to this area. 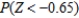
(Multiple Choice)
4.9/5  (30)
(30)
The manager of a certain toy company has decided to accept a shipment of electronic games if none of a random sample of 30 is found to be defective. What is the probability 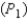 that he will accept the shipment if 10% of the electronic games is defective? What is the probability
that he will accept the shipment if 10% of the electronic games is defective? What is the probability  that he will accept the shipment if 5% of the electronic games is defective? Round your answers to three decimal places, if necessary.
that he will accept the shipment if 5% of the electronic games is defective? Round your answers to three decimal places, if necessary.  = __________
= __________  = __________
= __________
(Short Answer)
4.9/5  (39)
(39)
Determine whether the table gives the probability distribution of the random variable X. Explain your answer. 
(Multiple Choice)
4.8/5  (33)
(33)
A Christmas tree light has an expected life of 200 hr and a standard deviation of 3 hr. Suppose 190,000 of these Christmas tree lights are used by a large city as part of its Christmas decorations. Estimate the number of lights that will require replacement between 185 and 215 hr of use.
(Multiple Choice)
4.8/5  (39)
(39)
An examination consisting of ten true-or-false questions was taken by a class of 100 students. The probability distribution of the random variable X, where X denotes the number of questions answered correctly by a randomly chosen student, is represented by the accompanying histogram. The rectangle with base centered on the number 8 is missing. What should be the height of this rectangle? 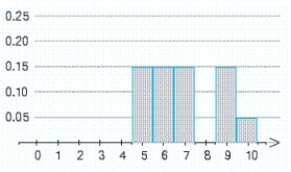
(Multiple Choice)
4.9/5  (42)
(42)
The general manager of the Service Department of a television company has estimated that the time that elapses between the dates of purchase and the dates on which the 19-inch sets manufactured by the company first require service is normally distributed with a mean of 22 mo and a standard deviation of 4 months. If the company gives a 1-year warranty on parts and labor for these sets, determine the percentage of sets manufactured and sold by the company that may require service before the warranty period runs out.
Round your answer to the nearest hundredth, if necessary.
__________ %
(Short Answer)
4.8/5  (40)
(40)
A bank has two automatic tellers at its main office and two at each of its three branches. The number of machines that break down on a given day, along with the corresponding probabilities, are shown in the following table. Find the expected number of machines that will break down on a given day. Give your answer to two decimal places, if necessary.  E = __________
E = __________
(Short Answer)
4.9/5  (30)
(30)
Showing 21 - 40 of 263
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)