Exam 17: Markov Processes
Exam 1: Introduction61 Questions
Exam 2: Introduction to Probability54 Questions
Exam 3: Probability Distributions84 Questions
Exam 4: Decision Analysis69 Questions
Exam 5: Utility Game Theory56 Questions
Exam 6: Time Series Analysis Forecasting46 Questions
Exam 7: Intro to Linear Programming49 Questions
Exam 8: LP Sensitivity Analysis59 Questions
Exam 9: LP Applications60 Questions
Exam 10: Distribution Network Models68 Questions
Exam 11: Integer Linear Programming61 Questions
Exam 12: Advanced Optimization Applications56 Questions
Exam 13: Project Scheduling58 Questions
Exam 14: Inventory Models68 Questions
Exam 15: Waiting Line Models66 Questions
Exam 16: Simulation62 Questions
Exam 17: Markov Processes41 Questions
Select questions type
In Markov analysis,we are concerned with the probability that the
(Multiple Choice)
4.7/5  (38)
(38)
For a situation with weekly dining at either an Italian or Mexican restaurant,
(Multiple Choice)
4.8/5  (42)
(42)
A state i is a transient state if there exists a state j that is reachable from i,but the state i is not reachable from state j.
(True/False)
4.7/5  (32)
(32)
If the probability of making a transition from a state is 0,then that state is called a(n)
(Multiple Choice)
4.9/5  (41)
(41)
Give two examples of how Markov analysis can aid decision making.
(Short Answer)
4.7/5  (38)
(38)
The probability of reaching an absorbing state is given by the
(Multiple Choice)
4.9/5  (38)
(38)
If an absorbing state exists,then the probability that a unit will ultimately move into the absorbing state is given by the steady state probability.
(True/False)
4.9/5  (41)
(41)
Rent-To-Keep rents household furnishings by the month.At the end of a rental month a customer can: a)rent the item for another month,b)buy the item,or c)return the item.The matrix below describes the month-to-month transition probabilities for 32-inch stereo televisions the shop stocks.
What is the probability that a customer who rented a TV this month will eventually buy it?
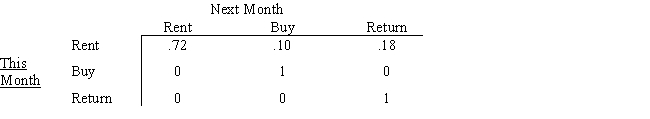
(Essay)
4.9/5  (51)
(51)
Henry,a persistent salesman,calls North's Hardware Store once a week hoping to speak with the store's buying agent,Shirley.If Shirley does not accept Henry's call this week,the probability she will do the same next week is .35.On the other hand,if she accepts Henry's call this week,the probability she will not do so next week is .20.
a.Construct the transition matrix for this problem.
b.How many times per year can Henry expect to talk to Shirley?
c.What is the probability Shirley will accept Henry's next two calls if she does not accept his call this week?
d.What is the probability of Shirley accepting exactly one of Henry's next two calls if she accepts his call this week?
(Essay)
4.9/5  (33)
(33)
What assumptions are necessary for a Markov process to have stationary transition probabilities?
(Short Answer)
4.8/5  (37)
(37)
A unique matrix of transition probabilities should be developed for each customer.
(True/False)
4.8/5  (39)
(39)
If a Markov chain has at least one absorbing state,steady-state probabilities cannot be calculated.
(True/False)
4.7/5  (43)
(43)
The probability of going from state 1 in period 2 to state 4 in period 3 is
(Multiple Choice)
4.8/5  (39)
(39)
Showing 21 - 40 of 41
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)