Question 1

Given the opportunity, a rational decision-maker should always select the alternative with the:

Accepted Answer

A)  greatest expected return regardless of risk. 
B)  lowest expected return regardless of risk. 
C)  greatest expected utility. 
D)  lowest probability of occurrence. 
E)  greatest marginal utility. 
A)  greatest expected return regardless of risk. 
B)  lowest expected return regardless of risk. 
C)  greatest expected utility. 
D)  lowest probability of occurrence. 
E)  greatest marginal utility. C

Question 2

You are offered a choice between two lotteries, K and L:
Lottery K: You win $1,000 with complete certainty.
Lottery L: You win: $5,000 with probability .10
$1,000 with probability .75
$0 with probability .15
Compute the expected value of both lotteries, and indicate which you would choose. Explain your choice, using the concept of certainty equivalent.

Accepted Answer

The expected value of K is $1,000. The expected value of L is: (.1)($5,000) +
(.75)($1,000) = $1,250. Even though L has the greater expected value, a sufficiently riskaverse person will lean toward choosing Lottery K; the certain $1,000 is preferred to the risk of L (an appreciable chance of receiving nothing).

Question 3

Suppose that Rick is fortunate enough to receive a gift from a family member of $5,000, which he may use as he does see fit. Rick is then offered a chance to receive an additional $2,000 with certainty, or a 50-50 chance of either $5,000 or $0.
(a) Which would Rick accept?
(b) Suppose instead that Rick has $10,000 in a bank account. He must now choose between
paying $3,000 with certainty or taking a 50-50 chance of loss of either $0 or $5,000. Which would Rick choose?
(c) Were Rick’s choices consistent? Explain why or why not.

Accepted Answer

a.A risk-neutral person prefers the gamble. However, the size of the risk and
prevailing risk aversion means that empirically about 65% of experimental subjects choosethe sure $2,000.
b.Rick has to accept the gamble, reasoning that he can afford the loss (still retain $5,000), and hope for no loss ($10,000), rather than settle for $7,000.
c.It is inconsistent to take the certain choice in part (a) and to gamble in part (b). In each case, the certain outcome is $7,000, while gambling amounts to a 50-50 risk of $5,000 and $10,000. Though the risky choices in parts (a) and (b) are identical, the different "framing" of the risks can cause the Rick to see them differently and make different, inconsistent decisions.

Question 4

Apply the expected-value criterion to choose between these investments.
Investment A has possible outcomes: $100,000 (50% chance), $40,000 (30% chance), and $50,000 (20% chance). Investment B has possible outcomes: $150,000, $60,000, $20,000, and $80,000 with each outcome equally likely.

Accepted Answer

Expected value of investment A = E(V_A) =

Question 5

A risky outcome's expected value is:

Accepted Answer

A)  the value of the most likely outcome. 
B)  the mid-point of the extreme (high and low) possible values. 
C)  the degree of dispersion of the possible outcomes. 
D)  the sum of the products of the probabilities of all outcomes and their values. 
E)  the equally-weighted average of all outcomes. 
A)  the value of the most likely outcome. 
B)  the mid-point of the extreme (high and low) possible values. 
C)  the degree of dispersion of the possible outcomes. 
D)  the sum of the products of the probabilities of all outcomes and their values. 
E)  the equally-weighted average of all outcomes.

Question 6

How are certainty equivalent and attitude toward risk related? Illustrate with an example.

Accepted Answer

The certainty equivalent is the amount o

Question 7

Firm X is currently selling a consumer good and faces two related decisions, one with respect to pricing and the other with respect to marketing. With respect to pricing, it can maintain its "standard" price or it can adopt a lower "discount" price. With respect to marketing, it can keep with its current advertising campaign or it can expand its advertising. The main risk facing the firm concerns the course of the economy in the near-term: whether the economy will continue healthy growth or whether it will experience a recession. The table below shows the firm's possible profit results (in $ millions) depending on its price and advertising actions. Finally, the firm judges that there is an 80% chance of growth and a 20% chance of a recession.
 $\begin{array}{lcc}
&\text { Growing}&\text { Recession }\
&\text { Economy}&\
\text { Standard P + Level Ads } & 25 & -20 \
\text { Discount P + Level Ads } & 15 & 0 \
\text { Standard P + Increased } & 30 & -45 \
\text { Ads } & & \
\text { Discount P + Increased } & 20 & -10\
\text { Ads } & & 
\end{array}$

(a) Firm X must make its decision now (before knowing the future course of the economy). Which of the four alternatives maximizes its expected profit?

Accepted Answer

The decision tree is:
 @#IMG-DLM& According to the

Question 8

If a decision is made on the basis of expected utility, which of the two investments, investment R and investment C, should the decision-maker choose?

Accepted Answer

Expected utility obtained from investmen

Question 9

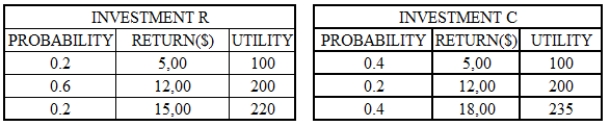
A chemical company is in the process of studying two long-term plans. The first plan involves expansion of their industrial division. The second plan emphasizes expansion in the business of consumer pharmaceuticals. Market research reveals the following (preliminary) results (returns are in $ millions):
 $\begin{array}{c}
\text {INDUSTRIAL}\
\text {EXPANSION}\
\begin{array}{cc}
\text { PROBABILITY } & \text { PROFITS } \
0.3 & 10 \
0.3 & 15 \
0.4 & 20
\end{array}
\end{array}$ $\begin{array}{c}
\text { PHARMACEUTICALS }\
\begin{array}{cc}
\text { PROBABILITY} &\text {PROFITS }\
0.2 & 0 \
0.3 & 10 \
0.3 & 20 \
0.2 & 40
\end{array}
\end{array}$  The planning committee has the (risk averse) utility function U = 10M - 0.05M2. Discuss the long-term planning decision based on the preliminary predictions and the given utility function:

Accepted Answer

Expansion of the industrial division see

Question 10

When there is multiple possible outcomes from a decision, the result is:

Accepted Answer

A)  a small margin of error in firm forecasts. 
B)  greater possible losses. 
C)  a significant degree of uncertainty. 
D)  lower overall risk. 
E)  greater expected returns. 
A)  a small margin of error in firm forecasts. 
B)  greater possible losses. 
C)  a significant degree of uncertainty. 
D)  lower overall risk. 
E)  greater expected returns.

Question 11

The accompanying figure shows the decision tree of an operations manager who is considering a new production technique. ER represents his expected return (in thousand $) from the new technique. If he does not adopt the technique his expected return would be zero. The probabilities of the technique being a success or a failure are .7 and .3 respectively. Compute the expected return (in thousand $) from the adoption of the new production technique.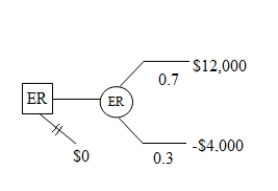

Accepted Answer

A)  $8,400 
B)  $1,000 
C)  -$2,000 
D)  $7,200 
E)  $8,000 
A)  $8,400 
B)  $1,000 
C)  -$2,000 
D)  $7,200 
E)  $8,000

Question 12

A convenient way to represent decisions, chance events, and possible outcomes in choices under risk and uncertainty is known as a:

Accepted Answer

A)  probability distribution. 
B)  decision table. 
C)  decision tree. 
D)  expected outcome tree. 
E)  risk table. 
A)  probability distribution. 
B)  decision table. 
C)  decision tree. 
D)  expected outcome tree. 
E)  risk table.

Question 13

If a fair coin is tossed 1,000 times, the frequency of heads will be close to:

Accepted Answer

A)  .6. 
B)  .5. 
C)  .3. 
D) .2. 
E)  There is not enough information to provide an answer. 
A)  .6. 
B)  .5. 
C)  .3. 
D) .2. 
E)  There is not enough information to provide an answer.

Question 14

Define probability with an example.

Accepted Answer

The probability of an outcome is the odd

Question 15

Which of the following is true of subjective probability?

Accepted Answer

A)  It is a measure of the historical frequency of an uncertain event. 
B)  It is a measure of the frequency of a certain event. 
C)  It represents the decision maker's best assessment, based on current information, of the likelihood of an uncertain event. 
D)  It represents an intuitive and ad hoc assessment. 
E)  It measures the degree of variation around the mean. 
A)  It is a measure of the historical frequency of an uncertain event. 
B)  It is a measure of the frequency of a certain event. 
C)  It represents the decision maker's best assessment, based on current information, of the likelihood of an uncertain event. 
D)  It represents an intuitive and ad hoc assessment. 
E)  It measures the degree of variation around the mean.

Question 16

An investor estimates the expected return of option A to be $180,000 and its expected utility to be 400. The expected return of option B is $120,000, and its expected utility is 450. The investor should:

Accepted Answer

A)  select option A because it has the higher expected return. 
B)  select option B because it has the higher expected utility. 
C)  select option A because 180,000/120,000 > 450/400. 
D)  be indifferent between option A and option B. 
E)  There is not enough information to answer this question. 
A)  select option A because it has the higher expected return. 
B)  select option B because it has the higher expected utility. 
C)  select option A because 180,000/120,000 > 450/400. 
D)  be indifferent between option A and option B. 
E)  There is not enough information to answer this question.

Question 17

An investment has the possibility of earning $10,000, $8,000 or $2,000 depending on the state of the economy that is prosperity, modern growth, and recession respectively. The probabilities of prosperity, moderate growth, and recession are .4, .3, and .3 respectively. The expected value of the investment is:

Accepted Answer

A)  $10,000. 
B)  $21,000. 
C)  $7,000. 
D)  $3,000. 
E)  $8,000. 
A)  $10,000. 
B)  $21,000. 
C)  $7,000. 
D)  $3,000. 
E)  $8,000.

Question 18

When taking risky decisions, a common pitfall that the managers face is:

Accepted Answer

A)  seeing too many possibilities. 
B)  holding pessimistic beliefs. 
C)  gathering too much information. 
D)  relying on verbal expressions of probability. 
E)  relying on the rules of thumb. 
A)  seeing too many possibilities. 
B)  holding pessimistic beliefs. 
C)  gathering too much information. 
D)  relying on verbal expressions of probability. 
E)  relying on the rules of thumb.

Question 19

Mary runs her own small business, and has a utility function for assets of:
U(A) = 22A - .07A2‚ for all 0≤ A ≤ 100, where A denotes total assets in thousands of dollars.
(a) Describe Mary's attitude toward risk.
(b) Assume that Mary's current asset holding are $20,000. Should she accept a business opportunity that has a probability of 0.55 leading to a net profit of $15,000 and a probability of 0.45 leading to a net loss of $15,000?
(c) Assume that Mary's assets are $85,000 instead. Should she now accept the same offer?
(d) Comment on the results of the previous two questions.

Accepted Answer

Mary shows increasing risk aversion. As

Question 20

Consider the following risky prospect: $\begin{array} { | c | c | c | } 
\hline \text { MONEY } & \text { UTLITY } & \text { PROBABILTTY } \
\hline \$ 20,000 & 10 & 0.2 \
\hline \$ 30,000 & 18 & 0.2 \
\hline \$ 40,000 & 24 & 0.6 \
\hline
\end{array}$ The expected utility is equal to:

Accepted Answer

A)  $30,000. 
B)  18. 
C)  20. 
D)  24. 
E)  $34,000. 
A)  $30,000. 
B)  18. 
C)  20. 
D)  24. 
E)  $34,000.

Given the opportunity, a rational decision-maker should always select the alternative with the:

Apply the expected-value criterion to choose between these investments. Investment A has possible outcomes: $100,000 (50% chance), $40,000 (30% chance), and $50,000 (20% chance). Investment B has possible outcomes: $150,000, $60,000, $20,000, and $80,000 with each outcome equally likely.

A risky outcome's expected value is:

How are certainty equivalent and attitude toward risk related? Illustrate with an example.

If a decision is made on the basis of expected utility, which of the two investments, investment R and investment C, should the decision-maker choose?

When there is multiple possible outcomes from a decision, the result is:

A convenient way to represent decisions, chance events, and possible outcomes in choices under risk and uncertainty is known as a:

If a fair coin is tossed 1,000 times, the frequency of heads will be close to:

Define probability with an example.

Which of the following is true of subjective probability?

An investor estimates the expected return of option A to be $180,000 and its expected utility to be 400. The expected return of option B is $120,000, and its expected utility is 450. The investor should:

When taking risky decisions, a common pitfall that the managers face is:

Consider the following risky prospect: MONEY UTLITY PROBABILTTY \ 20,000 10 0.2 \ 30,000 18 0.2 \ 40,000 24 0.6 The expected utility is equal to:

Introduction to Economic Decision Making

Optimal Decisions Using Marginal Analysis

Demand Analysis and Optimal Pricing

Estimating and Forecasting Demand

Production

Cost Analysis

Perfect Competition

Monopoly

Oligopoly

Game Theory and Competitive Strategy

Regulation, Public Goods, and Benefit-Cost Analysis

The Value of Information

Asymmetric Information and Organizational Design

Bargaining and Negotiation

Linear Programming

Auctions and Competitive Bidding Available Online

Filters

Exam 12: Decision Making Under Uncertainty

Given the opportunity, a rational decision-maker should always select the alternative with the:

Apply the expected-value criterion to choose between these investments. Investment A has possible outcomes: $100,000 (50% chance), $40,000 (30% chance), and $50,000 (20% chance). Investment B has possible outcomes: $150,000, $60,000, $20,000, and $80,000 with each outcome equally likely.

A risky outcome's expected value is:

How are certainty equivalent and attitude toward risk related? Illustrate with an example.

If a decision is made on the basis of expected utility, which of the two investments, investment R and investment C, should the decision-maker choose?

When there is multiple possible outcomes from a decision, the result is:

A convenient way to represent decisions, chance events, and possible outcomes in choices under risk and uncertainty is known as a:

If a fair coin is tossed 1,000 times, the frequency of heads will be close to:

Define probability with an example.

Which of the following is true of subjective probability?

An investor estimates the expected return of option A to be $180,000 and its expected utility to be 400. The expected return of option B is $120,000, and its expected utility is 450. The investor should:

When taking risky decisions, a common pitfall that the managers face is:

Consider the following risky prospect: MONEY UTLITY PROBABILTTY \ 20,000 10 0.2 \ 30,000 18 0.2 \ 40,000 24 0.6 The expected utility is equal to:

Introduction to Economic Decision Making

Optimal Decisions Using Marginal Analysis

Demand Analysis and Optimal Pricing

Estimating and Forecasting Demand

Production

Cost Analysis

Perfect Competition

Monopoly

Oligopoly

Game Theory and Competitive Strategy

Regulation, Public Goods, and Benefit-Cost Analysis

The Value of Information

Asymmetric Information and Organizational Design

Bargaining and Negotiation

Linear Programming

Auctions and Competitive Bidding Available Online

Filters