Question 1

What is true about threats in the game in Scenario 13.15?

Accepted Answer

A)  Simple can change the equilibrium by means of a credible threat; Boring cannot. 
B)  Boring can change the equilibrium by means of a credible threat; Simple cannot. 
C)  Boring can change the equilibrium by means of a credible threat only if it can move before Simple. 
D)  Simple can change the equilibrium by means of a credible threat only if it can move before Boring. 
E)  Neither firm has a credible threat with which to change this equilibrium. 
A)  Simple can change the equilibrium by means of a credible threat; Boring cannot. 
B)  Boring can change the equilibrium by means of a credible threat; Simple cannot. 
C)  Boring can change the equilibrium by means of a credible threat only if it can move before Simple. 
D)  Simple can change the equilibrium by means of a credible threat only if it can move before Boring. 
E)  Neither firm has a credible threat with which to change this equilibrium. E

Question 2

In the game in Scenario 13.10, there is:

Accepted Answer

A)  a mixed strategy equilibrium, and no other. 
B)  a mixed strategy and a pure strategy equilibrium. 
C)  a mixed strategy and two pure strategy equilibria. 
D)  a mixed strategy and four pure strategy equilibrium. 
E)  no equilibrium in either mixed or pure strategies. 
A)  a mixed strategy equilibrium, and no other. 
B)  a mixed strategy and a pure strategy equilibrium. 
C)  a mixed strategy and two pure strategy equilibria. 
D)  a mixed strategy and four pure strategy equilibrium. 
E)  no equilibrium in either mixed or pure strategies. A

Question 3

Two firms in a local market compete in the manufacture of cyberwidgets. Each firm must decide if they will engage in product research to innovate their version of the cyberwidget. The payoffs of each firm's strategy are a function of the strategy of their competitor as well. The payoff matrix is presented below.   Firm #2 chooses to innovate with probability 20/21. If Firm #1 does the same, what is the expected payoff? Is this a Mixed Strategy Nash Equilibrium? Suppose, instead, that firm #2 innovates with probability 2/3. Should player #1 always innovate?

Accepted Answer

If firm #1 does the same, the expected payoffs for both firms are zero. This is a Mixed Strategy Nash Equilibrium. If Firm #2 chooses to innovate with probability 2/3, Firm #1 should always innovate. This is because the expected profits are as high as possible when firm #1 sets the probability of choosing to innovate equal to 1.

Question 4

Consider the Matching Pennies game:   Suppose Player A always uses a pure strategy that selects heads. What is Player B's optimal response to this pure strategy?

Accepted Answer

A)  Always select heads. 
B)  Always select tails. 
C)  Mixed strategy with probability 1/2 on heads and 1/2 on tails 
D)  There is no optimal pure or mixed strategy for this situation. 
A)  Always select heads. 
B)  Always select tails. 
C)  Mixed strategy with probability 1/2 on heads and 1/2 on tails 
D)  There is no optimal pure or mixed strategy for this situation.

Question 5

Why does cooperative behavior break down in games with finite endpoints?

Accepted Answer

A)  Each player has an incentive to deviate from a cooperative strategy during the last period. 
B)  A Nash equilibrium in pure strategies is not possible in finite repeated games. 
C)  Finite games have the same outcomes as one-period games, and cooperation is not possible in one-period games. 
D)  A Nash equilibrium is only possible in mixed strategies in finite repeated games, but all of the probabilities assigned to particular strategies approach zero as the number of finite game periods becomes large. Thus, we cannot evaluate the expected payoffs in these games. 
A)  Each player has an incentive to deviate from a cooperative strategy during the last period. 
B)  A Nash equilibrium in pure strategies is not possible in finite repeated games. 
C)  Finite games have the same outcomes as one-period games, and cooperation is not possible in one-period games. 
D)  A Nash equilibrium is only possible in mixed strategies in finite repeated games, but all of the probabilities assigned to particular strategies approach zero as the number of finite game periods becomes large. Thus, we cannot evaluate the expected payoffs in these games.

Question 6

Two firms in a local market compete in the manufacture of cyberwidgets. Each firm must decide if they will offer a warranty or not. The payoffs of each firm's strategy are a function of their competitor as well. The payoff matrix is presented below.   Does either player have a dominant strategy? Does the game have any Nash equilibria? What is the maximin strategy of each player in the game? Should the players use a mixed strategy?

Accepted Answer

Both players have a dominant strategy to

Question 7

Scenario 13.3
Consider the following game:  
-In the game in Scenario 13.3, the equilibrium outcome:

Accepted Answer

A)  is for Moto to offer a CD changer and Zport to offer low-profile tires. 
B)  is for Moto to offer a CD changer and Zport to offer a sun roof. 
C)  is for Moto to offer free maintenance and Zport to offer low-profile tires. 
D)  is for Moto to offer free maintenance and Zport to offer a sunroof. 
E)  does not exist in pure strategies. 
A)  is for Moto to offer a CD changer and Zport to offer low-profile tires. 
B)  is for Moto to offer a CD changer and Zport to offer a sun roof. 
C)  is for Moto to offer free maintenance and Zport to offer low-profile tires. 
D)  is for Moto to offer free maintenance and Zport to offer a sunroof. 
E)  does not exist in pure strategies.

Question 8

In the game in Scenario 13.11, equilibrium is:

Accepted Answer

A)  R1, C1. 
B)  R1, C2. 
C)  R2, C1. 
D)  R2, C2. 
E)  a mixed strategy based on all four pure strategies. 
A)  R1, C1. 
B)  R1, C2. 
C)  R2, C1. 
D)  R2, C2. 
E)  a mixed strategy based on all four pure strategies.

Question 9

If Boring were able to move first in a sequential version of the game in Scenario 13.15, the equilibrium would be:

Accepted Answer

A)  an $80 price for Simple and a $70 price for Boring. 
B)  an $80 price for Simple and a $25 price for Boring. 
C)  a $35 price for Simple and a $70 price for Boring. 
D)  a $35 price for Simple and a $25 price for Boring. 
E)  a mixed strategy equilibrium. 
A)  an $80 price for Simple and a $70 price for Boring. 
B)  an $80 price for Simple and a $25 price for Boring. 
C)  a $35 price for Simple and a $70 price for Boring. 
D)  a $35 price for Simple and a $25 price for Boring. 
E)  a mixed strategy equilibrium.

Question 10

The countries Economus and Sociolomous on planet Subjectus are engaged in a Cold War. The payoffs of their available strategies are presented in the table below. 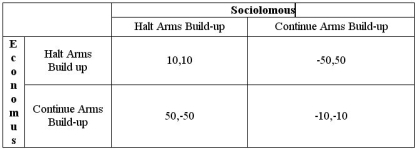  The payoffs are listed in terms of percentage growth in the standard of living of the two countries. Does either country have a dominant strategy? Does the game have a Nash equilibrium? What is the maximin strategy of each player in the game?

Accepted Answer

Both countries can do better by continui

Question 11

Scenario 13.6
Consider the following game. Payoffs are in millions of dollars.  
-In the game in Scenario 13.6,

Accepted Answer

A)  "Poison Pill" is a dominant strategy for Lawrence LLP. 
B)  "Dump" is a dominant strategy for Lawrence LLP. 
C)  "TurboTech" is a dominant strategy for ERS Co. 
D)  "ZamboniTech" is a dominant strategy for ERS Co. 
E)  No firm has a dominant strategy. 
A)  "Poison Pill" is a dominant strategy for Lawrence LLP. 
B)  "Dump" is a dominant strategy for Lawrence LLP. 
C)  "TurboTech" is a dominant strategy for ERS Co. 
D)  "ZamboniTech" is a dominant strategy for ERS Co. 
E)  No firm has a dominant strategy.

Question 12

La Tortilla is the only producer of tortillas in Santa Teresa. The firm produces 10,000 tortillas each day and has the capacity to increase production to 100,000 tortillas each day. La Tortilla has made a large profit for years, but no other firm has chosen to compete in the Santa Teresa tortilla market. La Tortilla has been able to deter entry because if other firms were to enter the market it would greatly step-up production and reduce price.

Accepted Answer

A)  La Tortilla's behavior is inconsistent with economic theory. 
B)  La Tortilla has been successful because of its credible threat. 
C)  La Tortilla behaves like a Stackelberg firm. 
D)  La Tortilla must have other barriers to entry to protect its monopoly power. 
A)  La Tortilla's behavior is inconsistent with economic theory. 
B)  La Tortilla has been successful because of its credible threat. 
C)  La Tortilla behaves like a Stackelberg firm. 
D)  La Tortilla must have other barriers to entry to protect its monopoly power.

Question 13

You are playing a game in which a dollar bill is auctioned. The highest bidder receives the dollar in return for the amount bid. However, the second-highest bidder must pay the amount that he or she bids, and gets nothing in return. The optimal strategy is:

Accepted Answer

A)  to bid the smallest allowable increment below $1. 
B)  to bid nothing. 
C)  to bid $0.99. 
D)  to bid more than a dollar. 
A)  to bid the smallest allowable increment below $1. 
B)  to bid nothing. 
C)  to bid $0.99. 
D)  to bid more than a dollar.

Question 14

Megan and Amanda are both 7 years old and operate lemonade stands. Megan lives on the east side of Welch Avenue while Amanda resides on the west side of Welch Avenue. Each morning, the girls must decide whether to place their stand on Welch Avenue or Lincoln Avenue. When they set their stand-up, they don't know what the other will do and can't relocate. If both girls put their stand on Welch, both girls receive $175 in profits. If both girls put their stand on Lincoln, they each receive $75 in profits. If one girl sets their stand on Welch while the other operates on Lincoln, the stand on Welch earns $300 in profits while the stand on Lincoln earns $225. Diagram the relevant payoff matrix. Does either girl have a dominant strategy? Does the game have a Nash equilibrium? What is the maximin strategy of each player in the game?

Accepted Answer

Neither player has a dominant strategy i

Question 15

Scenario 13.2
Consider the following game: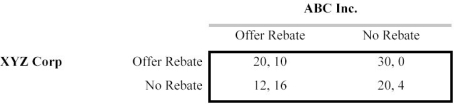  
-In the game in Scenario 13.2, the equilibrium strategies:

Accepted Answer

A)  are for both firms to offer rebates. 
B)  are for ABC to offer a rebate, and XYZ not to offer a rebate. 
C)  are for XYZ to offer a rebate, and ABC not to offer a rebate. 
D)  are for both firms to offer no rebate. 
E)  does not exist in pure strategies. 
A)  are for both firms to offer rebates. 
B)  are for ABC to offer a rebate, and XYZ not to offer a rebate. 
C)  are for XYZ to offer a rebate, and ABC not to offer a rebate. 
D)  are for both firms to offer no rebate. 
E)  does not exist in pure strategies.

Question 16

Consider the following game in which two firms decide how much of a homogeneous good to produce. The annual profit payoffs for each firm are stated in the cell of the game matrix, and Firm A's payoffs appear first in the payoff pairs:   What are the dominant strategies in this game?

Accepted Answer

A)  Both firms produce low levels of output. 
B)  Both firms produce high levels of output. 
C)  Firm A's dominant strategy is to produce low levels of output, but Firm B does not have a dominant strategy. 
D)  Firm B's dominant strategy is to produce low levels of output, but Firm A does not have a dominant strategy. 
E)  Neither firm has a dominant strategy. 
A)  Both firms produce low levels of output. 
B)  Both firms produce high levels of output. 
C)  Firm A's dominant strategy is to produce low levels of output, but Firm B does not have a dominant strategy. 
D)  Firm B's dominant strategy is to produce low levels of output, but Firm A does not have a dominant strategy. 
E)  Neither firm has a dominant strategy.

Question 17

A "sequential game" is:

Accepted Answer

A)  another term for a repeated game. 
B)  another term for a cooperative game. 
C)  the term for a game in which individuals receive their payoffs at different times. 
D)  the term for a game in which individuals do not commit to strategy choices at the same time. 
E)  the term for a game in which each outcome occurs, one after the other, as the game is repeated over time. 
A)  another term for a repeated game. 
B)  another term for a cooperative game. 
C)  the term for a game in which individuals receive their payoffs at different times. 
D)  the term for a game in which individuals do not commit to strategy choices at the same time. 
E)  the term for a game in which each outcome occurs, one after the other, as the game is repeated over time.

Question 18

Which of the following situations is likely to generate noncooperative behavior in repeated games?

Accepted Answer

A)  The game is repeated a finite number of times. 
B)  There are many players in the game. 
C)  The payoffs can change rapidly from one game period to the next. 
D)  All of these situations can generate noncooperative behavior. 
A)  The game is repeated a finite number of times. 
B)  There are many players in the game. 
C)  The payoffs can change rapidly from one game period to the next. 
D)  All of these situations can generate noncooperative behavior.

Question 19

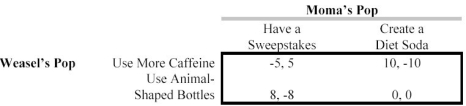Scenario 13.10
Consider the game below:  
-The game in Scenario 13.10 is:

Accepted Answer

A)  variable-sum. 
B)  constant-sum. 
C)  cooperative. 
D)  a Prisoners' Dilemma. 
E)  a Cournot Production Cross. 
A)  variable-sum. 
B)  constant-sum. 
C)  cooperative. 
D)  a Prisoners' Dilemma. 
E)  a Cournot Production Cross.

Question 20

Relative to a simultaneous-move situation, the gain to firm R from being able to move first in the game in Scenario 13.14, would be:

Accepted Answer

A)  40. 
B)  37. 
C)  32. 
D)  5. 
E)  3. 
A)  40. 
B)  37. 
C)  32. 
D)  5. 
E)  3.

What is true about threats in the game in Scenario 13.15?

In the game in Scenario 13.10, there is:

Consider the Matching Pennies game: Suppose Player A always uses a pure strategy that selects heads. What is Player B's optimal response to this pure strategy?

Why does cooperative behavior break down in games with finite endpoints?

Scenario 13.3 Consider the following game: -In the game in Scenario 13.3, the equilibrium outcome:

In the game in Scenario 13.11, equilibrium is:

If Boring were able to move first in a sequential version of the game in Scenario 13.15, the equilibrium would be:

Scenario 13.6 Consider the following game. Payoffs are in millions of dollars. -In the game in Scenario 13.6,

You are playing a game in which a dollar bill is auctioned. The highest bidder receives the dollar in return for the amount bid. However, the second-highest bidder must pay the amount that he or she bids, and gets nothing in return. The optimal strategy is:

Scenario 13.2 Consider the following game: -In the game in Scenario 13.2, the equilibrium strategies:

Consider the following game in which two firms decide how much of a homogeneous good to produce. The annual profit payoffs for each firm are stated in the cell of the game matrix, and Firm A's payoffs appear first in the payoff pairs: What are the dominant strategies in this game?

A "sequential game" is:

Which of the following situations is likely to generate noncooperative behavior in repeated games?

Scenario 13.10 Consider the game below: -The game in Scenario 13.10 is:

Relative to a simultaneous-move situation, the gain to firm R from being able to move first in the game in Scenario 13.14, would be:

Preliminaries

The Basics of Supply and Demand

Consumer Behavior

Individual and Market Demand

Uncertainty and Consumer Behavior

Production

The Cost of Production

Profit Maximization and Competitive Supply

The Analysis of Competitive Markets

Market Power: Monopoly and Monopsony

Pricing With Market Power

Monopolistic Competition and Oligopoly

Markets for Factor Inputs

Investment, Time, and Capital Markets

General Equilibrium and Economic Efficiency

Markets With Asymmetric Information

Externalities and Public Goods

Behavioral Economics

Filters

Exam 13: Game Theory and Competitive Strategy

What is true about threats in the game in Scenario 13.15?

In the game in Scenario 13.10, there is:

Consider the Matching Pennies game: Suppose Player A always uses a pure strategy that selects heads. What is Player B's optimal response to this pure strategy?

Why does cooperative behavior break down in games with finite endpoints?

Scenario 13.3 Consider the following game: -In the game in Scenario 13.3, the equilibrium outcome:

In the game in Scenario 13.11, equilibrium is:

If Boring were able to move first in a sequential version of the game in Scenario 13.15, the equilibrium would be:

Scenario 13.6 Consider the following game. Payoffs are in millions of dollars. -In the game in Scenario 13.6,

You are playing a game in which a dollar bill is auctioned. The highest bidder receives the dollar in return for the amount bid. However, the second-highest bidder must pay the amount that he or she bids, and gets nothing in return. The optimal strategy is:

Scenario 13.2 Consider the following game: -In the game in Scenario 13.2, the equilibrium strategies:

Consider the following game in which two firms decide how much of a homogeneous good to produce. The annual profit payoffs for each firm are stated in the cell of the game matrix, and Firm A's payoffs appear first in the payoff pairs: What are the dominant strategies in this game?

A "sequential game" is:

Which of the following situations is likely to generate noncooperative behavior in repeated games?

Scenario 13.10 Consider the game below: -The game in Scenario 13.10 is:

Relative to a simultaneous-move situation, the gain to firm R from being able to move first in the game in Scenario 13.14, would be:

Preliminaries

The Basics of Supply and Demand

Consumer Behavior

Individual and Market Demand

Uncertainty and Consumer Behavior

Production

The Cost of Production

Profit Maximization and Competitive Supply

The Analysis of Competitive Markets

Market Power: Monopoly and Monopsony

Pricing With Market Power

Monopolistic Competition and Oligopoly

Markets for Factor Inputs

Investment, Time, and Capital Markets

General Equilibrium and Economic Efficiency

Markets With Asymmetric Information

Externalities and Public Goods

Behavioral Economics

Filters