Exam 7: The Cost of Production
Exam 1: Preliminaries78 Questions
Exam 2: The Basics of Supply and Demand139 Questions
Exam 3: Consumer Behavior134 Questions
Exam 4: Individual and Market Demand131 Questions
Exam 5: Uncertainty and Consumer Behavior150 Questions
Exam 6: Production125 Questions
Exam 7: The Cost of Production178 Questions
Exam 8: Profit Maximization and Competitive Supply164 Questions
Exam 9: The Analysis of Competitive Markets183 Questions
Exam 10: Market Power: Monopoly and Monopsony158 Questions
Exam 11: Pricing With Market Power130 Questions
Exam 12: Monopolistic Competition and Oligopoly120 Questions
Exam 13: Game Theory and Competitive Strategy150 Questions
Exam 14: Markets for Factor Inputs134 Questions
Exam 15: Investment, Time, and Capital Markets153 Questions
Exam 16: General Equilibrium and Economic Efficiency126 Questions
Exam 17: Markets With Asymmetric Information133 Questions
Exam 18: Externalities and Public Goods131 Questions
Exam 19: Behavioral Economics101 Questions
Select questions type
A variable cost function of the form: 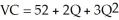 implies a marginal cost curve that is:
implies a marginal cost curve that is:
Free
(Multiple Choice)
4.9/5  (32)
(32)
Correct Answer:
B
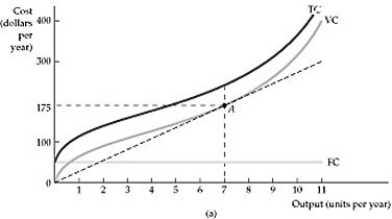 Figure 7.2.1
-Refer to Figure 7.2.1 above. When 7 units of output are produced:
Figure 7.2.1
-Refer to Figure 7.2.1 above. When 7 units of output are produced:
Free
(Multiple Choice)
4.7/5  (30)
(30)
Correct Answer:
C
Ronald's Outboard Motor Manufacturing plant has the following short-run cost function: 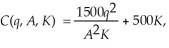 where q is the number of motors produced, K is the number of machines leased, and A is a productivity factor of technology. Currently, A is 25 and Ronald uses 20 machines. Ronald is investigating a new production technique. If he adopts the new technique, the productivity factor will become 36. If Ronald adopts the new technique, what is his average total cost of manufacturing 140 motors? Did the increase in the productivity factor increase or decrease the average total cost of producing 140 motors?
where q is the number of motors produced, K is the number of machines leased, and A is a productivity factor of technology. Currently, A is 25 and Ronald uses 20 machines. Ronald is investigating a new production technique. If he adopts the new technique, the productivity factor will become 36. If Ronald adopts the new technique, what is his average total cost of manufacturing 140 motors? Did the increase in the productivity factor increase or decrease the average total cost of producing 140 motors?
Free
(Essay)
4.9/5  (37)
(37)
Correct Answer:
Initially, Ronald's average total cost of producing 140 motors is:  With the new technique, Ronald's average total cost of producing 140 motors is:
With the new technique, Ronald's average total cost of producing 140 motors is: 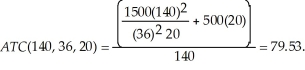 The increase in the productivity factor associated with the new technique decreases the average total cost of producing 140 units by $8.70 per unit.
The increase in the productivity factor associated with the new technique decreases the average total cost of producing 140 units by $8.70 per unit.
Trisha believes the production of a dress requires 4 labor hours and 2 machine hours to produce. If Trisha decides to operate in the short run, she must spend $500 to lease her business space. Also, a labor hour costs $15 and a machine hour costs $35. What is Trisha's cost of production as a function of dresses produced?
(Essay)
4.9/5  (37)
(37)
Consider the following statements when answering this question: I. A firm's marginal cost curve does not depend on the level of fixed costs.
II) As output increases the difference between a firm's average total cost and average variable cost curves cannot rise.
(Multiple Choice)
4.8/5  (39)
(39)
Cogswell Cogs can jointly produce cogs or rotors. The joint cost function is: 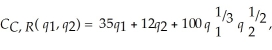 where q1 is the number of cogs and q2 is the number of rotors Cogswell produces. If Cogswell produces cogs alone, the cost function is:
where q1 is the number of cogs and q2 is the number of rotors Cogswell produces. If Cogswell produces cogs alone, the cost function is: 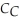 (
( 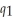 ) = 35
) = 35 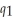 . If Cogswell produces rotors alone, the cost function is:
. If Cogswell produces rotors alone, the cost function is: 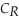 (
( 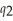 ) = 12
) = 12 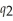 . Calculate Cogswell's degree of economies of scope if he produces 64 cogs and 16 rotors.
. Calculate Cogswell's degree of economies of scope if he produces 64 cogs and 16 rotors.
(Essay)
4.7/5  (36)
(36)
The total cost (TC) of producing computer software diskettes (Q) is given as: 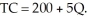 What is the fixed cost?
What is the fixed cost?
(Multiple Choice)
4.8/5  (32)
(32)
In a short-run production process, the marginal cost is rising and the average variable cost is falling as output is increased. Thus,
(Multiple Choice)
4.9/5  (43)
(43)
Bridget's Brewery can jointly produce dry stout and sweet stout. The cost function for joint production is: 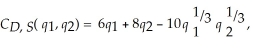 where
where 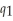 is the quantity of dry stout and
is the quantity of dry stout and 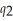 is the quantity of sweet stout that Bridget produces. If the brewery produces dry stout alone, the firm's cost function is:
is the quantity of sweet stout that Bridget produces. If the brewery produces dry stout alone, the firm's cost function is: 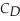 (
( 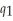 ) = 6
) = 6 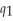 . If the brewery produces sweet stout alone, the cost function is:
. If the brewery produces sweet stout alone, the cost function is: 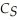 (
( 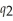 ) = 8
) = 8 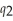 . Calculate Bridget's degree of economies of scope if she produces 27 units of dry stout and 64 units of sweet stout.
. Calculate Bridget's degree of economies of scope if she produces 27 units of dry stout and 64 units of sweet stout.
(Essay)
4.9/5  (34)
(34)
In order for a taxicab to be operated in New York City, it must have a medallion on its hood. Medallions are expensive, but can be resold, and are therefore an example of:
(Multiple Choice)
4.9/5  (46)
(46)
If two different fuel sources (e.g., coal and natural gas) are perfect substitutes in the long-run production of energy. How will a profit maximizing firm choose between these two inputs?
(Multiple Choice)
4.8/5  (38)
(38)
Suppose capital and labor are perfect substitutes in a long-run production process. If labor costs $15 per hour and the rental rate of capital is $20 per hour, what can we say about the profit maximizing choice of labor and capital inputs?
(Multiple Choice)
4.9/5  (34)
(34)
Which of the following costs are always increasing as output increases?
(Multiple Choice)
4.9/5  (33)
(33)
To model the input decisions for a production system, we plot labor on the horizontal axis and capital on the vertical axis. In the short run, labor is a variable input and capital is fixed. The short-run expansion path for this production system is:
(Multiple Choice)
4.9/5  (37)
(37)
Your firm owns an old truck that is used to make local deliveries. The truck is fully depreciated and only costs $1.20 per hour to operate, but you could rent it to another firm for $15.00 per hour. What is the opportunity cost of operating this truck in your business?
(Multiple Choice)
4.7/5  (29)
(29)
One Guy's Pizza jointly produces pizzas and calzones. The joint cost function is: 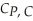 (
( 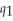 ,
, 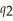 ) = 4
) = 4 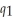 + 0.8
+ 0.8 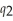 - 1.5
- 1.5 
 , where
, where 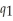 is the number of pizzas and
is the number of pizzas and 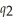 is the number of calzones One Guy's Pizza produces. If One Guy produces pizzas alone, the cost function is:
is the number of calzones One Guy's Pizza produces. If One Guy produces pizzas alone, the cost function is: 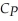 (
( 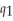 ) = 4
) = 4 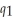 . If One Guy produces calzones alone, the cost function is:
. If One Guy produces calzones alone, the cost function is: 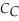 (
( 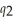 ) = 0.8
) = 0.8 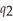 . Calculate One Guy's degree of economies of scope if they produce 1,024 pizzas and 243 calzones.
. Calculate One Guy's degree of economies of scope if they produce 1,024 pizzas and 243 calzones.
(Essay)
4.8/5  (33)
(33)
Consider the following statements when answering this question: I. If the marginal product of labor falls whenever more labor is used, and labor is the only factor of production used by the firm, than at every output level the firm's short-run average variable cost exceeds marginal cost.
II) If labor obeys the law of diminishing returns, and is the only factor of production used by the firm, then at every output level short-run average variable costs exceed marginal costs.
(Multiple Choice)
4.9/5  (31)
(31)
A paper company dumps nondegradable waste into a river that flows by the firm's plant. The firm estimates its production function to be:
Q = 6KW,
where Q = annual paper production measured in pounds, 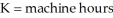 of capital, and
of capital, and 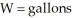 of polluted water dumped into the river per year. The marginal products of capital and labor are given as follows:
MPK = 6W MPW = 6K
The firm currently faces no environmental regulation in dumping waste into the river. Without regulation, it costs the firm $7.50 per gallon dumped. The firm estimates a $30 per hour rental rate on capital. The operating budget for capital and waste water is $300,000 per year.
a. Determine the firm's optimal ratio of waste water to capital.
b. Given the firm's $300,000 budget, how much capital and waste water should the firm employ? How much output will the firm produce?
c. The state environmental protection agency plans to impose a $7.50 effluent fee for each gallon that is dumped. Assuming that the firm intends to maintain its pre-fee output, how much capital and waste water should the firm employ? How much will the firm pay in effluent fees? What happens to the firm's cost as a result of the effluent fee?
of polluted water dumped into the river per year. The marginal products of capital and labor are given as follows:
MPK = 6W MPW = 6K
The firm currently faces no environmental regulation in dumping waste into the river. Without regulation, it costs the firm $7.50 per gallon dumped. The firm estimates a $30 per hour rental rate on capital. The operating budget for capital and waste water is $300,000 per year.
a. Determine the firm's optimal ratio of waste water to capital.
b. Given the firm's $300,000 budget, how much capital and waste water should the firm employ? How much output will the firm produce?
c. The state environmental protection agency plans to impose a $7.50 effluent fee for each gallon that is dumped. Assuming that the firm intends to maintain its pre-fee output, how much capital and waste water should the firm employ? How much will the firm pay in effluent fees? What happens to the firm's cost as a result of the effluent fee?
(Essay)
4.8/5  (30)
(30)
In a short-run production process, the marginal cost is rising and the average total cost is falling as output is increased. Thus, marginal cost is:
(Multiple Choice)
5.0/5  (37)
(37)
Showing 1 - 20 of 178
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)