Exam 13: Game Theory and Competitive Strategy

Consider the following game that represents the payoffs from different advertising campaigns (low, medium, and high spending) for two political candidates that are running for a particular office. The values in the payoff matrix represent the share of the popular vote earned by each candidate: Under the version of the game with simultaneous moves, what is the Nash equilibrium?

Which of the below outcomes is the result of a Nash equilibrium in pure strategies for the game in Scenario 13.10?

To deter a potential entrant, an existing firm in a market may threaten to sharply increase production so that the entrant will be left with a small share of the market. The firm can make this threat credible by limiting its own options, and possible actions of this type include:

Scenario 13.16 Consider the pricing game below: -What is true about dominant strategies in the game in Scenario 13.16?

Refer to Scenario 13.1. If your negotiated price had been $350 instead of $250, the sum of consumer surplus and producer surplus would be:

Scenario 13.12 Consider the game below: -If the Battle of the Sexes game were played sequentially,

Casey's General Store is considering placing a store in Hamilton, Missouri. If they place the store in Hamilton and no other convenience store enters the Hamilton market, they'll earn profits of $100,000 per year. If competitors do enter, Casey's profits as well as the competitors' profits will be reduced to $0 per year. If a competitor enters the Hamilton market and Casey's does not, the competitor's profits will be $100,000 per year. 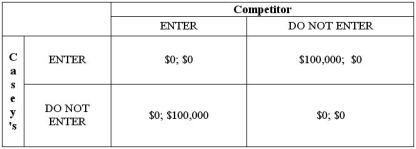Does either player have a dominant strategy? Does the game have any Nash equilibria? What is the maximin strategy of each player in the game?

Scenario 13.1 You are negotiating with your florist over the price of flowers for your wedding. You value the floral arrangements at $500. The florist's cost for the arrangement is $200. You finally settled on a price of $250. -Refer to Scenario 13.1. Your negotiations are an example of:

Consider the Battle of the Sexes game: Suppose both players use mixed strategies for this game. Jim chooses wrestling with probability 0.9, and Joan chooses wrestling with probability 0.5. What are the expected payoffs for the players?

Consider the Matching Pennies game: Suppose Player B always uses a mixed strategy with probability of 3/4 for head and 1/4 for tails. Which of the following strategies for Player A provides the highest expected payoff?