Exam 22: Linear Programming: The Simplex Method
Exam 1: Introduction to Quantitative Analysis96 Questions
Exam 2: Probability Concepts and Applications155 Questions
Exam 3: Decision Analysis128 Questions
Exam 4: Regression Models129 Questions
Exam 5: Forecasting138 Questions
Exam 6: Inventory Control Models147 Questions
Exam 7: Linear Programming Models: Graphical and Computer Methods141 Questions
Exam 8: Linear Programming Applications89 Questions
Exam 9: Transportation, Assignment, and Network Models112 Questions
Exam 10: Integer Programming, Goal Programming, and Nonlinear Programming86 Questions
Exam 11: Project Management142 Questions
Exam 12: Waiting Lines and Queuing Theory Models127 Questions
Exam 13: Simulation Modeling94 Questions
Exam 14: Markov Analysis103 Questions
Exam 15: Statistical Quality Control96 Questions
Exam 16: Analytic Hierarchy Process66 Questions
Exam 17: Dynamic Programming86 Questions
Exam 18: Decision Theory and the Normal Distribution62 Questions
Exam 19: Game Theory59 Questions
Exam 20: Mathematical Tools: Determinants and Matrices104 Questions
Exam 21: Calculus-Based Optimization39 Questions
Exam 22: Linear Programming: The Simplex Method98 Questions
Exam 23: Transportation, Assignment, and Network Algorithms120 Questions
Select questions type
In a maximization problem, the Cj - Zj row gives the net loss from introducing one unit of each variable into the solution.
(True/False)
4.8/5  (30)
(30)
Using the simplex method, we know we have an optimal solution when
(Multiple Choice)
4.9/5  (49)
(49)
In 1984, who developed an alternative to the simplex algorithm, which often takes significantly less computer time to solve very large-scale LP problems?
(Multiple Choice)
4.8/5  (38)
(38)
Artificial variables can be used in both maximization and minimization problems but are most often used in minimization problems.
(True/False)
4.8/5  (36)
(36)
A simplex formulation that suffers from degeneracy means that the problem has no optimal solution.
(True/False)
4.7/5  (32)
(32)
In the simplex process, the new pivot row is found by dividing each number in the row by the pivot number.
(True/False)
4.8/5  (32)
(32)
If, in the final optimal simplex tableau, the Cj - Zj value for a nonbasic variable is zero, this implies
(Multiple Choice)
4.9/5  (31)
(31)
Because slack variables yield no profit, they are not included in the objective function when creating the initial simplex tableau.
(True/False)
4.8/5  (41)
(41)
The substitution rates in the slack variable column can be used to determine the actual values of the solution mix variables if the right-hand side of a constraint is changed.What is the relationship that is used to find those values?
(Essay)
4.9/5  (34)
(34)
If, in the optimal tableau of a linear programming problem, an artificial variable is present in the solution mix, this implies
(Multiple Choice)
4.8/5  (32)
(32)
Table M7-3 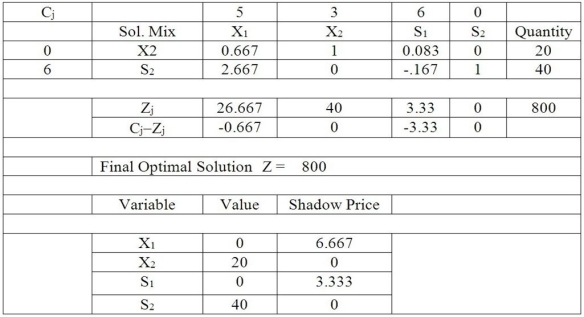 -According to Table M7-3, which is the final simplex tableau for a problem with two variables and two constraints, what can be said about the optimal solution and the constraints?
-According to Table M7-3, which is the final simplex tableau for a problem with two variables and two constraints, what can be said about the optimal solution and the constraints?
(Multiple Choice)
4.9/5  (31)
(31)
Upon retirement, Mr.Klaws started to make two types of children's wooden toys in his shop.Wuns yield a variable profit of $8 each, and Toos have a contribution margin of $9 each.Even though his electric saw overheats, he can make 7 Wuns or 14 Toos each day.Since he doesn't have equipment for drying the lacquer finish he puts on the toys, the drying operation limits him to 16 Wuns or 8 Toos per day.The final tableau for Mr.Klaws' problem would be: 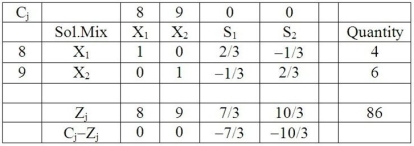 (a)What would the value be of an additional unit of constraint #1?
(b)What would the value be of an additional unit of constraint #2?
(a)What would the value be of an additional unit of constraint #1?
(b)What would the value be of an additional unit of constraint #2?
(Short Answer)
4.9/5  (31)
(31)
For a maximization problem, the Zj values in the body of the simplex table represent the gross profit given up by adding one unit of this variable into the current solution.
(True/False)
4.8/5  (36)
(36)
How does Karmarkar's Algorithm differ from the simplex method?
(Multiple Choice)
4.9/5  (35)
(35)
Write the dual of the following linear program.
Maximize 3 X1 + 5X2
Subject to: 4 X1 + 2 X2 ≤ 44
X1 + 2 X2 ≤ 24
X1, X2 ≥ 0
(Essay)
4.9/5  (51)
(51)
A primal linear programming problem has four variables and three constraints.The dual of this will have
(Multiple Choice)
4.8/5  (41)
(41)
A solved LP problem indicated that the optimal solution was X1 = 5, X2 = 10, A1 = 40.The first constraint was: 4X1 + 2X2 ≥ 80.This solution is
(Multiple Choice)
4.9/5  (28)
(28)
Table M7-3  -According to Table M7-3, which is the final simplex tableau for a problem with two variables and two constraints, the 0.667 in the X1 column means that
-According to Table M7-3, which is the final simplex tableau for a problem with two variables and two constraints, the 0.667 in the X1 column means that
(Multiple Choice)
5.0/5  (38)
(38)
Showing 61 - 80 of 98
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)