Exam 22: Linear Programming: The Simplex Method
Exam 1: Introduction to Quantitative Analysis96 Questions
Exam 2: Probability Concepts and Applications155 Questions
Exam 3: Decision Analysis128 Questions
Exam 4: Regression Models129 Questions
Exam 5: Forecasting138 Questions
Exam 6: Inventory Control Models147 Questions
Exam 7: Linear Programming Models: Graphical and Computer Methods141 Questions
Exam 8: Linear Programming Applications89 Questions
Exam 9: Transportation, Assignment, and Network Models112 Questions
Exam 10: Integer Programming, Goal Programming, and Nonlinear Programming86 Questions
Exam 11: Project Management142 Questions
Exam 12: Waiting Lines and Queuing Theory Models127 Questions
Exam 13: Simulation Modeling94 Questions
Exam 14: Markov Analysis103 Questions
Exam 15: Statistical Quality Control96 Questions
Exam 16: Analytic Hierarchy Process66 Questions
Exam 17: Dynamic Programming86 Questions
Exam 18: Decision Theory and the Normal Distribution62 Questions
Exam 19: Game Theory59 Questions
Exam 20: Mathematical Tools: Determinants and Matrices104 Questions
Exam 21: Calculus-Based Optimization39 Questions
Exam 22: Linear Programming: The Simplex Method98 Questions
Exam 23: Transportation, Assignment, and Network Algorithms120 Questions
Select questions type
An infeasible solution is indicated when all the Cj - Zj row entries are of the proper sign to imply optimality, but an artificial variable remains in the solution.
(True/False)
4.9/5  (31)
(31)
In LP problems with more than two variables, the area of feasible solutions is known as an n-dimensional
(Multiple Choice)
4.8/5  (32)
(32)
The constraint 5X1 + 6X2 ≥ 30, when converted to an = constraint for use in the simplex algorithm, will be 5 X1 + 6 X2 - S = 30.
(True/False)
4.9/5  (45)
(45)
In applying the simplex solution procedure to a minimization problem to determine which variable enters the solution mix
(Multiple Choice)
4.8/5  (35)
(35)
Table M7-3 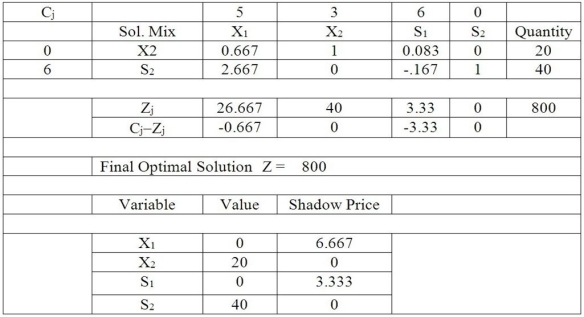 -According to Table M7-3, which is the final simplex tableau for a problem with two variables and two constraints, what is the maximum possible profit (objective function value)for this problem?
-According to Table M7-3, which is the final simplex tableau for a problem with two variables and two constraints, what is the maximum possible profit (objective function value)for this problem?
(Multiple Choice)
5.0/5  (32)
(32)
A minimization problem with two decision variables and three ≥ constraints can have two non-basic surplus variables.
(True/False)
4.8/5  (38)
(38)
The simplex method begins with an initial feasible solution in which all real variables are set equal to 0.
(True/False)
4.7/5  (32)
(32)
In a maximization problem, if a variable is to enter the solution, it must have a positive coefficient in the Cj - Zj row.
(True/False)
4.9/5  (33)
(33)
Shadow prices are the positives of the numbers in the Cj - Zj row's slack variable columns.
(True/False)
4.7/5  (36)
(36)
Convert the following linear program into a simplex model form.
Maximize 8X + 10Y
Subject to: 5X + 3Y ≤ 34
2X + 3Y = 22
X ≥ 3
X, Y ≥ 0
(Essay)
4.7/5  (35)
(35)
Table M7-3  -According to Table M7-3, which is the final simplex tableau for a linear programming problem (maximization), what would happen to profits if the X1 column were selected as the pivot column and another iteration of the simplex algorithm were performed?
-According to Table M7-3, which is the final simplex tableau for a linear programming problem (maximization), what would happen to profits if the X1 column were selected as the pivot column and another iteration of the simplex algorithm were performed?
(Multiple Choice)
4.9/5  (34)
(34)
Consider the following linear programming problem: Maximize 40 X1 + 30 X2 + 60X3
Subject to: X1 + X2 + X3 ≥ 90
12 X1 + 8 X2 + 10 X3 ≤ 1500
X1 = 20
X3 ≤ 100
X1 , X2 , X3 ≥ 0
How many slack, surplus, and artificial variables would be necessary if the simplex algorithm were used to solve this problem?
(Multiple Choice)
4.9/5  (45)
(45)
Table M7-1 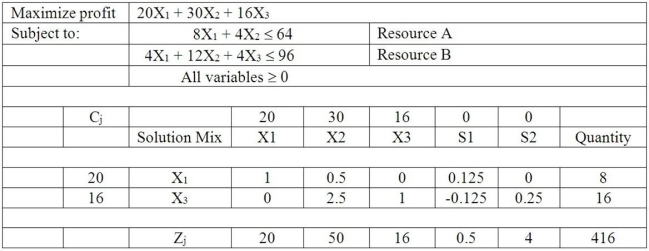 -According to Table M7-1, it is currently profitable to produce some units of X1 and the current profit per unit of X1 is $20.What is the lowest value that this could be to allow this variable to remain in the basis?
-According to Table M7-1, it is currently profitable to produce some units of X1 and the current profit per unit of X1 is $20.What is the lowest value that this could be to allow this variable to remain in the basis?
(Multiple Choice)
4.9/5  (40)
(40)
The number -2 in the X2 column and X1 row of a simplex tableau implies that
(Multiple Choice)
4.8/5  (38)
(38)
In a maximization problem, if a variable is to enter the solution, it must have a negative coefficient in the Cj - Zj row.
(True/False)
4.8/5  (28)
(28)
Karmarkar's algorithm reaches a solution quickly by compressing the edges of the feasible region.
(True/False)
4.8/5  (41)
(41)
The dual problem formulation can be solved using the same simplex process used for the primal formulation.
(True/False)
4.8/5  (29)
(29)
Showing 81 - 98 of 98
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)