Exam 17: Dynamic Programming
Exam 1: Introduction to Quantitative Analysis96 Questions
Exam 2: Probability Concepts and Applications155 Questions
Exam 3: Decision Analysis128 Questions
Exam 4: Regression Models129 Questions
Exam 5: Forecasting138 Questions
Exam 6: Inventory Control Models147 Questions
Exam 7: Linear Programming Models: Graphical and Computer Methods141 Questions
Exam 8: Linear Programming Applications89 Questions
Exam 9: Transportation, Assignment, and Network Models112 Questions
Exam 10: Integer Programming, Goal Programming, and Nonlinear Programming86 Questions
Exam 11: Project Management142 Questions
Exam 12: Waiting Lines and Queuing Theory Models127 Questions
Exam 13: Simulation Modeling94 Questions
Exam 14: Markov Analysis103 Questions
Exam 15: Statistical Quality Control96 Questions
Exam 16: Analytic Hierarchy Process66 Questions
Exam 17: Dynamic Programming86 Questions
Exam 18: Decision Theory and the Normal Distribution62 Questions
Exam 19: Game Theory59 Questions
Exam 20: Mathematical Tools: Determinants and Matrices104 Questions
Exam 21: Calculus-Based Optimization39 Questions
Exam 22: Linear Programming: The Simplex Method98 Questions
Exam 23: Transportation, Assignment, and Network Algorithms120 Questions
Select questions type
GATRA, the Greater Attleboro-Taunton Regional Transit Authority, serves six cities (City 1-City 6). While there are many restrictions (primarily roads on which they may not travel), they do have some choice of routes. The distances between cities, along permitted routes, are presented below.
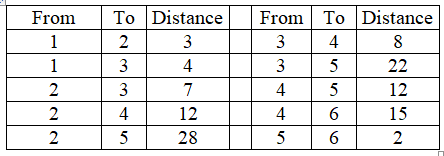 -What is the minimum distance that must be traveled to get from City 1 to City 6?
-What is the minimum distance that must be traveled to get from City 1 to City 6?
(Multiple Choice)
4.7/5  (27)
(27)
Your local paper carrier could make use of the shortest-route technique.
(True/False)
4.8/5  (34)
(34)
GATRA, the Greater Attleboro-Taunton Regional Transit Authority, serves six cities (City 1-City 6). While there are many restrictions (primarily roads on which they may not travel), they do have some choice of routes. The distances between cities, along permitted routes, are presented below.
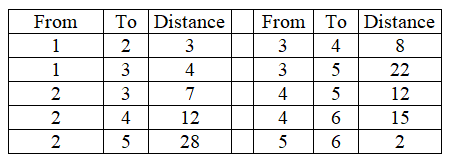 -What is the minimum distance that must be traveled to get from City 1 to City 6?
-What is the minimum distance that must be traveled to get from City 1 to City 6?
(Multiple Choice)
5.0/5  (33)
(33)
The arrow labeled S2 in Figure M2.1 represents the output from stage 1.
(True/False)
4.9/5  (42)
(42)
Alex returns from a weekend hiking with his son and discovers a note from his unstable wife on the kitchen counter.Alex decides to take the shortest possible route to the meanest lawyer in Bearington to put an end to this marriage.What is the minimum distance required to take Alex to his new lawyer whose office is at node 7?
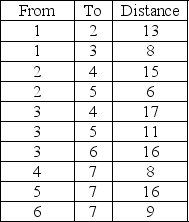
(Short Answer)
4.9/5  (31)
(31)
The formula sn = tn(sn-1,dn,rn)allows us to go from one stage to the next in Figure M2.1.
(True/False)
4.8/5  (27)
(27)
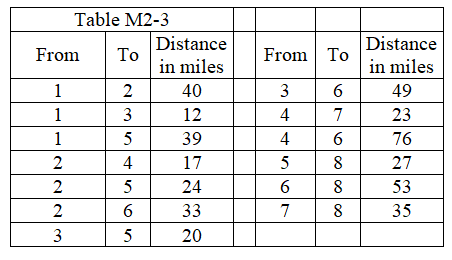 -The above information describes a shortest-route problem with the distance in miles.How many stages will this dynamic programming problem have?
-The above information describes a shortest-route problem with the distance in miles.How many stages will this dynamic programming problem have?
(Multiple Choice)
4.7/5  (36)
(36)
In dynamic programming, the decision rules defining an optimal policy give optimal decisions for any entering condition at any stage.
(True/False)
4.8/5  (37)
(37)
The following information describes a shortest-route problem with the distance in miles.Which nodes are involved in the shortest route? 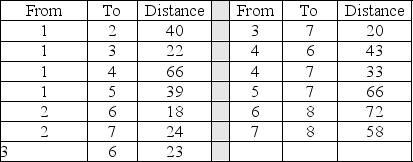
(Multiple Choice)
4.8/5  (33)
(33)
There are seven cities (City 1-City 7) served by Acme Trucking. Route availability is limited. The distances, in hundreds of miles, are given in the table below for each route.
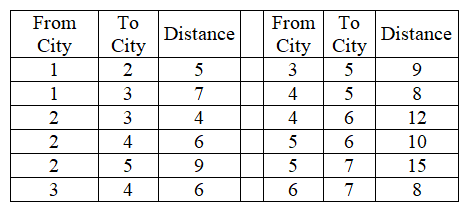 -If the truck were required to take the route from City 4 to City 5, what would be the shortest distance from City 1 to City 7?
-If the truck were required to take the route from City 4 to City 5, what would be the shortest distance from City 1 to City 7?
(Multiple Choice)
4.8/5  (38)
(38)
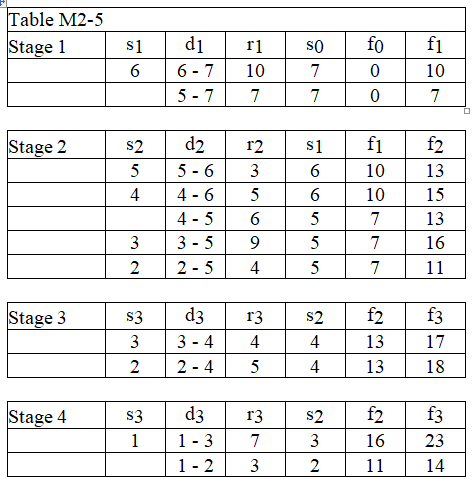 -Using the data in Table M2-5, determine the optimal distance of stage 3.
-Using the data in Table M2-5, determine the optimal distance of stage 3.
(Multiple Choice)
4.7/5  (39)
(39)
GATRA, the Greater Attleboro-Taunton Regional Transit Authority, serves six cities (City 1-City 6). While there are many restrictions (primarily roads on which they may not travel), they do have some choice of routes. The distances between cities, along permitted routes, are presented below.
 -What is the shortest route?
-What is the shortest route?
(Multiple Choice)
4.8/5  (32)
(32)
The second step in solving a dynamic programming problem is to solve the last stage of the problem for all conditions or states.
(True/False)
4.9/5  (37)
(37)
There are seven cities (City 1-City 7) served by Acme Trucking. Route availability is limited. The distances, in hundreds of miles, are given in the table below for each route.
 -If the truck were required to take the route from City 4 to City 5, what would be the overall route?
-If the truck were required to take the route from City 4 to City 5, what would be the overall route?
(Multiple Choice)
5.0/5  (27)
(27)
There are seven cities (City 1-City 7) served by Acme Trucking. Route availability is limited. The distances, in hundreds of miles, are given in the table below for each route.
 -What route should the truck from City 1 to City 7 take?
-What route should the truck from City 1 to City 7 take?
(Multiple Choice)
4.8/5  (38)
(38)
 -Using the data in Table M2-5, determine the optimal arc of stage 2.
-Using the data in Table M2-5, determine the optimal arc of stage 2.
(Multiple Choice)
4.9/5  (36)
(36)
Showing 41 - 60 of 86
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)