Exam 17: Dynamic Programming
Exam 1: Introduction to Quantitative Analysis96 Questions
Exam 2: Probability Concepts and Applications155 Questions
Exam 3: Decision Analysis128 Questions
Exam 4: Regression Models129 Questions
Exam 5: Forecasting138 Questions
Exam 6: Inventory Control Models147 Questions
Exam 7: Linear Programming Models: Graphical and Computer Methods141 Questions
Exam 8: Linear Programming Applications89 Questions
Exam 9: Transportation, Assignment, and Network Models112 Questions
Exam 10: Integer Programming, Goal Programming, and Nonlinear Programming86 Questions
Exam 11: Project Management142 Questions
Exam 12: Waiting Lines and Queuing Theory Models127 Questions
Exam 13: Simulation Modeling94 Questions
Exam 14: Markov Analysis103 Questions
Exam 15: Statistical Quality Control96 Questions
Exam 16: Analytic Hierarchy Process66 Questions
Exam 17: Dynamic Programming86 Questions
Exam 18: Decision Theory and the Normal Distribution62 Questions
Exam 19: Game Theory59 Questions
Exam 20: Mathematical Tools: Determinants and Matrices104 Questions
Exam 21: Calculus-Based Optimization39 Questions
Exam 22: Linear Programming: The Simplex Method98 Questions
Exam 23: Transportation, Assignment, and Network Algorithms120 Questions
Select questions type
The data below is a dynamic programming solution for a shortest route problem.
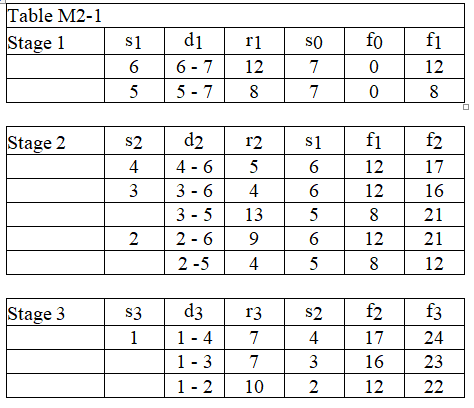 -Using the data in Table M2-1, determine the distance of stage 2 for the optimal route.
-Using the data in Table M2-1, determine the distance of stage 2 for the optimal route.
(Multiple Choice)
5.0/5  (34)
(34)
The data below is a dynamic programming solution for a shortest route problem.
 -Using the data in Table M2-1, what is the optimal arc of stage 3?
-Using the data in Table M2-1, what is the optimal arc of stage 3?
(Multiple Choice)
4.8/5  (36)
(36)
Identify two types of problems that can be solved by dynamic programming.
(Short Answer)
4.7/5  (32)
(32)
In Figure M2.1 there is a function t2 that is not depicted, that converts s2 and d2 to s1.
(True/False)
4.8/5  (39)
(39)
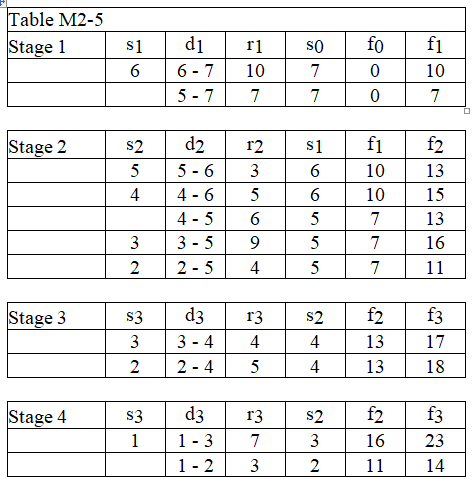 -Using the data in Table M2-5, determine the optimal distance of stage 2.
-Using the data in Table M2-5, determine the optimal distance of stage 2.
(Multiple Choice)
4.8/5  (31)
(31)
In dynamic programming, there is a state variable defined for every stage.
(True/False)
4.9/5  (38)
(38)
GATRA, the Greater Attleboro-Taunton Regional Transit Authority, serves six cities (City 1-City 6). While there are many restrictions (primarily roads on which they may not travel), they do have some choice of routes. The distances between cities, along permitted routes, are presented below.
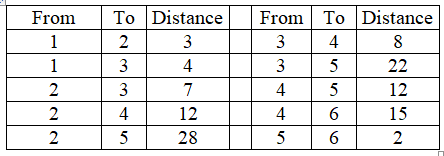 -Which routes should be traveled?
-Which routes should be traveled?
(Multiple Choice)
4.8/5  (38)
(38)
Both dynamic programming and linear programming take a multi-stage approach to solving problems.
(True/False)
4.8/5  (23)
(23)
The problem that NASA has in determining what types of cargo may be loaded on the space shuttle is an example of a knapsack problem.
(True/False)
4.9/5  (38)
(38)
The data below is a dynamic programming solution for a shortest route problem.
 -Using the data in Table M2-1, determine the distance of stage 3 for the optimal route.
-Using the data in Table M2-1, determine the distance of stage 3 for the optimal route.
(Multiple Choice)
4.9/5  (38)
(38)
The data below is a dynamic programming solution for a shortest route problem.
 -Using the data in Table M2-1, determine the distance of stage 1 for the optimal route.
-Using the data in Table M2-1, determine the distance of stage 1 for the optimal route.
(Multiple Choice)
4.8/5  (35)
(35)
 -Using the data in Table M2-5, determine the optimal travel path from point 1 to point 7.
-Using the data in Table M2-5, determine the optimal travel path from point 1 to point 7.
(Multiple Choice)
4.8/5  (35)
(35)
For the bus line problem above, what is the minimum possible distance to travel from City 1 to City 6?
(Multiple Choice)
4.7/5  (28)
(28)
There are three items (A, B, and C) that are to be shipped by air. The weights of these are 4, 5, and 3 tons, respectively, and the plane can carry 13 tons. The profits (in thousands of dollars) generated by these are 3 for A, 4 for B, and 2 for C. There are four units of each available for shipment. If this were to be solved as a dynamic programming problem, how many stages would there be?
(Multiple Choice)
4.7/5  (40)
(40)
Showing 21 - 40 of 86
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)