Exam 10: Integer Programming, Goal Programming, and Nonlinear Programming

Another name for a 0-1 variable is a(n)________ variable.

Assignment problems solved previously by linear programming techniques are also examples of

The concept of a local optimum is affiliated with which of the following?

A goal programming problem had two goals (with no priorities assigned).Goal number 1 was to achieve a cost of $2,400 and goal number 2 was to have no idle time for workers in the factory.The optimal solution to this problem resulted in a cost of $2,400 and no idle time.What was the value for the objective function for this goal programming problem?

What is the optimal solution to the problem described in Table 10-6?

We do not have a general method for solving all types of ________ problems.

The overall best solution in a nonlinear program is a

An integer programming solution can never produce a greater profit objective than the LP solution to the same problem.

Data Equipment Inc.produces two models of a retail price scanner, a sophisticated model that can be networked to a central processing unit and a stand-alone model for small retailers.The major limitations of the manufacturing of these two products are labor and material capacities.The following table summarizes the usages and capacities associated with each product. Capacity 800 hr/day 1,500 comp/day The typical LP formulation for this problem is: Maximize P = $160 X1 + $95 X2 Subject to: 8 X1 + 5 X2 ≤ 800 20 X1 + 7 X2 ≤ 1500 X1, X2 ≥ 0 However, the management of DEI has prioritized several goals that are to be attained by manufacturing: Management had decided to severely limit overtime. Management has established a profit goal of $15,000 per day. Due to the difficulty of obtaining components from non-routine suppliers, management wants to end production with at least 50 units of each component remaining in stock. Management also believes that they should produce at least 30 units of the network model. Given the above additional information, set this up as a goal programming problem.

The concept of "satisficing" is affiliated with which of the following?

Consider the following 0-1 integer programming problem: Minimize 20X + 36Y + 24Z Subject to: 2X + 4Y + 3Z ≥ 7 12X + 8Y + 10Z ≥ 25 X, Y, Z must be 0 or 1 If we wish to add the constraint that X must be positive, and that only Y or Z, but not both, can be positive, how would the additional constraint(s)be written?

Unfortunately, multiple goals in goal programming are not able to be prioritized and solved.

A haberdashery produces scarves, ascots, and capes.The profit function for the haberdashery is expressed by the following equation: profit = 4S + 2A + 5C + 0.8S² + 1.4A² + 2C² + 2SAC.It takes 9 minutes to produce a scarf, 13 minutes to produce an ascot and 30 minutes to produce a cape.There is also a nonlinear element to the usage of time governed by the double the product of scarves, ascots and capes produced.There is a total of 50 hours available for labor each week.Shipping poses another issue for the haberdashery; packaging and loading trucks for online orders is time consuming and that function is handled by the haberdashery owner's mother who comes in after her afternoon walk around a local almost-deserted mall.It takes 1.5 minutes to pack and load a scarf, 2.5 minutes to pack and load an ascot, and 3.5 minutes to pack and load a cape.There is also a cross product term for packing and loading that is 0.15SA + 0.075SC + 0.025AC that must be considered.The haberdasher's mother is available only 30 hours a week, but the haberdasher is prepared to lay down the law and insist she stop this mall walking foolishness and devote herself completely to his business.For the time being, consider her time as only 30 hours.There must be at least 50 scarves, 100 ascots, and 25 capes produced each week.Formulate a nonlinear integer program representing the profit maximization problem for the haberdashery.

Smalltime Investments Inc.is going to purchase new computers for most of the employees.There are ten employees, and at least eight computers must be purchased.The cost of the basic personal computer with monitor and disk drive is $2,000, while the deluxe version with VGA and advanced processor is $3,500.Due to internal politics, the number of deluxe computers must be no more than half the number of regular computers, but at least three deluxe computers must be purchased.The budget is $27,000.Formulate this as an integer programming problem to maximize the number of computers purchased.

A haberdashery produces scarves, ascots, and capes.The profit function for the haberdashery is expressed by the following equation: profit = 4S + 2A + 5C + 0.8S² + 1.4A² + 2C^{2 + 2SAC}.It takes 10 minutes to produce a scarf, 15 minutes to produce an ascot and 30 minutes to produce a cape.There is a total of 50 hours available for labor each week.There must be at least 50 scarves, 100 ascots, and 25 capes produced each week.Formulate a nonlinear program representing the profit maximization problem for the haberdashery.

Allied Manufacturing has three factories located in Dallas, Houston, and New Orleans.They each produce the same product and ship to three regional warehouses: #1, #2, and #3.The cost of shipping one unit of each product to each of the three destinations is given below. 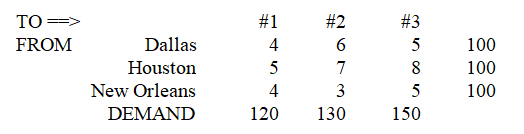There is no way to meet the demand for each warehouse.Therefore, the company has decided to set the following goals: (1)the number shipped from each source should be as close to 100 units as possible (overtime may be used if necessary), (2)the number shipped to each destination should be as close to the demand as possible, (3)the total cost should be close to $1,400.Formulate this as a goal programming problem.

Quadratic programming contains squared terms in the constraints.

Which of the following statements is false concerning goal programming?

A quadratic programming problem involves which of the following conditions?

A goal programming problem had two goals (with no priorities assigned).Goal number 1 was to achieve a profit of $2,400 and goal number 2 was to have no idle time for workers in the factory.The optimal solution to this problem resulted in a profit of $2,300 and no idle time.What was the value for the objective function for this goal programming problem?