Exam 15: Markov Analysis
Exam 1: Introduction to Quantitative Analysis63 Questions
Exam 2: Probability Concepts and Applications145 Questions
Exam 3: Decision Analysis119 Questions
Exam 4: Regression Models120 Questions
Exam 5: Forecasting101 Questions
Exam 6: Inventory Control Models113 Questions
Exam 7: Linear Programming Models: Graphical and Computer Methods100 Questions
Exam 8: Linear Programming Applications96 Questions
Exam 9: Transportation and Assignment Models80 Questions
Exam 10: Integer Programming, Goal Programming, and Nonlinear Programming88 Questions
Exam 11: Network Models86 Questions
Exam 12: Project Management123 Questions
Exam 13: Waiting Lines and Queuing Theory Models133 Questions
Exam 14: Simulation Modeling68 Questions
Exam 15: Markov Analysis78 Questions
Exam 16: Statistical Quality Control87 Questions
Select questions type
Markov analysis is a technique that deals with the probabilities of future occurrences by
(Multiple Choice)
4.9/5  (38)
(38)
Table 15-3
Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium. This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3). A transition matrix, indicating the probability that a resident in one city will travel to another, is given below. Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis.
C F T
Transition matrix: ![Table 15-3 Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium. This state contains three cities: Chaos (C<sub>1</sub>), Frenzy (C<sub>2</sub>), and Tremor (C<sub>3</sub>). A transition matrix, indicating the probability that a resident in one city will travel to another, is given below. Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis. C F T Transition matrix: π(0) = [100, 100, 100] -Using the data given in Table 15-3, how many seats should Cuthbert schedule for travel from Chaos to Tremor for tomorrow?](https://storage.examlex.com/TB2951/11eab9f8_75de_6ac3_b53a_65192602d25c_TB2951_11_TB2951_11_TB2951_11_TB2951_11.jpg)
![Table 15-3 Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium. This state contains three cities: Chaos (C<sub>1</sub>), Frenzy (C<sub>2</sub>), and Tremor (C<sub>3</sub>). A transition matrix, indicating the probability that a resident in one city will travel to another, is given below. Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis. C F T Transition matrix: π(0) = [100, 100, 100] -Using the data given in Table 15-3, how many seats should Cuthbert schedule for travel from Chaos to Tremor for tomorrow?](https://storage.examlex.com/TB2951/11eab9f8_75de_91d4_b53a_37f786bf4665_TB2951_11_TB2951_11_TB2951_11_TB2951_11.jpg) π(0) = [100, 100, 100]
-Using the data given in Table 15-3, how many seats should Cuthbert schedule for travel from Chaos to Tremor for tomorrow?
π(0) = [100, 100, 100]
-Using the data given in Table 15-3, how many seats should Cuthbert schedule for travel from Chaos to Tremor for tomorrow?
(Multiple Choice)
4.8/5  (43)
(43)
A certain firm has noticed that employees' salaries from year to year can be modeled by Markov analysis. The matrix of transition probabilities follows. 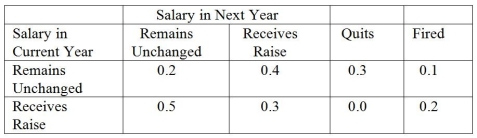 (a) Set up the matrix of transition probabilities in the form:
(a) Set up the matrix of transition probabilities in the form: 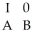 (b) Determine the fundamental matrix for this problem.
(c) What is the probability that an employee who has received a raise will eventually quit?
(d) What is the probability that an employee who has received a raise will eventually be fired?
(b) Determine the fundamental matrix for this problem.
(c) What is the probability that an employee who has received a raise will eventually quit?
(d) What is the probability that an employee who has received a raise will eventually be fired?
(Essay)
4.9/5  (33)
(33)
Table 15-1
The following data consists of a matrix of transition probabilities (P) of three competing companies, and the initial market share π(0). Assume that each state represents a company (Company 1, Company 2, Company 3, respectively) and the transition probabilities represent changes from one month to the next.
P =  π(0) = (0.3, 0.6, 0.1)
-Using the data in Table 15-1, determine Company 2's estimated market share in the next period.
π(0) = (0.3, 0.6, 0.1)
-Using the data in Table 15-1, determine Company 2's estimated market share in the next period.
(Multiple Choice)
4.8/5  (37)
(37)
The vector of state probabilities for any period is equal to the vector of state probabilities for the preceding period multiplied by the matrix of transition probabilities.
(True/False)
4.9/5  (42)
(42)
The weather is becoming important to you since you would like to go on a picnic today. If it was sunny yesterday, there is a 70% chance it will be sunny today. If it was raining yesterday, there is a 30% chance it will be sunny today. If the probability that it was raining yesterday is 0.25, what is the probability that it will rain today?
(Multiple Choice)
4.7/5  (40)
(40)
For any absorbing state, the probability that a state will remain unchanged in the future is one.
(True/False)
4.9/5  (38)
(38)
Creating the fundamental matrix requires a partition of the matrix of transition.
(True/False)
4.8/5  (46)
(46)
The matrix of transition probabilities gives the conditional probabilities of moving from one state to another.
(True/False)
4.9/5  (43)
(43)
A Markov process could be used as a model of how a disease progresses from one set of symptoms to another.
(True/False)
4.9/5  (32)
(32)
There is a 60% chance that customer without a smart phone will buy one this year. There is a 95% chance that a customer with a smart phone will continue with a smart phone going into the next year. If 30% of target market currently own smart phones, what is the long run percentage of the target market that will own smart phones?
(Short Answer)
4.9/5  (42)
(42)
Occasionally, a state is entered that will not allow going to any other state in the future. This is called
(Multiple Choice)
4.9/5  (47)
(47)
Markov analysis assumes that there are a limited number of states in the system.
(True/False)
4.9/5  (42)
(42)
Given the following matrix of transition probabilities, write three equations that, when solved, will give the equilibrium state values.
P = 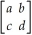
(Essay)
4.9/5  (33)
(33)
Showing 21 - 40 of 78
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)