Exam 15: Markov Analysis

A collection of all state probabilities for a given system at any given period of time is called the

There is a 30% chance that any current client of company A will switch to company B this year. There is a 20% chance that any client of company B will switch to company A this year. If these probabilities are stable over the years, and if company A has 1000 clients and company B has 1000 clients, in the long run (assuming the probabilities do not change), what will the market shares be?

In Markov analysis, states must be collectively exhaustive and mutually exclusive.

A certain utility firm has noticed that a residential customer's bill for one month is dependent on the previous month's bill. The observations are summarized in the following transition matrix. 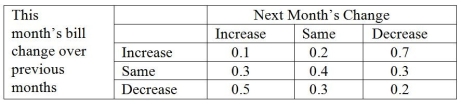The utility company would like to know the long-run probability that a customer's bill will increase, the probability the bill will stay the same, and the probability the bill will decrease.

In Markov analysis, to find the vector of state probabilities for any period,

Given the following vector of state probabilities and the accompanying matrix of transition probabilities, find the next period vector of state probabilities. (0.4 0.4 0.2)

Collectively exhaustive means that a system can be in only one state at any point in time.

The fax machine in an office is very unreliable. If it was working yesterday, there is an 90% chance it will work today. If it was not working yesterday, there is a 5% chance it will work today. (a) What is the probability that it is not working today, if it was not working yesterday? (b) If it was working yesterday, what is the probability that it is working today?

The four basic assumptions of Markov analysis are: 1. There are a limited or finite number of possible states. 2. The probability of changing states remains the same over time. 3. A future state is predictable from previous state and transition matrix. 4. The size and makeup of the system are constant during analysis.

When absorbing states exist, the fundamental matrix is used to compute equilibrium conditions.

Markov analysis might be effectively used for

Equilibrium state probabilities may be estimated by using Markov analysis for a large number of periods.

Table 15-3 Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium. This state contains three cities: Chaos (C₁), Frenzy (C₂), and Tremor (C₃). A transition matrix, indicating the probability that a resident in one city will travel to another, is given below. Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis. C F T Transition matrix: π(0) = [100, 100, 100] -Using the data given in Table 15-3, what is the equilibrium travel population of Chaos (rounded to the nearest whole person)?

Over any given month, Hammond Market loses 10% of its customers to Otro Plaza and 20% to Tres Place. Otro Plaza loses 5% to Hammond and 10% to Tres Place. Tres Place loses 5% of its customers to each of the two competitors. At the present time, Hammond Market has 40% of the market, while the others have 30% each. (a) Next month, what will the market shares be for the three firms? (b) In two months, what will the market shares be for the three firms?

The vector of state probabilities gives the probability of being in particular states at a particular point in time.

"Events" are used to identify all possible conditions of a process or a system.

In a matrix of transition probabilities (where i equals the row number and j equals the column number),

Describe the concept of "mutually exclusive" in the context of Markov analysis.