Exam 8: Linear Programming Applications
Exam 1: Introduction to Quantitative Analysis63 Questions
Exam 2: Probability Concepts and Applications145 Questions
Exam 3: Decision Analysis119 Questions
Exam 4: Regression Models120 Questions
Exam 5: Forecasting101 Questions
Exam 6: Inventory Control Models113 Questions
Exam 7: Linear Programming Models: Graphical and Computer Methods100 Questions
Exam 8: Linear Programming Applications96 Questions
Exam 9: Transportation and Assignment Models80 Questions
Exam 10: Integer Programming, Goal Programming, and Nonlinear Programming88 Questions
Exam 11: Network Models86 Questions
Exam 12: Project Management123 Questions
Exam 13: Waiting Lines and Queuing Theory Models133 Questions
Exam 14: Simulation Modeling68 Questions
Exam 15: Markov Analysis78 Questions
Exam 16: Statistical Quality Control87 Questions
Select questions type
A cruise line is planning its menu for the next trip. Vacationers like eating steak, lobster, and chicken. The cruise line has decided to plan for at least half of all booked passengers to have a steak dinner, for at least a quarter of all passengers to have lobster, and the rest to have chicken. Steak dinners cost the company $8, lobsters cost $15, and chicken costs the line $4. On the next cruise, there are 400 passengers booked. In addition, the cruise line has decided to plan for an additional 25% more meals than bookings. Formulate the appropriate linear program. 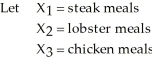
(Essay)
4.8/5  (29)
(29)
In general, linear programming is unable to solve complex labor planning as the objective function is usually not definable.
(True/False)
4.8/5  (32)
(32)
Which of the following is considered a decision variable in the production mix problem of maximizing profit?
(Multiple Choice)
4.7/5  (38)
(38)
Which of the following is considered a decision variable in the media selection problem of minimizing interview costs in surveying?
(Multiple Choice)
4.9/5  (36)
(36)
Three types of gasoline are manufactured by a company - Regular, Super, and Extra. Regular should have at least 11 percent additive 1 and 17 percent additive 2. Super should have at least 13 percent additive 1 and 22 percent additive 2. Extra should have at least 17 percent additive 1 and 19 percent additive 2. These are made by using two crudes - A and B. Crude A cost $28 per barrel and is 14 percent additive 1 and 18 percent additive 2. Crude B costs $30 per barrel and is 20 percent additive 1 and 24 percent additive 2. The demand for Regular is projected to be 1,000 barrels, while each of the others has a demand of 2,000 barrels. Formulate this as a linear programming problem to minimize cost while meeting all constraints. Carefully define all decision variables.
(Essay)
4.8/5  (36)
(36)
In a production scheduling problem, the inventory at the end of this month is set equal to the inventory at the end of last month + last month's production − sales this month.
(True/False)
4.7/5  (28)
(28)
The linear programming approach to media selection problems is typically to either maximize the number of ads placed per week or to minimize advertising costs.
(True/False)
4.8/5  (41)
(41)
Table 8-1
A small furniture manufacturer produces tables and chairs. Each product must go through three stages of the manufacturing process: assembly, finishing, and inspection. Each table requires 3 hours of assembly, 2 hours of finishing, and 1 hour of inspection. Each chair requires 2 hours of assembly, 2 hours of finishing, and 1 hour of inspection. The profit per table is $120 while the profit per chair is $80. Currently, each week there are 200 hours of assembly time available, 180 hours of finishing time, and 40 hours of inspection time. Linear programming is to be used to develop a production schedule. Define the variables as follows: 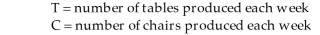 -According to Table 8-1, which describes a production problem, which of the following would be a necessary constraint in the problem?
-According to Table 8-1, which describes a production problem, which of the following would be a necessary constraint in the problem?
(Multiple Choice)
4.8/5  (39)
(39)
A media selection LP application describes a method in which media producers select customers.
(True/False)
4.9/5  (37)
(37)
A manufacturer of microcomputers produces four models: Portable, Student, Office, and Network. The profit per unit on each of these four models is $500, $350, $700, and $1000, respectively. The models require the labor and materials per unit shown below. 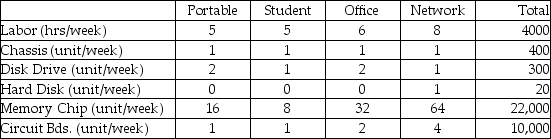 Formulate this product mix problem using linear programming.
Formulate this product mix problem using linear programming.
(Essay)
4.8/5  (30)
(30)
Production scheduling is amenable to solution by LP because it is a problem that must be solved on a regular basis.
(True/False)
4.8/5  (38)
(38)
Green Grass, Inc. just ran out of stock and suddenly has two emergency orders for grass seed blends: one is for 1500 pounds of normal, the other for 2300 pounds of special. At least each pound of normal should contain 60 percent annual seed, while each pound of special should contain at least 70 percent perennial seed. Green Grass has two input mixtures, A and B. Mixture A contains 80 percent perennial and 15 percent annual seed. Mixture B contains 70 percent annual and 25 percent perennial seed. Mixture A costs 90 cents per pound and mixture B costs 50 cents per pound. Set up the constraints and the objective function to solve this blending problem. 
(Essay)
4.8/5  (42)
(42)
A small furniture manufacturer produces tables and chairs. Each product must go through three stages of the manufacturing process: assembly, finishing, and inspection. Each table requires 3 hours of assembly, 2 hours of finishing, and 1 hour of inspection. Each chair requires 2 hours of assembly, 2 hours of finishing, and 1 hour of inspection. The profit per table is $120, while the profit per chair is $80. Currently, each week there are 200 hours of assembly time available, 180 hours of finishing time, and 40 hours of inspection time. To keep a balance, the number of chairs produced should be at least twice the number of tables. Also, the number of chairs cannot exceed six times the number of tables. How many tables and chairs should the furniture manufacturer produce to maximize profit?
(Essay)
4.9/5  (38)
(38)
The selection of specific investments from among a wide variety of alternatives is the type of LP problem known as
(Multiple Choice)
4.8/5  (36)
(36)
A small furniture manufacturer produces tables and chairs. Each product must go through three stages of the manufacturing process: assembly, finishing, and inspection. Each table requires 3 hours of assembly, 2 hours of finishing, and 1 hour of inspection. Each chair requires 2 hours of assembly, 2 hours of finishing, and 1 hour of inspection. The profit per table is $120, while the profit per chair is $80. Currently, each week there are 200 hours of assembly time available, 180 hours of finishing time, and 40 hours of inspection time. To keep a balance, the number of chairs produced should be at least twice the number of tables. Also, the number of chairs cannot exceed six times the number of tables. Formulate this as a linear programming problem. Carefully define all decision variables.
(Essay)
4.8/5  (30)
(30)
Blending problems arise when one must decide which of two or more ingredients is to be chosen to produce a product.
(True/False)
4.7/5  (37)
(37)
Table 8-3
Each coffee table produced by Timothy Kent Designers nets the firm a profit of $9. Each bookcase yields a $12 profit. Kent's firm is small and its resources limited. During any given production period (of 1 week), 10 gallons of varnish and 12 lengths of high quality redwood are available. Each coffee table requires approximately 1 gallon of varnish and 1 length of redwood. Each bookcase takes 1 gallon of varnish and 2 lengths of wood. 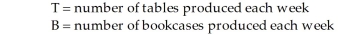 -Referring to Table 8-3, which of the following constraints would be used?
-Referring to Table 8-3, which of the following constraints would be used?
(Multiple Choice)
4.8/5  (37)
(37)
The following does not represent a factor a manager might typically consider when employing linear programming for a production scheduling:
(Multiple Choice)
4.8/5  (33)
(33)
Showing 61 - 80 of 96
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)