Exam 8: Linear Programming Applications

Which of the following statements is false regarding the portfolio selection problem?

When formulating transportation LP problems, the objective function usually deals with the

Which of the following statements is true regarding the labor planning problem?

Table 8-1 A small furniture manufacturer produces tables and chairs. Each product must go through three stages of the manufacturing process: assembly, finishing, and inspection. Each table requires 3 hours of assembly, 2 hours of finishing, and 1 hour of inspection. Each chair requires 2 hours of assembly, 2 hours of finishing, and 1 hour of inspection. The profit per table is $120 while the profit per chair is $80. Currently, each week there are 200 hours of assembly time available, 180 hours of finishing time, and 40 hours of inspection time. Linear programming is to be used to develop a production schedule. Define the variables as follows: 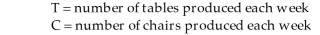-According to Table 8-1, which describes a production problem, suppose it is decided that there must be 4 chairs produced for every table. How would this constraint be written?

The selection of specific media from among a wide variety of alternatives is the type of LP problem known as

Three types of fertilizer are manufactured by a company: Regular, Supergro, and Jungle Feeder. Regular should have at least 10 percent nitrogen and 16 percent phosphorous. Supergro should have at least 12 percent nitrogen and 20 percent phosphorous, and Jungle Feeder should have at least 15 percent nitrogen and 18 percent phosphorous. These are made by using two components: A and B. Component A costs $0.30 per pound and is 14 percent nitrogen and 18 percent phosphorous. Component B costs $0.50 per pound and is 20 percent nitrogen and 24 percent phosphorous. The demand for Regular is projected to be 1,000 pounds, while each of the others has a demand of 2,000 pounds. Formulate the appropriate linear program.

If a linear programming problem has alternate solutions, the order in which you enter the constraints may affect the particular solution found.

Table 8-5 Ivana Myrocle wishes to invest her inheritance of $200,000 so that her return on investment is maximized, but she also wishes to keep her risk level relatively low. She has decided to invest her money in any of three possible ways: CDs, which pay a guaranteed 6 percent; stocks, which have an expected return of 13 percent; and a money market mutual fund, which is expected to return 8 percent. She has decided that any or all of the $200,000 may be invested, but any part (or all) of it may be put in any of the 3 alternatives. Thus, she may have some money invested in all three alternatives. In formulating this as a linear programming problem, define the variables as follows: 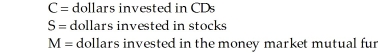-According to Table 8-5, which describes an investment problem, suppose that Ivana has decided that the amount invested in stocks cannot exceed one-fourth of the total amount invested. Which is the best way to write this constraint?

Table 8-5 Ivana Myrocle wishes to invest her inheritance of $200,000 so that her return on investment is maximized, but she also wishes to keep her risk level relatively low. She has decided to invest her money in any of three possible ways: CDs, which pay a guaranteed 6 percent; stocks, which have an expected return of 13 percent; and a money market mutual fund, which is expected to return 8 percent. She has decided that any or all of the $200,000 may be invested, but any part (or all) of it may be put in any of the 3 alternatives. Thus, she may have some money invested in all three alternatives. In formulating this as a linear programming problem, define the variables as follows: 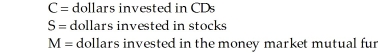-According to Table 8-5, which describes an investment problem, suppose that Ivana has assigned the following risk factors to each investment instrument CDs (C): 1.2; stocks (S): 4.8; money market mutual fund (M): 3.2. If Ivana decides that she wants the risk factor for the whole investment to be less than 3.3, how should the necessary constraint be written?

Table 8-2 A small furniture manufacturer produces tables and chairs. Each product must go through three stages of the manufacturing process: assembly, finishing, and inspection. Each table requires 4 hours of assembly, 3 hours of finishing, and 1 hour of inspection. Each chair requires 3 hours of assembly, 2 hours of finishing, and 2 hours of inspection. The selling price per table is $140 while the selling price per chair is $90. Currently, each week there are 220 hours of assembly time available, 160 hours of finishing time, and 45 hours of inspection time. Assume that one hour of assembly time costs $5.00; one hour of finishing time costs $6.00; one hour of inspection time costs $4.50; and that whatever labor hours are not required for the table and chairs can be applied to another product. Linear programming is to be used to develop a production schedule. Define the variables as follows: 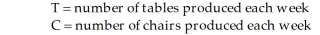-According to Table 8-2, which describes a production problem, suppose you realize that you can trade off assembly hours for finishing hours, but that the total number of finishing hours, including the trade-off hours, cannot exceed 240 hours. How would this constraint be written?

The following problem type is such a special case of linear programming that a special algorithm has been developed to solve it:

The linear programming model of the production scheduling process can include the impact of hiring and layoffs, regular and overtime pay rates, and the desire to have a constant and stable production schedule over a several-month period.

When formulating transportation LP problems, constraints usually deal with the

A fast food restaurant uses full-time and part-time help to meet fluctuating demand during the day. The following table presents projected need for workers at different times of the day: 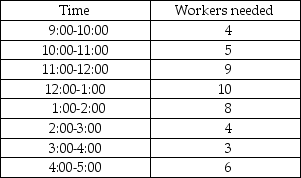There is a maximum of four full-time workers and the other workers are part-time workers. Each full-time worker is there from 9:00 until 5:00, while the part-time workers will work for 4 consecutive hours at a cost of $4.00 per hour. The cost of the full-time worker is $50 per day. The company wishes to minimize total cost while meeting the demands. Formulate this as a linear programming problem. Carefully define all decision variables.

A computer start-up named Pear is considering entering the U.S. market with what they believe to be a smaller and faster computer than some of the existing products on the market. They want to get a feel for whether or not customers would be willing to switch from some of the existing bigger brands to consider their product. They want to collect a reasonable sample from across the U.S. representative of all age brackets. They have split the U.S. into 2 regions: East and West. They want to at least 65% of their sample to cover the East and no fewer than 25% of the West. They also have divided the age groups into 3 categories: 18-35, 36-69, and 70 and up. They want at least 50% of their sample to be between 18-35 and at least 40% to be between 36-69. The costs per person surveyed is given in the table below: Assume that exactly 1,000 people are to be surveyed. How many people should Pear Company survey from each age bracket within each region in order to minimize costs while meeting all requirements?

Table 8-1 A small furniture manufacturer produces tables and chairs. Each product must go through three stages of the manufacturing process: assembly, finishing, and inspection. Each table requires 3 hours of assembly, 2 hours of finishing, and 1 hour of inspection. Each chair requires 2 hours of assembly, 2 hours of finishing, and 1 hour of inspection. The profit per table is $120 while the profit per chair is $80. Currently, each week there are 200 hours of assembly time available, 180 hours of finishing time, and 40 hours of inspection time. Linear programming is to be used to develop a production schedule. Define the variables as follows: 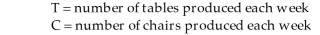-According to Table 8-1, which describes a production problem, suppose it is decided that the number of hours used in the assembly process must be at least 80 percent of the time available. How would this constraint be written?