Exam 7: Linear Programming Models: Graphical and Computer Methods

Suppose a linear programming (maximization) problem has been solved and the optimal value of the objective function is $300. Suppose a constraint is removed from this problem. Explain how this might affect each of the following: (a) the feasible region. (b) the optimal value of the objective function.

Which of the following is not an assumption of LP?

Consider a product mix problem, where the decision involves determining the optimal production levels for products X and Y. A unit of X requires 4 hours of labor in department 1 and 6 hours a labor in department 2. A unit of Y requires 3 hours of labor in department 1 and 8 hours of labor in department 2. Currently, 1000 hours of labor time are available in department 1, and 1200 hours of labor time are available in department 2. Furthermore, 400 additional hours of cross-trained workers are available to assign to either department (or split between both). Each unit of X sold returns a $50 profit, while each unit of Y sold returns a $60 profit. All units produced can be sold. Formulate this problem as a linear program. (Hint: Consider introducing other decision variables in addition to the production amounts for X and Y.)

The set of solution points that satisfies all of a linear programming problem's constraints simultaneously is defined as the feasible region in graphical linear programming.

Consider the following linear program: 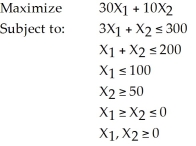(a) Solve the problem graphically. Is there more than one optimal solution? Explain. (b) Are there any redundant constraints?

Which of the following is not a property of all linear programming problems?

There are no limitations on the number of constraints or variables that can be graphed to solve an LP problem.

One basic assumption of linear programming is proportionality. Explain its need.

Two advertising media are being considered for promotion of a product. Radio ads cost $400 each, while newspaper ads cost $600 each. The total budget is $7,200 per week. The total number of ads should be at least 15, with at least 2 of each type, and there should be no more than 19 ads in total. The company does not want the number of newspaper ads to exceed the number of radio ads by more than 25 percent. Each newspaper ad reaches 6,000 people, 50 percent of whom will respond; while each radio ad reaches 2,000 people, 20 percent of whom will respond. The company wishes to reach as many respondents as possible while meeting all the constraints stated. Develop the appropriate LP model for determining the number of ads of each type that should be placed.

Consider the following linear programming problem: 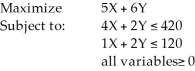Which of the following points (X,Y) is not feasible?

One of the assumptions of LP is "proportionality."

One of the assumptions of LP is "simultaneity."

Which of the following functions is not linear?

The condition when there is no solution that satisfies all the constraints simultaneously is called

Consider the following linear programming problem: 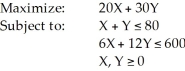This is a special case of a linear programming problem in which

Any time that we have an isoprofit line that is parallel to a constraint, we have the possibility of multiple solutions.

Which of the following is not a property of linear programs?

Sensitivity analysis enables us to look at the effects of changing the coefficients in the objective function, one at a time.

A furniture company is producing two types of furniture. Product A requires 8 board feet of wood and 2 lbs of wicker. Product B requires 6 board feet of wood and 6 lbs of wicker. There are 2000 board feet of wood available for product and 1000 lbs of wicker. Product A earns a profit margin of $30 a unit and Product B earns a profit margin of $40 a unit. Formulate the problem as a linear program.

Consider the following linear programming problem: 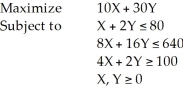This is a special case of a linear programming problem in which