Exam 7: Linear Programming Models: Graphical and Computer Methods
Exam 1: Introduction to Quantitative Analysis63 Questions
Exam 2: Probability Concepts and Applications145 Questions
Exam 3: Decision Analysis119 Questions
Exam 4: Regression Models120 Questions
Exam 5: Forecasting101 Questions
Exam 6: Inventory Control Models113 Questions
Exam 7: Linear Programming Models: Graphical and Computer Methods100 Questions
Exam 8: Linear Programming Applications96 Questions
Exam 9: Transportation and Assignment Models80 Questions
Exam 10: Integer Programming, Goal Programming, and Nonlinear Programming88 Questions
Exam 11: Network Models86 Questions
Exam 12: Project Management123 Questions
Exam 13: Waiting Lines and Queuing Theory Models133 Questions
Exam 14: Simulation Modeling68 Questions
Exam 15: Markov Analysis78 Questions
Exam 16: Statistical Quality Control87 Questions
Select questions type
Consider the following linear programming problem: 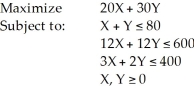 This is a special case of a linear programming problem in which
This is a special case of a linear programming problem in which
(Multiple Choice)
4.8/5  (38)
(38)
The mathematical theory behind linear programming states that an optimal solution to any problem will lie at a(n) ________ of the feasible region.
(Multiple Choice)
4.8/5  (37)
(37)
In the term linear programming, the word programming comes from the phrase "computer programming."
(True/False)
4.8/5  (34)
(34)
Consider the following linear programming problem: 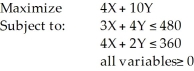 The feasible corner points are (48,84), (0,120), (0,0), (90,0). What is the maximum possible value for the objective function?
The feasible corner points are (48,84), (0,120), (0,0), (90,0). What is the maximum possible value for the objective function?
(Multiple Choice)
4.8/5  (39)
(39)
Determine where the following two constraints intersect.
2X - 4Y = 800
−X + 6Y ≥ -200
(Short Answer)
4.7/5  (35)
(35)
The existence of non-negativity constraints in a two-variable linear program implies that we are always working in the northwest quadrant of a graph.
(True/False)
4.8/5  (40)
(40)
Consider the following linear programming problem: 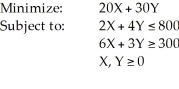 What is the optimum solution to this problem (X,Y)?
What is the optimum solution to this problem (X,Y)?
(Multiple Choice)
4.7/5  (40)
(40)
What type of problems use LP to decide how much of each product to make, given a series of resource restrictions?
(Multiple Choice)
4.9/5  (36)
(36)
Consider the following linear programming problem: 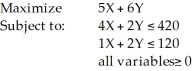 Which of the following points (X,Y) is feasible?
Which of the following points (X,Y) is feasible?
(Multiple Choice)
4.9/5  (28)
(28)
When two or more constraints conflict with one another, we have a condition called unboundedness.
(True/False)
4.9/5  (32)
(32)
An objective function is necessary in a maximization problem but is not required in a minimization problem.
(True/False)
4.9/5  (32)
(32)
Solve the following linear programming problem using the corner point method: 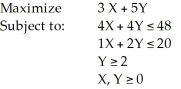
(Essay)
4.8/5  (33)
(33)
In a linear program, the constraints must be linear, but the objective function may be nonlinear.
(True/False)
4.9/5  (33)
(33)
Consider the following constraints from a linear programming problem: 2X + Y ≤ 200
X + 2Y ≤ 200
X, Y ≥ 0
If these are the only constraints, which of the following points (X,Y) cannot be the optimal solution?
(Multiple Choice)
4.8/5  (38)
(38)
In some instances, an infeasible solution may be the optimum found by the corner point method.
(True/False)
4.8/5  (38)
(38)
If one changes the contribution rates in the objective function of an LP,
(Multiple Choice)
4.8/5  (47)
(47)
Showing 21 - 40 of 100
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)