Exam 15: Multiple Regression Model Building
Exam 1: Defining and Collecting Data189 Questions
Exam 3: Numerical Descriptive Measures184 Questions
Exam 4: Basic Probability156 Questions
Exam 5: Discrete Probability Distributions218 Questions
Exam 6: The Normal Distribution and Other Continuous Distributions189 Questions
Exam 7: Sampling Distributions127 Questions
Exam 8: Confidence Interval Estimation196 Questions
Exam 9: Fundamentals of Hypothesis Testing: One-Sample Tests170 Questions
Exam 10: Two-Sample Tests210 Questions
Exam 11: Analysis of Variance130 Questions
Exam 12: Chi-Square Tests and Nonparametric Tests175 Questions
Exam 13: Simple Linear Regression213 Questions
Exam 14: Introduction to Multiple Regression337 Questions
Exam 15: Multiple Regression Model Building96 Questions
Exam 16: Time-Series Forecasting165 Questions
Exam 17: A Roadmap for Analyzing Data303 Questions
Exam 18: Statistical Applications in Quality Management130 Questions
Exam 19: Decision Making126 Questions
Exam 20: Index Numbers44 Questions
Exam 21: Chi-Square Tests for the Variance or Standard Deviation11 Questions
Exam 22: Mcnemar Test for the Difference Between Two Proportions Related Samples15 Questions
Exam 25: The Analysis of Means Anom2 Questions
Exam 23: The Analysis of Proportions Anop3 Questions
Exam 24: The Randomized Block Design85 Questions
Exam 26: The Power of a Test41 Questions
Exam 27: Estimation and Sample Size Determination for Finite Populations13 Questions
Exam 28: Application of Confidence Interval Estimation in Auditing13 Questions
Exam 29: Sampling From Finite Populations20 Questions
Exam 30: The Normal Approximation to the Binomial Distribution27 Questions
Exam 31: Counting Rules14 Questions
Exam 32: Lets Get Started Big Things to Learn First33 Questions
Select questions type
An independent variable Xj is considered highly correlated with the other independent variables if
(Multiple Choice)
4.8/5  (45)
(45)
True or False: Collinearity is present if the dependent variable is linearly related to one of the explanatory variables.
(True/False)
4.7/5  (30)
(30)
TABLE 15-4
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing),daily mean of the percentage of students attending class (% Attendance),mean teacher salary in dollars (Salaries),and instructional spending per pupil in dollars (Spending)of 47 schools in the state.
Let Y = % Passing as the dependent variable,X1 = % Attendance,X2 = Salaries and X3 = Spending.
The coefficient of multiple determination ( 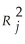 )of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743.
The output from the best-subset regressions is given below:
)of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743.
The output from the best-subset regressions is given below: 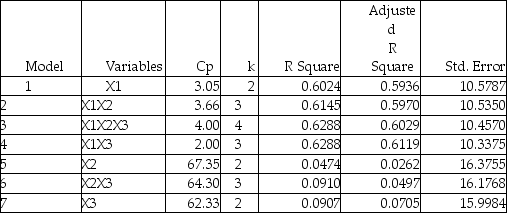 Following is the residual plot for % Attendance:
Following is the residual plot for % Attendance: 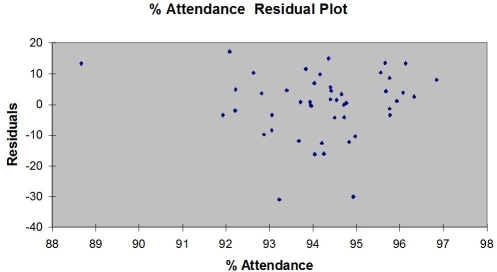 Following is the output of several multiple regression models:
Model (I):
Following is the output of several multiple regression models:
Model (I): 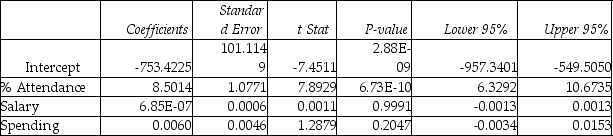 Model (II):
Model (II):  Model (III):
Model (III): 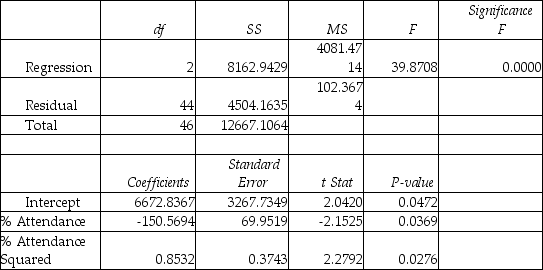 -True or False: Referring to Table 15-4,the null hypothesis should be rejected when testing whether the quadratic effect of daily average of the percentage of students attending class on percentage of students passing the proficiency test is significant at a 5% level of significance.
-True or False: Referring to Table 15-4,the null hypothesis should be rejected when testing whether the quadratic effect of daily average of the percentage of students attending class on percentage of students passing the proficiency test is significant at a 5% level of significance.
(True/False)
4.9/5  (33)
(33)
TABLE 15-6
Given below are results from the regression analysis on 40 observations where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Y)and the independent variables are the age of the worker (X1),the number of years of education received (X2),the number of years at the previous job (X3),a dummy variable for marital status (X4: 1 = married,0 = otherwise),a dummy variable for head of household (X5: 1 = yes,0 = no)and a dummy variable for management position (X6: 1 = yes,0 = no).
The coefficient of multiple determination ( 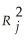 )for the regression model using each of the 6 variables Xj as the dependent variable and all other X variables as independent variables are,respectively,0.2628,0.1240,0.2404,0.3510,0.3342 and 0.0993.
The partial results from best-subset regression are given below:
)for the regression model using each of the 6 variables Xj as the dependent variable and all other X variables as independent variables are,respectively,0.2628,0.1240,0.2404,0.3510,0.3342 and 0.0993.
The partial results from best-subset regression are given below: 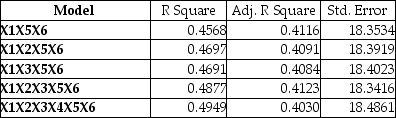 -True or False: Referring to Table 15-6,the variable X1 should be dropped to remove collinearity.
-True or False: Referring to Table 15-6,the variable X1 should be dropped to remove collinearity.
(True/False)
4.9/5  (38)
(38)
TABLE 15-6
Given below are results from the regression analysis on 40 observations where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Y)and the independent variables are the age of the worker (X1),the number of years of education received (X2),the number of years at the previous job (X3),a dummy variable for marital status (X4: 1 = married,0 = otherwise),a dummy variable for head of household (X5: 1 = yes,0 = no)and a dummy variable for management position (X6: 1 = yes,0 = no).
The coefficient of multiple determination ( 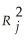 )for the regression model using each of the 6 variables Xj as the dependent variable and all other X variables as independent variables are,respectively,0.2628,0.1240,0.2404,0.3510,0.3342 and 0.0993.
The partial results from best-subset regression are given below:
)for the regression model using each of the 6 variables Xj as the dependent variable and all other X variables as independent variables are,respectively,0.2628,0.1240,0.2404,0.3510,0.3342 and 0.0993.
The partial results from best-subset regression are given below:  -True or False: Referring to Table 15-6,the variable X2 should be dropped to remove collinearity.
-True or False: Referring to Table 15-6,the variable X2 should be dropped to remove collinearity.
(True/False)
4.9/5  (27)
(27)
TABLE 15-6
Given below are results from the regression analysis on 40 observations where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Y)and the independent variables are the age of the worker (X1),the number of years of education received (X2),the number of years at the previous job (X3),a dummy variable for marital status (X4: 1 = married,0 = otherwise),a dummy variable for head of household (X5: 1 = yes,0 = no)and a dummy variable for management position (X6: 1 = yes,0 = no).
The coefficient of multiple determination ( 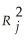 )for the regression model using each of the 6 variables Xj as the dependent variable and all other X variables as independent variables are,respectively,0.2628,0.1240,0.2404,0.3510,0.3342 and 0.0993.
The partial results from best-subset regression are given below:
)for the regression model using each of the 6 variables Xj as the dependent variable and all other X variables as independent variables are,respectively,0.2628,0.1240,0.2404,0.3510,0.3342 and 0.0993.
The partial results from best-subset regression are given below:  -True or False: Referring to Table 15-6,the variable X5 should be dropped to remove collinearity.
-True or False: Referring to Table 15-6,the variable X5 should be dropped to remove collinearity.
(True/False)
4.9/5  (28)
(28)
A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies.She proceeds to randomly select 26 large corporations and record information in millions of dollars.A statistical analyst discovers that capital spending by corporations has a significant inverse relationship with wage spending.What should the microeconomist who developed this multiple regression model be particularly concerned with?
(Multiple Choice)
4.8/5  (35)
(35)
True or False: Referring to Table 15-3,suppose the chemist decides to use a t test to determine if there is a significant difference between a linear model and a curvilinear model that includes a linear term.If she used a level of significance of 0.01,she would decide that the linear model is sufficient.
(True/False)
4.8/5  (39)
(39)
TABLE 15-6
Given below are results from the regression analysis on 40 observations where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Y)and the independent variables are the age of the worker (X1),the number of years of education received (X2),the number of years at the previous job (X3),a dummy variable for marital status (X4: 1 = married,0 = otherwise),a dummy variable for head of household (X5: 1 = yes,0 = no)and a dummy variable for management position (X6: 1 = yes,0 = no).
The coefficient of multiple determination ( 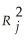 )for the regression model using each of the 6 variables Xj as the dependent variable and all other X variables as independent variables are,respectively,0.2628,0.1240,0.2404,0.3510,0.3342 and 0.0993.
The partial results from best-subset regression are given below:
)for the regression model using each of the 6 variables Xj as the dependent variable and all other X variables as independent variables are,respectively,0.2628,0.1240,0.2404,0.3510,0.3342 and 0.0993.
The partial results from best-subset regression are given below:  -True or False: Referring to Table 15-6,the model that includes X1,X2,X3,X5 and X6 should be among the appropriate models using the Mallow's Cp statistic.
-True or False: Referring to Table 15-6,the model that includes X1,X2,X3,X5 and X6 should be among the appropriate models using the Mallow's Cp statistic.
(True/False)
4.7/5  (34)
(34)
TABLE 15-6
Given below are results from the regression analysis on 40 observations where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Y)and the independent variables are the age of the worker (X1),the number of years of education received (X2),the number of years at the previous job (X3),a dummy variable for marital status (X4: 1 = married,0 = otherwise),a dummy variable for head of household (X5: 1 = yes,0 = no)and a dummy variable for management position (X6: 1 = yes,0 = no).
The coefficient of multiple determination ( 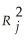 )for the regression model using each of the 6 variables Xj as the dependent variable and all other X variables as independent variables are,respectively,0.2628,0.1240,0.2404,0.3510,0.3342 and 0.0993.
The partial results from best-subset regression are given below:
)for the regression model using each of the 6 variables Xj as the dependent variable and all other X variables as independent variables are,respectively,0.2628,0.1240,0.2404,0.3510,0.3342 and 0.0993.
The partial results from best-subset regression are given below:  -True or False: Referring to Table 15-6,the model that includes X1,X2,X5 and X6 should be among the appropriate models using the Mallow's Cp statistic.
-True or False: Referring to Table 15-6,the model that includes X1,X2,X5 and X6 should be among the appropriate models using the Mallow's Cp statistic.
(True/False)
4.8/5  (32)
(32)
True or False: One of the consequences of collinearity in multiple regression is inflated standard errors in some or all of the estimated slope coefficients.
(True/False)
4.8/5  (30)
(30)
TABLE 15-6
Given below are results from the regression analysis on 40 observations where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Y)and the independent variables are the age of the worker (X1),the number of years of education received (X2),the number of years at the previous job (X3),a dummy variable for marital status (X4: 1 = married,0 = otherwise),a dummy variable for head of household (X5: 1 = yes,0 = no)and a dummy variable for management position (X6: 1 = yes,0 = no).
The coefficient of multiple determination ( 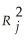 )for the regression model using each of the 6 variables Xj as the dependent variable and all other X variables as independent variables are,respectively,0.2628,0.1240,0.2404,0.3510,0.3342 and 0.0993.
The partial results from best-subset regression are given below:
)for the regression model using each of the 6 variables Xj as the dependent variable and all other X variables as independent variables are,respectively,0.2628,0.1240,0.2404,0.3510,0.3342 and 0.0993.
The partial results from best-subset regression are given below:  -True or False: Referring to Table 15-6,the model that includes all the six independent variables should be among the appropriate models using the Mallow's Cp statistic.
-True or False: Referring to Table 15-6,the model that includes all the six independent variables should be among the appropriate models using the Mallow's Cp statistic.
(True/False)
4.9/5  (29)
(29)
TABLE 15-5
What are the factors that determine the acceleration time (in sec.)from 0 to 60 miles per hour of a car? Data on the following variables for 171 different vehicle models were collected:
Accel Time: Acceleration time in sec.
Cargo Vol: Cargo volume in cu.ft.
HP: Horsepower
MPG: Miles per gallon
SUV: 1 if the vehicle model is an SUV with Coupe as the base when SUV and Sedan are both 0
Sedan: 1 if the vehicle model is a sedan with Coupe as the base when SUV and Sedan are both 0
The coefficient of multiple determination ( 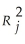 )for the regression model using each of the 5 variables Xj as the dependent variable and all other X variables as independent variables are,respectively,0.7461,0.5676,0.6764,0.8582,0.6632.
-Referring to Table 15-5,what is the value of the variance inflationary factor of Cargo Vol?
)for the regression model using each of the 5 variables Xj as the dependent variable and all other X variables as independent variables are,respectively,0.7461,0.5676,0.6764,0.8582,0.6632.
-Referring to Table 15-5,what is the value of the variance inflationary factor of Cargo Vol?
(Short Answer)
4.8/5  (34)
(34)
TABLE 15-4
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing),daily mean of the percentage of students attending class (% Attendance),mean teacher salary in dollars (Salaries),and instructional spending per pupil in dollars (Spending)of 47 schools in the state.
Let Y = % Passing as the dependent variable,X1 = % Attendance,X2 = Salaries and X3 = Spending.
The coefficient of multiple determination ( 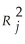 )of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743.
The output from the best-subset regressions is given below:
)of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743.
The output from the best-subset regressions is given below:  Following is the residual plot for % Attendance:
Following is the residual plot for % Attendance:  Following is the output of several multiple regression models:
Model (I):
Following is the output of several multiple regression models:
Model (I):  Model (II):
Model (II):  Model (III):
Model (III):  -Referring to Table 15-4,the better model using a 5% level of significance derived from the "best" model above is
-Referring to Table 15-4,the better model using a 5% level of significance derived from the "best" model above is
(Multiple Choice)
4.7/5  (37)
(37)
True or False: In data mining where huge data sets are being explored to discover relationships among a large number of variables,the best-subsets approach is more practical than the stepwise regression approach.
(True/False)
4.9/5  (31)
(31)
True or False: Using the Cp statistic in model building,all models with Cp ≤ (k + 1)are equally good.
(True/False)
4.8/5  (32)
(32)
TABLE 15-4
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing),daily mean of the percentage of students attending class (% Attendance),mean teacher salary in dollars (Salaries),and instructional spending per pupil in dollars (Spending)of 47 schools in the state.
Let Y = % Passing as the dependent variable,X1 = % Attendance,X2 = Salaries and X3 = Spending.
The coefficient of multiple determination ( 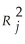 )of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743.
The output from the best-subset regressions is given below:
)of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743.
The output from the best-subset regressions is given below:  Following is the residual plot for % Attendance:
Following is the residual plot for % Attendance:  Following is the output of several multiple regression models:
Model (I):
Following is the output of several multiple regression models:
Model (I):  Model (II):
Model (II):  Model (III):
Model (III):  -Referring to Table 15-4,which of the following models should be taken into consideration using the Mallows' Cp statistic?
-Referring to Table 15-4,which of the following models should be taken into consideration using the Mallows' Cp statistic?
(Multiple Choice)
4.8/5  (33)
(33)
True or False: Referring to Table 15-3,suppose the chemist decides to use an F test to determine if there is a significant curvilinear relationship between time and dose.If she chooses to use a level of significance of 0.01 she would decide that there is a significant curvilinear relationship.
(True/False)
4.8/5  (23)
(23)
True or False: Referring to Table 15-3,suppose the chemist decides to use a t test to determine if there is a significant difference between a linear model and a curvilinear model that includes a linear term.If she used a level of significance of 0.05,she would decide that the linear model is sufficient.
(True/False)
4.7/5  (30)
(30)
Showing 41 - 60 of 96
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)