Exam 3: Modeling and Solving Lp Problems in a Spreadsheet

Exhibit 3.1 The following questions are based on this problem and accompanying Excel windows. Jones Furniture Company produces beds and desks for college students. The production process requires carpentry and varnishing. Each bed requires 6 hours of carpentry and 4 hour of varnishing. Each desk requires 4 hours of carpentry and 8 hours of varnishing. There are 36 hours of carpentry time and 40 hours of varnishing time available. Beds generate $30 of profit and desks generate $40 of profit. Demand for desks is limited, so at most 8 will be produced. Let = Number of Beds to produce = Number of Desks to produce The LP model for the problem is MAX: 30+40 Subject to: 6+4\leq36 (carpentry) 4+8\leq40 (varnishing) \leq8 (demand for desks) ,\geq0 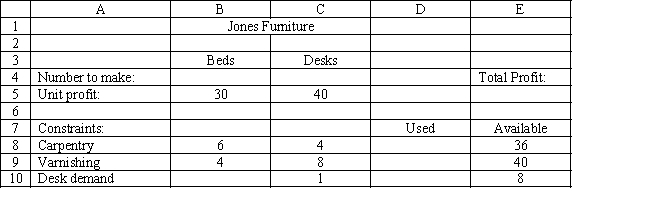-Refer to Exhibit 3.1. What formula should be entered in cell E5 in the accompanying Excel spreadsheet to compute total profit?

A grain store has six types of grain, each varying in cost, quality, and nutritional content. Periodically, excess inventory of these grains are consolidated into two local products, Feed-M-All and Supreme-Feed. Feed-M-All sells for $6.50 for a 10-pound bag while Supreme-Feed sells for $8.50 for a 10-pound bag. These feeds are advertised as having the following nutritional content: Grain Minimum Proten Minimum Fat Maximum Carbohydrates Feed-M-All 16\% 18\% 10\% Supreme-Feed 18\% 18\% 9\% The component grains have the following content characteristics: Grain Cost/10lbs Quality Praten Fat Carbohydrates Paunds Ayail. \ 4.75 4 15\% 10\% 10\% 90 \ 4.00 2 20\% 20\% 8\% 120 \ 3.75 1 10\% 25\% 5\% 150 \ 4.25 3 15\% 20\% 10\% 125 \ 4.50 3 20\% 20\% 10\% 85 \ 5.00 4 25\% 15\% 12\% 165 Targets for Feed-M-All are a cost of $ 4.35 per 10-pound bag, a quality rating of 2.25, along with the minimum percentages of protein and fat, and the maximum percentage of carbohydrates. Similar targets are set for Supreme-Feed with cost set at $ 4.60 and quality at 2.45. There must be at least a 70%-30% mix among these two local feeds. Formulate an LP model for this product mix problem.

Exhibit 3.4 The following questions are based on this problem and accompanying Excel windows. A financial planner wants to design a portfolio of investments for a client. The client has $300,000 to invest and the planner has identified four investment options for the money. The following requirements have been placed on the planner. No more than 25% of the money in any one investment, at least one third should be invested in long-term bonds which mature in seven or more years, and no more than 25% of the total money should be invested in C or D since they are riskier investments. The planner has developed the following LP model based on the data in this table and the requirements of the client. The objective is to maximize the total return of the portfolio. Investment Return Years to Maturity Rating A 6.45\% 9 1-Excellent B 7.10\% 8 2 -Very Good C 8.20\% 5 4 -Fair D 9.00\% 8 3 -Good Let = Dollars invested in A = Dollars invested in B = Dollars invested in C = Dollars invested in D MAX: $\quad .0645 \mathrm { X } _ { 1 } + .071 \mathrm { X } _ { 2 } + .082 \mathrm { X } _ { 3 } + .09 \mathrm { X } _ { 4 }$ Subject to: +++\leq300000 \leq75000 \leq75000 \leq75000 \leq75000 ++\geq100000 +\leq75000 ,,\geq0 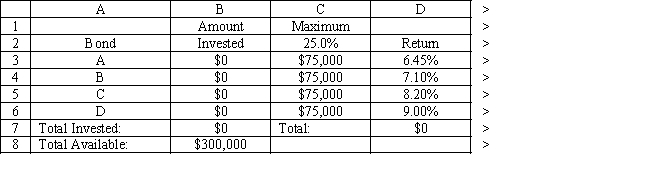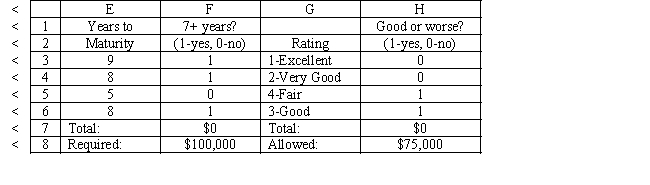-Refer to Exhibit 3.4. Which cells are changing cells in the accompanying Excel spreadsheet?

How many constraints are there in a transportation problem which has 5 supply points and 4 demand points? (ignore the non-negativity constraints)

You have been given the following linear programming model and Excel spreadsheet to solve this problem. What formulas should be entered into cells E5 and D8:D10 to implement this model? MIN: $\quad 8 X _ { 1 } + 3 X _ { 2 }$ Subject to: $\quad X _ { 2 } \geq 8$ 8+5\geq80 3+5\geq60 ,\geq0 A B C D E 1 2 3 4 Number to make: OBJ. FN. VALUE 5 Unit profit: 8 3 6 7 Constraints: Used Available 8 1 1 8 9 2 8 5 80 10 3 3 5 60

What command is used to add the contents of cells A1, A2 and A3?

Exhibit 3.1 The following questions are based on this problem and accompanying Excel windows. Jones Furniture Company produces beds and desks for college students. The production process requires carpentry and varnishing. Each bed requires 6 hours of carpentry and 4 hour of varnishing. Each desk requires 4 hours of carpentry and 8 hours of varnishing. There are 36 hours of carpentry time and 40 hours of varnishing time available. Beds generate $30 of profit and desks generate $40 of profit. Demand for desks is limited, so at most 8 will be produced. Let = Number of Beds to produce = Number of Desks to produce The LP model for the problem is MAX: 30+40 Subject to: 6+4\leq36 (carpentry) 4+8\leq40 (varnishing) \leq8 (demand for desks) ,\geq0 -Refer to Exhibit 3.1. Which cells should be changing cells in this problem?

Exhibit 3.3 The following questions are based on this problem and accompanying Excel windows. Jack's distillery blends scotches for local bars and saloons. One of his customers has requested a special blend of scotch targeted as a bar scotch. The customer wants the blend to involve two scotch products, call them A and B. Product A is a higher quality scotch while product B is a cheaper brand. The customer wants to make the claim the blend is closer to high quality than the alternative. The customer wants 50 1500 ml bottles of the blend. Each bottle must contain at least 48% of Product A and at least 500 ml of B. The customer also specified that the blend have an alcohol content of at least 85%. Product A contains 95% alcohol while product B contains 78%. The blend is sold for $12.50 per bottle. Product A costs $7 per liter and product B costs $3 per liter. The company wants to determine the blend that will meet the customer's requirements and maximize profit. Let $\quad X _ { 1 } =$ Number of liters of product $A _ { 1 }$ in total blend delivered $\quad\quad\quad\mathrm { X } _ { 2 } =$ Number of liters of product $\mathrm { B }$ in total blend delivered MIN: $\quad 7 \mathrm { X } _ { 1 } + 3 \mathrm { X } _ { 2 }$ Subject to: $\quad \mathrm { X } _ { 1 } + \mathrm { X } _ { 2 } = 1.5 * 50$ (Total liters of mix) $\quad\quad\quad\quad\quad\mathrm { X } _ { 1 } \geq 0.48 * 1.5 * 50 \left( \mathrm { X } _ { 1 } \right.$ minimum) $\quad\quad\quad\quad\quad\mathrm { X } _ { 2 } \geq 0.5 ^ { * } 50 \left( \mathrm { X } _ { 2 } \right.$ minimum) $\quad\quad\quad\quad.0 .95 \mathrm { X } _ { 1 } + 0.78 \mathrm { X } _ { 2 } \geq 0.85 * 1.5 * 50$ (85\% alcohol minimum) 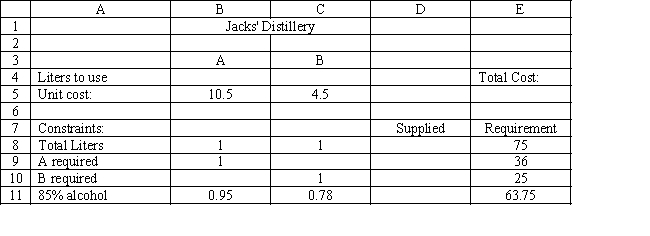$\quad\quad\quad\quad\mathrm { X } _ { 1 } , \mathrm { X } _ { 2 } \geq 0$ -Refer to Exhibit 3.3. What formula should be entered in cell E5 in the accompanying Excel spreadsheet to compute total cost?