Exam 3: Modeling and Solving Lp Problems in a Spreadsheet
Exam 1: Introduction to Modeling and Decision Analysis52 Questions
Exam 2: Introduction to Optimization and Linear Programming62 Questions
Exam 3: Modeling and Solving Lp Problems in a Spreadsheet88 Questions
Exam 4: Sensitivity Analysis and the Simplex Method72 Questions
Exam 5: Network Modeling72 Questions
Exam 6: Integer Linear Programming72 Questions
Exam 7: Goal Programming and Multiple Objective Optimization59 Questions
Exam 8: Nonlinear Programming and Evolutionary Optimization68 Questions
Exam 9: Regression Analysis76 Questions
Exam 10: Discriminant Analysis57 Questions
Exam 11: Time Series Forecasting111 Questions
Exam 12: Introduction to Simulation Using Risk Solver Platform65 Questions
Exam 13: Queuing Theory79 Questions
Exam 14: Decision Analysis102 Questions
Exam 15: Project Management Online61 Questions
Select questions type
Which type of spreadsheet cell represents the left hand sides (LHS) formulas in an LP model?
(Multiple Choice)
4.8/5  (46)
(46)
A hospital needs to determine how many nurses to hire to cover a 24 hour period. The nurses must work 8 consecutive hours but can start work at the start of 6 different shifts. They are paid different wages depending on when they start their shifts. The number of nurses required per 4-hour time period and their wages are shown in the following table.
Time period Required \# of Nurses Wage (\ /) 12-4 20 15 4-8 30 16 am 8-12 40 13 12-4 50 13 4-4 40 14 8-12 30 15
What are the key formulas for this Excel spreadsheet implementation of the following formulation?
Let mumber of nurses warking in thme period
MiN: 1+1+1+1+1+1 Subject ta: 1+1\geq30 1+1\geq40 1+1\geq50 1+1\geq40 1+1\geq30 1+1\geq20 \geq0 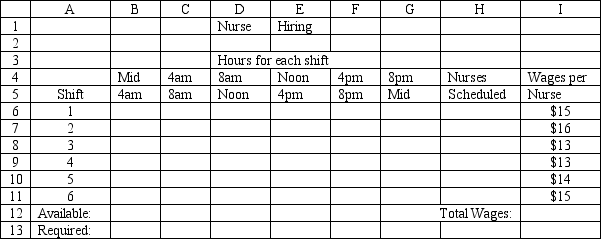
(Essay)
4.7/5  (28)
(28)
Exhibit 3.3
The following questions are based on this problem and accompanying Excel windows.
Jack's distillery blends scotches for local bars and saloons. One of his customers has requested a special blend of scotch targeted as a bar scotch. The customer wants the blend to involve two scotch products, call them A and B. Product A is a higher quality scotch while product B is a cheaper brand. The customer wants to make the claim the blend is closer to high quality than the alternative. The customer wants 50 1500 ml bottles of the blend. Each bottle must contain at least 48% of Product A and at least 500 ml of B. The customer also specified that the blend have an alcohol content of at least 85%. Product A contains 95% alcohol while product B contains 78%. The blend is sold for $12.50 per bottle. Product A costs $7 per liter and product B costs $3 per liter. The company wants to determine the blend that will meet the customer's requirements and maximize profit.
Let Number of liters of product in total blend delivered
Number of liters of product in total blend delivered
MIN:
Subject to: (Total liters of mix)
minimum)
minimum)
(85\% alcohol minimum)
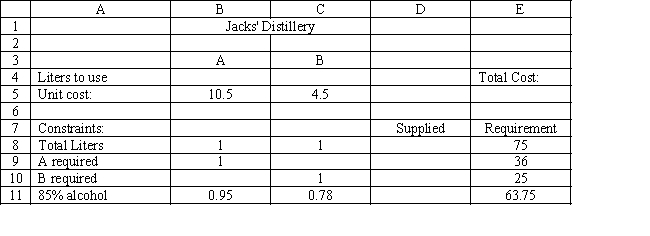 -Refer to Exhibit 3.3. Which of the following statements could represent a constraint in this problem?
-Refer to Exhibit 3.3. Which of the following statements could represent a constraint in this problem?
(Multiple Choice)
4.8/5  (36)
(36)
A paper mill has received an order for rolls of paper. The customer wants 400 12" wide rolls, 300 18" rolls and 200 24" rolls. The company has 40" wide rolls of paper which it can slit to the appropriate width. The company wants to minimize the number of rolls it must use to fill the order.
Formulate the LP for this problem.
(Essay)
4.7/5  (31)
(31)
Exhibit 3.1
The following questions are based on this problem and accompanying Excel windows.
Jones Furniture Company produces beds and desks for college students. The production process requires carpentry and varnishing. Each bed requires 6 hours of carpentry and 4 hour of varnishing. Each desk requires 4 hours of carpentry and 8 hours of varnishing. There are 36 hours of carpentry time and 40 hours of varnishing time available. Beds generate $30 of profit and desks generate $40 of profit. Demand for desks is limited, so at most 8 will be produced.
Let
= Number of Beds to produce = Number of Desks to produce The LP model for the problem is
MAX: 30+40 Subject to: 6+4\leq36 (carpentry) 4+8\leq40 (varnishing) \leq8 (demand for desks) ,\geq0 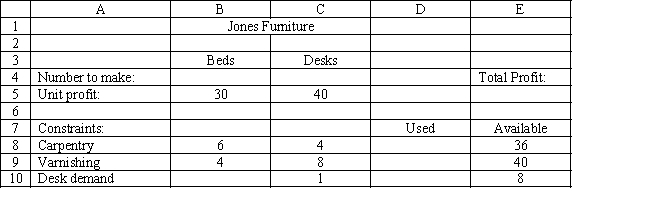 -Refer to Exhibit 3.1. Which cells should be the constraint cells in this problem?
-Refer to Exhibit 3.1. Which cells should be the constraint cells in this problem?
(Multiple Choice)
4.8/5  (38)
(38)
A company needs to purchase several new machines to meet its future production needs. It can purchase three different types of machines A, B, and C. Each machine A costs $80,000 and requires 2,000 square feet of floor space. Each machine B costs $50,000 and requires 3,000 square feet of floor space. Each machine C costs $40,000 and requires 5,000 square feet of floor space. The machines can produce 200, 250 and 350 units per day respectively. The plant can only afford $500,000 for all the machines and has at most 20,000 square feet of room for the machines. The company wants to buy as many machines as possible to maximize daily production.
What values would you enter in the Risk Solver Platform (RSP) task pane for the following cells for this Excel spreadsheet implementation of the formulation for this problem?
Objective Cell:
Variables Cells:
Constraints Cells:
Let mumber of machines of type i purchased
MAX: 200+250+300 Subject to: 2+3+5\leq20 80+50+40\leq500 ,\geq0
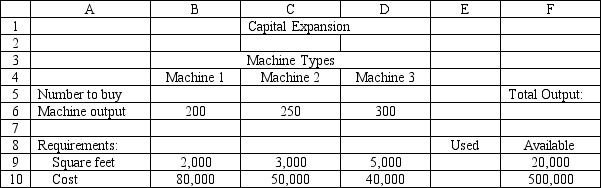
(Essay)
4.9/5  (30)
(30)
Pete's Plastics manufactures plastic at plants in Miami, St. Louis and Cleveland. Pete needs to ship plastic to customers in Pittsburgh, Atlanta and Chicago. He wants to minimize the cost of shipping the plastic from his plants to his customers. The data for the problem is summarized in the following table.
Distance Fram Plants to Customers Plant Pittsburgh Atlanta Chicago Supply Miami 1200 700 1300 30 St. Lauis 700 550 300 40 Cleveland 125 675 350 50 Demand 40 60 20 Formulate the LP for this problem.
(Essay)
4.9/5  (39)
(39)
Microsof Excel, Quattro Pro and Lotus 1-2-3 contain built-in optimizers called
(Multiple Choice)
4.9/5  (40)
(40)
Exhibit 3.5
The following questions are based on this problem and accompanying Excel windows.
A company is planning production for the next 4 quarters. They want to minimize the cost of production. The production cost is stable but demand and production capacity vary from quarter to quarter. The maximum amount of inventory which can be held is 12,000 units and management wants to keep at least 3,000 units on hand. Quarterly inventory holding cost is 3% of the cost of production. The company estimates the number of units carried in inventory each month by averaging the beginning and ending inventory for each month. There are currently 5,000 units in inventory. The company wants to produce at no less than one half of its maximum capacity in any quarter.
1 2 3 4 Unit Production Cost \ 300 \ 300 \ 300 \ 300 Units Demanded 2,000 9,000 12,000 11,000 Maximum Production 8,000 7,000 8,000 9,000 Let = number of units produced in quarter i,i=1,\ldots,4 = beginning inventory for quarter i MiN: 300+300+300+300+ 9 + /2+9 + /2+9 + /2+9 + /2 Subject to: 4000\leq\leq8000 3500\leq\leq7000 4000\leq\leq8000 4500\leq\leq9000 3000\leq+-2000\leq12000 3000\leq+-9000\leq12000 3000\leq+-12000\leq12000 3000\leq+-11000\leq12000 =+-2000 =+-9000 =+-12000 =+-11000 ,\geq0 A 1 Quarter 2 1 2 3 4 3 Beginning Inventory 5,000 11,000 9,000 5,000 4 Units Produced 8,000 7,000 8,000 9,000 5 Units Demanded 2,000 9,000 12,000 11,000 6 Ending Inventory 11,000 9,000 5,000 3,000 7 8 Minimum Procduction 4,000 3,500 4,000 4,500 9 Maximum Froduction 8,000 7,000 8,000 9,000 10 11 Minimum Inventory 3,000 3,000 3,000 3,000 12 Maximum Inventory 12,000 12,000 12,000 12,000 13 14 Unit Production Cost \ 300 \ 300 \ 300 \ 300 15 Unit Carrying Cost 3.0\% \ 9,00 \ 9.00 \ 9,00 \ 9.00 16 17 Quarterly Production Cost \ 2,400,000 \ 2,100,000 \ 2,400,000 \ 2,700,000 18 Quarterly Carrying Cost \ 72,000 \ 90,000 \ 63,000 \ 36,000 19 20 Tota1 Cost \ 9,861,000
-Refer to Exhibit 3.5. What formula should be entered in cell C6 in the accompanying Excel spreadsheet to compute ending inventory?
(Multiple Choice)
4.8/5  (30)
(30)
Exhibit 3.2
The following questions are based on this problem and accompanying Excel windows.
The Byte computer company produces two models of computers, Plain and Fancy. It wants to plan how many computers to produce next month to maximize profits. Producing these computers requires wiring, assembly and inspection time. Each computer produces a certain level of profits but faces only a limited demand. There are also a limited number of wiring, assembly and inspection hours available in each month. The data for this problem is summarized in the following table.
Let Number of Plain computers to produce
Number of Fancy computers to produce
MAX:
Subject to: (wiring hours)
(assembly hours)
(inspection hours)
(Plin computers demand)
(Fancy computers demand)
A B C D E 1 Byte Computer Company 2 3 Plain Fancy 4 Number to make: Total Profit: 5 Unit profit: 30 40 6 7 Constraints: Used Available 8 Wiring 0.4 0.5 50 9 Assembly 0.5 0.4 50 10 Inspection 0.2 0.3 22 11 Plain Demand 1 80 12 Fancy Demand 1 90
-Refer to Exhibit 3.2. Which of the following statements will represent the constraint for just assembly hours?
(Multiple Choice)
4.7/5  (32)
(32)
How many decision variables are there in a transportation problem which has 5 supply points and 4 demand points?
(Multiple Choice)
4.8/5  (36)
(36)
State Farm Supply has just received an order for 10,000 pounds of chicken feed. The farmer has specified certain that the feed meet minimum requirements for Protein, Carbohydrate, Fat and Vitamins. State Farm can blend four different feeds to produce the required mix. The farmer would like to pay the lowest possible price for the feed. The data for the problem is summarized in the following table.
 Formulate the LP for this problem.
Formulate the LP for this problem.
(Essay)
4.8/5  (35)
(35)
A hospital needs to determine how many nurses to hire to cover a 24 hour period. The nurses must work 8 consecutive hours but can start work at the start of 6 different shifts. They are paid different wages depending on when they start their shifts. The number of nurses required per 4-hour time period and their wages are shown in the following table.
Time period Required \# of Nurses Wage (\ /) 12-4 20 15 4-48 30 16 am 8-12 40 13 12-4 50 13 4-4 40 14 8-12 30 15
Formulate the LP for this problem.
(Essay)
4.8/5  (33)
(33)
Exhibit 3.4
The following questions are based on this problem and accompanying Excel windows.
A financial planner wants to design a portfolio of investments for a client. The client has $300,000 to invest and the planner has identified four investment options for the money. The following requirements have been placed on the planner. No more than 25% of the money in any one investment, at least one third should be invested in long-term bonds which mature in seven or more years, and no more than 25% of the total money should be invested in C or D since they are riskier investments. The planner has developed the following LP model based on the data in this table and the requirements of the client. The objective is to maximize the total return of the portfolio.
Investment Return Years to Maturity Rating A 6.45\% 9 1-Excellent B 7.10\% 8 2 -Very Good C 8.20\% 5 4 -Fair D 9.00\% 8 3 -Good Let
= Dollars invested in A = Dollars invested in B = Dollars invested in C = Dollars invested in D
MAX:
Subject to:
+++\leq300000 \leq75000 \leq75000 \leq75000 \leq75000 ++\geq100000 +\leq75000 ,,\geq0 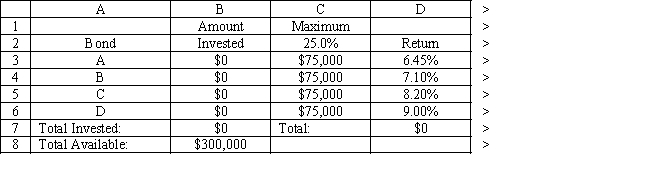
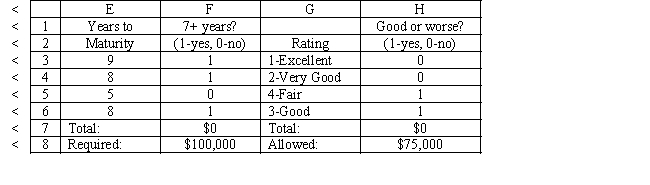 -Refer to Exhibit 3.4. What formula should be entered in cell D7 in the accompanying Excel spreadsheet to compute the total return?
-Refer to Exhibit 3.4. What formula should be entered in cell D7 in the accompanying Excel spreadsheet to compute the total return?
(Multiple Choice)
4.8/5  (39)
(39)
Exhibit 3.3
The following questions are based on this problem and accompanying Excel windows.
Jack's distillery blends scotches for local bars and saloons. One of his customers has requested a special blend of scotch targeted as a bar scotch. The customer wants the blend to involve two scotch products, call them A and B. Product A is a higher quality scotch while product B is a cheaper brand. The customer wants to make the claim the blend is closer to high quality than the alternative. The customer wants 50 1500 ml bottles of the blend. Each bottle must contain at least 48% of Product A and at least 500 ml of B. The customer also specified that the blend have an alcohol content of at least 85%. Product A contains 95% alcohol while product B contains 78%. The blend is sold for $12.50 per bottle. Product A costs $7 per liter and product B costs $3 per liter. The company wants to determine the blend that will meet the customer's requirements and maximize profit.
Let Number of liters of product in total blend delivered
Number of liters of product in total blend delivered
MIN:
Subject to: (Total liters of mix)
minimum)
minimum)
(85\% alcohol minimum)
 -Refer to Exhibit 3.3. What formula should be entered in cell D11 in the accompanying Excel spreadsheet to compute the total liters of alcohol supplied?
-Refer to Exhibit 3.3. What formula should be entered in cell D11 in the accompanying Excel spreadsheet to compute the total liters of alcohol supplied?
(Multiple Choice)
4.9/5  (29)
(29)
Carlton construction is supplying building materials for a new mall construction project in Kansas. Their contract calls for a total of 250,000 tons of material to be delivered over a three-week period. Carlton's supply depot has access to three modes of transportation: a trucking fleet, railway delivery, and air cargo transport. Their contract calls for 120,000 tons delivered by the end of week one, 80% of the total delivered by the end of week two, and the entire amount delivered by the end of week three. Contracts in place with the transportation companies call for at least 45% of the total delivered be delivered by trucking, at least 40% of the total delivered be delivered by railway, and up to 15% of the total delivered be delivered by air cargo. Unfortunately, competing demands limit the availability of each mode of transportation each of the three weeks to the following levels (all in thousands of tons):
Week Trucking Limits Railway Limits Air Cargo Limits 1 45 60 15 2 50 55 10 3 55 45 5 Costs (\ per 1000 tons) \ 200 \ 140 \ 400
The following is the LP model for this logistics problem.

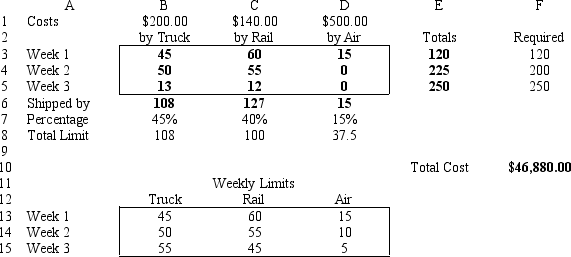 What formula goes in cells F10, E3, E4, E5, and B6 of this Excel spreadsheet?
What formula goes in cells F10, E3, E4, E5, and B6 of this Excel spreadsheet?
(Essay)
4.7/5  (36)
(36)
The hospital administrators at New Hope, County General, and City East recently received notice of an impending state inspection of their facilities. Under new guidelines established to improve the overall health care system, state inspectors will be assessing the efficiency of each hospital. The staff at New Hope has suggested a mutual assistance program in preparation for the inspections and have proposed using DEA as a means to assess the efficiency of each facility. The data collected thus far is summarized in the following table. All data reflects averages compiled over the past six months.
New Hope Countv General City East Input Measures Bed days unused (1000s) 83.0 105.0 104.1 Supply expense (\ 1000) 123.8 162.3 154.0 Full-time staff 225.0 200.0 231.0 Output Measures Patient-days (1000s) 105.0 71.0 82.7 Nurses qualified 253.0 92.0 175.0 Assistants on staff 125.0 45.0 65.0 Custnmer satisfactinn 98.0 88.0 83.0
Enter the numbers in the appropriate cells of ranges B4:H6 in the Excel spreadsheet to solve this problem based on the following formulation.
Let werght as5igned to dutput
waight as5igned to ingut
MAX:
Subject to:
![The hospital administrators at New Hope, County General, and City East recently received notice of an impending state inspection of their facilities. Under new guidelines established to improve the overall health care system, state inspectors will be assessing the efficiency of each hospital. The staff at New Hope has suggested a mutual assistance program in preparation for the inspections and have proposed using DEA as a means to assess the efficiency of each facility. The data collected thus far is summarized in the following table. All data reflects averages compiled over the past six months. \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \text { Hospital } \begin{array}{lccc} &\text { New Hope } & \text { Countv General } & \text { City East }\\ \hline \text { Input Measures } & & & \\ \text { Bed days unused (1000s) } & 83.0 & 105.0 & 104.1 \\ \text { Supply expense }(\$ 1000 \mathrm{~s}) & 123.8 & 162.3 & 154.0 \\ \text { Full-time staff } & 225.0 & 200.0 & 231.0 \\ \text { Output Measures } & & & \\ \text { Patient-days (1000s) } & 105.0 & 71.0 & 82.7 \\ \text { Nurses qualified } & 253.0 & 92.0 & 175.0 \\ \text { Assistants on staff } & 125.0 & 45.0 & 65.0 \\ \text { Custnmer satisfactinn } & 98.0 & 88.0 & 83.0 \end{array} Enter the numbers in the appropriate cells of ranges B4:H6 in the Excel spreadsheet to solve this problem based on the following formulation. Let \quad w _ { i } = werght as5igned to dutput j , j = 1 , \ldots , 4 \mathbf { v } _ { i } = waight as5igned to ingut i , i = 1 , \ldots , 3 MAX: \left. \left. \quad 82.7 w _ { 1 } + 175 .\right] w _ { 2 } + 65.0 w _ { 3 } + 83 .\right] w _ { 4 } Subject to: 105.1 w _ { 1 } + 253.0 w _ {2 } + 125.0 w _ { 3 } + 98.0 w _ { 4 } - 83.0 v _ { 1 } - 123.8 v _ { 2 } - 225.0 v _ { 3 } \leq 0 71.0 w _ { 1 } + 92.0 w _ { 2 } + 45.0 w _ { 3 } + 88.0 w _ { 4 } - 105.0 v _ { 1 } - 162.3 v _ { 2 } - 200 v _ { 3 } \leq 0 82.7 w _ { 1 } + 175.0 w _ { 2 } + 65.0 w _ { 3 } + 83.0 w _ { 4 } - 104.1 v _ { 1 } - 154.0 v _ { 2 } - 231.0 v _ { 3 } \leq 0 104.1 \mathbf { v } _ { 1 } + 154.0 \mathbf { v } _ { \mathbf { 2 } } + 231.0 \mathbf { v } _ { \mathbf { 3 } } = 1 w _ { 1 , } w _ { 2 } w _ { 3 , } w _ { 4 } , \mathbf { v } _ { 1 } , \mathbf { v } _ { 2 } , \mathbf { v } _ { 3 } \geq0](https://storage.examlex.com/TB2204/11eae782_15fc_1c4c_a367_8329b17844f8_TB2204_00.jpg)
![The hospital administrators at New Hope, County General, and City East recently received notice of an impending state inspection of their facilities. Under new guidelines established to improve the overall health care system, state inspectors will be assessing the efficiency of each hospital. The staff at New Hope has suggested a mutual assistance program in preparation for the inspections and have proposed using DEA as a means to assess the efficiency of each facility. The data collected thus far is summarized in the following table. All data reflects averages compiled over the past six months. \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \text { Hospital } \begin{array}{lccc} &\text { New Hope } & \text { Countv General } & \text { City East }\\ \hline \text { Input Measures } & & & \\ \text { Bed days unused (1000s) } & 83.0 & 105.0 & 104.1 \\ \text { Supply expense }(\$ 1000 \mathrm{~s}) & 123.8 & 162.3 & 154.0 \\ \text { Full-time staff } & 225.0 & 200.0 & 231.0 \\ \text { Output Measures } & & & \\ \text { Patient-days (1000s) } & 105.0 & 71.0 & 82.7 \\ \text { Nurses qualified } & 253.0 & 92.0 & 175.0 \\ \text { Assistants on staff } & 125.0 & 45.0 & 65.0 \\ \text { Custnmer satisfactinn } & 98.0 & 88.0 & 83.0 \end{array} Enter the numbers in the appropriate cells of ranges B4:H6 in the Excel spreadsheet to solve this problem based on the following formulation. Let \quad w _ { i } = werght as5igned to dutput j , j = 1 , \ldots , 4 \mathbf { v } _ { i } = waight as5igned to ingut i , i = 1 , \ldots , 3 MAX: \left. \left. \quad 82.7 w _ { 1 } + 175 .\right] w _ { 2 } + 65.0 w _ { 3 } + 83 .\right] w _ { 4 } Subject to: 105.1 w _ { 1 } + 253.0 w _ {2 } + 125.0 w _ { 3 } + 98.0 w _ { 4 } - 83.0 v _ { 1 } - 123.8 v _ { 2 } - 225.0 v _ { 3 } \leq 0 71.0 w _ { 1 } + 92.0 w _ { 2 } + 45.0 w _ { 3 } + 88.0 w _ { 4 } - 105.0 v _ { 1 } - 162.3 v _ { 2 } - 200 v _ { 3 } \leq 0 82.7 w _ { 1 } + 175.0 w _ { 2 } + 65.0 w _ { 3 } + 83.0 w _ { 4 } - 104.1 v _ { 1 } - 154.0 v _ { 2 } - 231.0 v _ { 3 } \leq 0 104.1 \mathbf { v } _ { 1 } + 154.0 \mathbf { v } _ { \mathbf { 2 } } + 231.0 \mathbf { v } _ { \mathbf { 3 } } = 1 w _ { 1 , } w _ { 2 } w _ { 3 , } w _ { 4 } , \mathbf { v } _ { 1 } , \mathbf { v } _ { 2 } , \mathbf { v } _ { 3 } \geq0](https://storage.examlex.com/TB2204/11eae782_15fc_1c4d_a367_edbfdc9597d0_TB2204_00.jpg)
(Essay)
4.9/5  (41)
(41)
Models which are setup in an intuitively appealing, logical layout tend to be the most
(Multiple Choice)
4.8/5  (36)
(36)
Showing 21 - 40 of 88
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)