Question 1

The allowable increase for a changing cell (decision variable) is

Accepted Answer

A)  how many more units to produce to maximize profits. 
B)  the amount by which the objective function coefficient can increase without changing the optimal solution. 
C)  how much to charge to get the optimal solution. 
D)  the amount by which constraint coefficient can increase without changing the optimal solution. 
A)  how many more units to produce to maximize profits. 
B)  the amount by which the objective function coefficient can increase without changing the optimal solution. 
C)  how much to charge to get the optimal solution. 
D)  the amount by which constraint coefficient can increase without changing the optimal solution.

Question 2

Why might a decision maker prefer a solution in the interior of the feasible region of a linear programming problem?

Accepted Answer

A)  Such a solution has a better objective function value than any other solution 
B)  Such a solution is likely to remain feasible if some of the coefficients in the problem change 
C)  The decision maker is not sure if he/she wants to maximize or minimize the objective 
D)  Such a solution has more binding constraints 
A)  Such a solution has a better objective function value than any other solution 
B)  Such a solution is likely to remain feasible if some of the coefficients in the problem change 
C)  The decision maker is not sure if he/she wants to maximize or minimize the objective 
D)  Such a solution has more binding constraints

Question 3

All of the following are true about a variable with a negative reduced cost in a maximization problem except

Accepted Answer

A)  its objective function coefficient must increase by that amount in order to enter the basis. 
B)  it is at its simple lower bound. 
C)  it has surplus resources. 
D)  the objective function value will decrease by that value if the variable is increased by one unit. 
A)  its objective function coefficient must increase by that amount in order to enter the basis. 
B)  it is at its simple lower bound. 
C)  it has surplus resources. 
D)  the objective function value will decrease by that value if the variable is increased by one unit.

Question 4

When a solution is degenerate the shadow prices and their ranges

Accepted Answer

A)  may be interpreted in the usual way but they may not be unique. 
B)  must be disregarded. 
C)  are always valid and unique. 
D)  are always understated 
A)  may be interpreted in the usual way but they may not be unique. 
B)  must be disregarded. 
C)  are always valid and unique. 
D)  are always understated

Question 5

Exhibit 4.1
The following questions are based on the problem below and accompanying Risk Solver Platform (RSP) sensitivity report.
Carlton construction is supplying building materials for a new mall construction project in Kansas. Their contract calls for a total of 250,000 tons of material to be delivered over a three-week period. Carlton's supply depot has access to three modes of transportation: a trucking fleet, railway delivery, and air cargo transport. Their contract calls for 120,000 tons delivered by the end of week one, 80% of the total delivered by the end of week two, and the entire amount delivered by the end of week three. Contracts in place with the transportation companies call for at least 45% of the total delivered be delivered by trucking, at least 40% of the total delivered be delivered by railway, and up to 15% of the total delivered be delivered by air cargo. Unfortunately, competing demands limit the availability of each mode of transportation each of the three weeks to the following levels (all in thousands of tons):
 $$\begin{array} { c c c c } 
\text { Week } & \text { Trucking Lanrits } & \text { Railway Limits } & \text { Air Carga Lavits } \
\hline 1 & 45 & 60 & 15 \
2 & 50 & 55 & 10 \
3 & 55 & 45 & 5 \
\hline \text { Costs } ( \$ \text { per } 1000 \text { tors) } & \$ 200 & \$ 140 & \$ 400
\end{array}$$ The following is the LP model for this logistics problem.
    
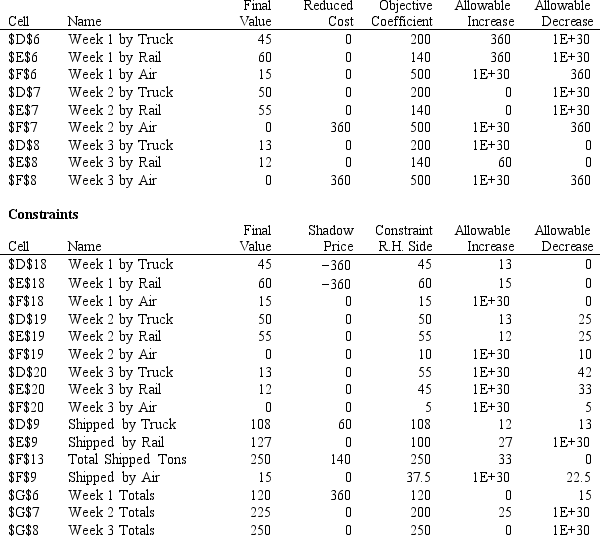-Refer to Exhibit 4.1. Of the three percentage of effort constraints, Shipped by Truck, Shipped by Rail, and Shipped by Air, which should be examined for potential cost reduction?

Accepted Answer

The percentage by Truck, Shipp

Question 6

A farmer is planning his spring planting. He has 20 acres on which he can plant a combination of Corn, Pumpkins and Beans. He wants to maximize his profit but there is a limited demand for each crop. Each crop also requires fertilizer and irrigation water which are in short supply. The following table summarizes the data for the problem.
 $$\begin{array} { l | c c c c c } 
\text { Crap } & \begin{array} { c } 
\text { Profitper } \
\text { Acre ( }
\end{array} & \begin{array} { c } 
\text { Yied per } \
\text { Acre (lb) }
\end{array} & \begin{array} { c } 
\text { Meximum } \
\text { Denand (lb) }
\end{array} & \begin{array} { c } 
\text { Irripation } \
\text { (acreft) }
\end{array} & \begin{array} { c } 
\text { Fetilize } \
\text { (pounds/are) }
\end{array} \
\hline \text { Carm } & 2,100 & 21,000 & 200,000 & 2 & 500 \
\text { pumplin } & 900 & 10,000 & 180,000 & 3 & 400 \
\text { Beans } & 1,050 & 3,500 & 80,000 & 1 & 300
\end{array}$$ Suppose the farmer can purchase more fertilizer for $2.50 per pound, should he purchase it and how much can he buy and still be sure of the value of the additional fertilizer? Base your response on the following Risk Solver Platform (RSP) sensitivity output.
 $\text { Changing Cells}$
$\begin{array}{llrrrrr}
&&\text { Final } & \text { Reduced } & \text { Objective } & \text { Allowable } & \text { Allowable }\
\text { Cell } & \text { Name } & \text { Value } & \text { Cost } & \text { Coefficient } & \text { Increase } & \text { Decrease } \
\hline \$ B \$ 4 & \text { Acres of Corn } & 9.52 & 0 & 2100 & 1 \mathrm{E}+30 & 350 \
\$ \mathrm{C} \$ 4 & \text { Acres of Pumpkin } & 0 & -500.01 & 899.99 & 500.01 & 1 \mathrm{E}+30 \
\$ \mathrm{D} \$ 4 & \text { Acres of Beans } & 10.79 & 0 & 1050 & 210 & 375.00
\end{array}$

$\text { Constraints }$
$\begin{array}{llrrrrr}
&&\text { Final } & \text {Shadow } & \text {Constraint } & \text {Allowable } & \text {Allowable }\
\text { Cell } & \text { Name } & \text { Value } & \text { Price } & \text { R.H. Side } & \text { Increase } & \text { Decrease } \
\hline \$ \mathrm{E} \$ 8 & \text { Corn demand Used } & 200000 & 0.017 & 200000 & 136000 & 152000 \
\$ \mathrm{E} \$ 9 & \text { Pumpkin demand Used } & 0 & 0 & 180000 & 1 \mathrm{E}+30 & 180000 \
\$ \mathrm{E} \$ 10 & \text { Bean demand Used } & 37777.78 & 0 & 80000 & 1 \mathrm{E}+30 & 42222.22 \
\$ \mathrm{E} \$ 11 & \text { Water Used } & 29.84 & 0 & 50 & 1 \mathrm{E}+30 & 20.15 \
\$ \mathrm{~F} \$ 12 & \text { Fertilizer Userl } & 8000 & 35 & 8000 & 3610 ก 4 & 323800
\end{array}$

Accepted Answer

Yes, because the cost of $2.50

Question 7

The coefficients in an LP model (cj, aij, bj) represent

Accepted Answer

A)  random variables. 
B)  numeric constants. 
C)  random constants. 
D)  numeric variables. 
A)  random variables. 
B)  numeric constants. 
C)  random constants. 
D)  numeric variables.

Question 8

The absolute value of the shadow price indicates the amount by which the objective function will be

Accepted Answer

A)  improved if the corresponding constraint is loosened. 
B)  improved if the corresponding constraint is tightened. 
C)  made worse if the corresponding constraint is loosened. 
D)  improved if the corresponding constraint is unchanged. 
A)  improved if the corresponding constraint is loosened. 
B)  improved if the corresponding constraint is tightened. 
C)  made worse if the corresponding constraint is loosened. 
D)  improved if the corresponding constraint is unchanged.

Question 9

The slope of the level curve for the objective function value can be changed by

Accepted Answer

A)  increasing the value of the decision variables. 
B)  doubling all the coefficients in the objective function. 
C)  increasing the right hand sides of constraints. 
D)  changing a coefficient in the objective function. 
A)  increasing the value of the decision variables. 
B)  doubling all the coefficients in the objective function. 
C)  increasing the right hand sides of constraints. 
D)  changing a coefficient in the objective function.

Question 10

Risk Solver Platform (RSP) provides sensitivity analysis information on all of the following except the

Accepted Answer

A)  range of values for objective function coefficients which do not change optimal solution. 
B)  impact on optimal objective function value of changes in constrained resources. 
C)  impact on optimal objective function value of changes in value of decision variables. 
D)  impact on right hand sides of changes in constraint coefficients. 
A)  range of values for objective function coefficients which do not change optimal solution. 
B)  impact on optimal objective function value of changes in constrained resources. 
C)  impact on optimal objective function value of changes in value of decision variables. 
D)  impact on right hand sides of changes in constraint coefficients.

Question 11

The Simplex method uses which of the following values to determine if the objective function value can be improved?

Accepted Answer

A)  shadow price 
B)  target value 
C)  reduced cost 
D)  basic cost 
A)  shadow price 
B)  target value 
C)  reduced cost 
D)  basic cost

Question 12

Jones Furniture Company produces beds and desks for college students. The production process requires carpentry and varnishing. Each bed requires 6 hours of carpentry and 4 hour of varnishing. Each desk requires 4 hours of carpentry and 8 hours of varnishing. There are 36 hours of carpentry time and 40 hours of varnishing time available. Beds generate $30 of profit and desks generate $40 of profit. Demand for desks is limited so at most 8 will be produced.
Suppose the company can purchase more varnishing time for $3.00, should it be purchased and how much can be bought before the value of the additional time is uncertain? Base your response on the following Risk Solver Platform (RSP) sensitivity output.
 Laet
$$\begin{array} { l } 
X _ { 1 } = \text { Number of Beds to produce } \
X _ { \mathbf { 2 } } = \text { Number of Desks to produce }
\end{array}$$ The LP model for the problem is
 $\text { MAX: } \quad 30 \mathrm{X}_{1}+40 \mathrm{X}_{2}$
$\begin{array}{l}
\text { Subject to: }\
\begin{array} { l } 
6 X _ { 1 } + 4 X _ { 2 } \leq 36 \text { (carpentry) } \
4 X _ { 1 } + \mathbf { 8 } X _ { 2 } \leq 40 \text { (varnishing } \
X _ { 2 } \leq \mathbf { 8 } \left( \text { demand for } X _ { 2 } \right) \
X _ { 1 } , X _ { 2 } \geq 0
\end{array}
\end{array}$ $\text { Changing Cells}$
$\begin{array}{llrrrrr}
&&\text { Final } & \text { Reduced } & \text { Objective } & \text { Allowable } & \text { Allowable }\
\text { Cell } & \text { Name } & \text { Value } & \text { Cost } & \text { Coefficient } & \text { Increase } & \text { Decrease } \
\hline \$ \mathrm{~B} \$ 4 & \text { Number to make: Beds } & 4 & 0 & 30 & 30 & 10 \
\$ \mathrm{C} \$ 4 & \text { Number to make: Desks } & 3 & 0 & 40 & 20 & 20
\end{array}$

$\text { Constraints }$
$\begin{array}{llrrrrr}
&&\text { Final } & \text {Shadow } & \text {Constraint } & \text {Allowable } & \text {Allowable }\
\text { Cell } & \text { Name } & \text { Value } & \text { Price } & \text { R.H. Side } & \text { Increase } & \text { Decrease } \ 
\hline\$ \mathrm{D} \$ 8 & \text { Carpentry Used } & 36 & 2.5 & 36 & 24 & 16 \
\$ \mathrm{D} \$ 9 & \text { Varnishing Used } & 40 & 3.75 & 40 & 26.67 & 16 \
\$ \mathrm{D} \$ 10 & \text { Desk demand Used } & 3 & 0 & 8 & 1 \mathrm{E}+30 & 5
\end{array}$

Accepted Answer

Yes, because the cost of $3.00

Question 13

What is the value of the slack variable in the following constraint when X1 and X2 are nonbasic and only non-negativity is used as simple bounds? X1 + X2 + S1 = 100

Accepted Answer

A)  0 
B)  50 
C)  100 
D)  can't be determined from the given information 
A)  0 
B)  50 
C)  100 
D)  can't be determined from the given information

Question 14

Exhibit 4.2
The following questions correspond to the problem below and associated Risk Solver Platform (RSP) sensitivity report.
Robert Hope received a welcome surprise in this management science class; the instructor has decided to let each person define the percentage contribution to their grade for each of the graded instruments used in the class. These instruments were: homework, an individual project, a mid-term exam, and a final exam. Robert's grades on these instruments were 75, 94, 85, and 92, respectively. However, the instructor complicated Robert's task somewhat by adding the following stipulations:
 -homewark can account far up to $25 \%$ of the grade, but must be at least $5 \%$ af the grade;
- the praject can account for up to $25 \%$ of the grade, but must be at least $5 \%$ af the grade;
- the mid-term and final must each accaunt far betwen $10 \%$ and $40 \%$ of the grade but cannot accaunt far mare than $7 \%$ of the grade when the percentages are cambined; and 
-the project and final exam grades may not collectively constitute more than $50 \%$ of the Iratade. The following LP model allows Robert to maximize his numerical grade.
 $$\begin{array} { l } 
\text { Let } \quad W _ { 1 } = \text { weight as51gMed to hamewark } \
W _ { \mathbf { 2 } } = \text { waight as5igned to the praject } \
W _ { 3 } = \text { weight assigned to the midi-term } \
W _ { 4 } = \text { waight as5igned to the final } \\
\text { MAX: } \quad 75 \mathrm {~W} _ { 1 } + 94 \mathrm {~W} _ { 2 } + 85 \mathrm {~W} _ { 3 } + 92 \mathrm {~W} _ { 4 } \
\text { Subject ta: } \quad W _ { 1 } + W _ { 2 } + W _ { 3 } + W _ { 4 } = 1 \
W _ { 3 } + W _ { 4 } \leq 0.70 \
W _ { 3 } + W _ { 4 } \geq 0.50 \
\text { 0. } 05 \leq W _ { 1 } \leq 0.25 \
\text { 0. } 05 \leq W _ { 2 } \leq 0.25 \
\text { 0.10 } \leq W _ { 3 } \leq 0 .4 0 \
0 .10 \leq W _ { 4 } \leq 0.40 \
\end{array}$$ $\text { Adjustaibla Calls}$

$\begin{array}{llrrrrr}
&&\text { Final } & \text { Reduced } & \text { Objective} & \text {  Allowable } & \text { Allowable }\
\text { Cell } & \text { Name } & \text { Value } & \text { Cost  } & \text {Coefficient  } & \text {Increase } & \text { Decrease }\
\hline \$ F \$ 5 & \text { Mid Term to grade } & 0.40 & 10.00 & 85 & 1 \mathrm{E}+30 & 10 \
\$ F \$ 6 & \text { Final to grade } & 0.25 & 0.00 & 92 & 2 & 17 \
\$ F \$ 7 & \text { Project to grade } & 0.25 & 2.00 & 94 & 1 \mathrm{E}+30 & 2 \
\$ F \$ 8 & \text { Homework to grade } & 0.10 & 0.00 & 75 & 10 & 1 \mathrm{E}+30
\end{array}$

$\text { Constraints }$ 
$\begin{array}{llrrrrrr}
&&\text { Final } & \text { Shadow  } & \text { Constraint} & \text {  Allowable } & \text { Allowable }\
\text { Cell } & \text { Name } & \text { Value } & \text { Price } & \text { R.H. Side } & \text { Increase } & \text { Decrease } \
\hline \$ E \$ 14 & \text { Both Exams Total } & 0.65 & 0 & 0.7 & 1 \mathrm{E}+30 & 0.05 \
\$ E \$ 15 & \text { Final \& Project Total } & 0.5 & 17 & 0.5 & 0.05 & 0.15 \
\$ F \$ 9 & 100 \% \text { to gracle } & 1.00 & 75.00 & 1 & 0.15 & 0.05
\end{array}$
-Refer to Exhibit 4.2. Based on the Risk Solver Platform (RSP) sensitivity report information, is there anything Robert can request of his instructor to improve his final grade?

Accepted Answer

Robert can request an increase

Question 15

What is the value of the objective function if X1 is set to 0 in the following Limits Report? $\begin{array}{llc}
&\text { Target }\
\text { Cell } & \text { Name } & \text { Value } \
\hline \$ \mathrm{E} \$ 5 & \text { Unit profit: Total Profit: } & 3200
\end{array}$

$\begin{array}{llrrrrr}
&\text {Adiustable}&&\text {Lower }&\text {Target }&\text {Upper}&\text { Targel}\
\text { Cell } & \text { Name } & \text { Value } & \text { Limit } & \text { Result } & \text { Limit } & \text { Result } \
\hline \$ \text { B } \$ 4 & \text { Number to make: } \mathrm{X} 1 & 80 & 0 & 800 & 79.9999999 & 3200 \
\$ \text { C } \$ 4 & \text { Number to make } \mathrm{X} 2 & 20 & 0 & 24 & 20 & 3200
\end{array}$

Accepted Answer

A)  80 
B)  800 
C)  2400 
D)  3200 
A)  80 
B)  800 
C)  2400 
D)  3200

Question 16

Identify the different sets of basic variables that might be used to obtain a solution to this problem.
 MIN: $\quad 2.5 \mathbf { X } _ { 1 } + 1.5 \mathbf { X } _ { \mathbf { 2 } }$
Subject to:
$$\begin{array} { l } 
4 X _ { 1 } + 3 X _ { 2 } \geq 24 \
2 X _ { 1 } + 4 X _ { 2 } \geq 24 \
X _ { 1 } ,X _ { 2 } \geq 0
\end{array}$$

Accepted Answer

The answer of Identify the different sets of basic variables...

Question 17

Benefits of sensitivity analysis include all the following except:

Accepted Answer

A)  provides a better picture of how solutions change as model factors change. 
B)  fosters managerial acceptance of the optimal solution. 
C)  overcomes management skepticism of optimal solutions. 
D)  answers potential managerial questions regarding the solution to an LP problem. 
A)  provides a better picture of how solutions change as model factors change. 
B)  fosters managerial acceptance of the optimal solution. 
C)  overcomes management skepticism of optimal solutions. 
D)  answers potential managerial questions regarding the solution to an LP problem.

Question 18

Given the following Risk Solver Platform (RSP) sensitivity output what range of values can the objective function coefficient for variable X1 assume without changing the optimal solution?
 $\text {Changing Calls}$
$\begin{array}{llrrrrr}
&&\text { Final} &\text {Reduced }&\text {Objective }&\text {Allowable}&\text { Allowable }\
\text { Cell } & \text { Name } & \text { Value } & \text { Cost } & \text { Coefficient } & \text { Increase } & \text { Decrease } \
\hline \$ \mathrm{~B} \$ 4 & \text { Number to make: } \mathrm{X} 1 & 9.49 & 0 & 5 & 1.54 & 1 \
\$ \mathrm{C} \$ 4 & \text { Number to make: } \mathrm{X} 2 & 1.74 & 0 & 6 & 1.5 & 1.47
\end{array}$

$\text {Constraints}$
$\begin{array}{llrrrrr}
&&\text { Final } &\text {Shadow} &\text { Constraint } &\text {Allowable} &\text { Allowable }\
\text { Cell } & \text { Name } & \text { Value } & \text { Price } & \text { R.H. Side } & \text { Increase } & \text { Decrease } \
\hline \$ \mathrm{D} \$ 8 & \text { Used } & 42 & 0 & 48 & 1 \mathrm{E}+30 & 6 \
\$ \mathrm{D} \$ 9 & \text { Used } & 132 & 0.24 & 132 & 12 & 12 \
\$ \mathrm{D} \$ 10 & \text { Used } & 24 & 124 & 24 & 133 & 2
\end{array}$

Accepted Answer

The answer of Given the following Risk Solver Platform (RSP)...

Question 19

When automatically running multiple optimizations in Risk Solver Platform (RSP), what spreadsheet function indicates which optimization is being run?

Accepted Answer

A)  =PsiOptNum() 
B)  =PsiOptValue() 
C)  =PsiOptIndex() 
D)  =PsiCurrentOpt() 
A)  =PsiOptNum() 
B)  =PsiOptValue() 
C)  =PsiOptIndex() 
D)  =PsiCurrentOpt()

Question 20

Meaningful Risk Solver Platform (RSP) sensitivity report headings can be defined

Accepted Answer

A)  by adding cell notes to spreadsheet cells. 
B)  by using the Guess button in the Risk Solver Platform (RSP) dialog box. 
C)  by carefully labeling rows and columns in the spreadsheet model. 
D)  naming cells in the spreadsheet model. 
A)  by adding cell notes to spreadsheet cells. 
B)  by using the Guess button in the Risk Solver Platform (RSP) dialog box. 
C)  by carefully labeling rows and columns in the spreadsheet model. 
D)  naming cells in the spreadsheet model.

The allowable increase for a changing cell (decision variable) is

Why might a decision maker prefer a solution in the interior of the feasible region of a linear programming problem?

All of the following are true about a variable with a negative reduced cost in a maximization problem except

When a solution is degenerate the shadow prices and their ranges

The coefficients in an LP model (c_j, a_ij, b_j) represent

The absolute value of the shadow price indicates the amount by which the objective function will be

The slope of the level curve for the objective function value can be changed by

Risk Solver Platform (RSP) provides sensitivity analysis information on all of the following except the

The Simplex method uses which of the following values to determine if the objective function value can be improved?

What is the value of the slack variable in the following constraint when X₁ and X₂ are nonbasic and only non-negativity is used as simple bounds? X₁+ X₂ + S₁ = 100

Identify the different sets of basic variables that might be used to obtain a solution to this problem. MIN: $\quad 2.5 \mathbf { X } _ { 1 } + 1.5 \mathbf { X } _ { \mathbf { 2 } }$ Subject to: 4+3\geq24 2+4\geq24 ,\geq0

Benefits of sensitivity analysis include all the following except:

When automatically running multiple optimizations in Risk Solver Platform (RSP), what spreadsheet function indicates which optimization is being run?

Meaningful Risk Solver Platform (RSP) sensitivity report headings can be defined

Introduction to Modeling and Decision Analysis

Introduction to Optimization and Linear Programming

Modeling and Solving Lp Problems in a Spreadsheet

Network Modeling

Integer Linear Programming

Goal Programming and Multiple Objective Optimization

Nonlinear Programming and Evolutionary Optimization

Regression Analysis

Discriminant Analysis

Time Series Forecasting

Introduction to Simulation Using Risk Solver Platform

Queuing Theory

Decision Analysis

Project Management Online

Filters

Exam 4: Sensitivity Analysis and the Simplex Method

The allowable increase for a changing cell (decision variable) is

Why might a decision maker prefer a solution in the interior of the feasible region of a linear programming problem?

All of the following are true about a variable with a negative reduced cost in a maximization problem except

When a solution is degenerate the shadow prices and their ranges

The coefficients in an LP model (cj, aij, bj) represent

The absolute value of the shadow price indicates the amount by which the objective function will be

The slope of the level curve for the objective function value can be changed by

Risk Solver Platform (RSP) provides sensitivity analysis information on all of the following except the

The Simplex method uses which of the following values to determine if the objective function value can be improved?

What is the value of the slack variable in the following constraint when X1 and X2 are nonbasic and only non-negativity is used as simple bounds? X1 + X2 + S1 = 100

Identify the different sets of basic variables that might be used to obtain a solution to this problem. MIN: 2.5X1+1.5X2\quad 2.5 \mathbf { X } _ { 1 } + 1.5 \mathbf { X } _ { \mathbf { 2 } }2.5X1​+1.5X2​ Subject to: 4+3\geq24 2+4\geq24 ,\geq0

Benefits of sensitivity analysis include all the following except:

When automatically running multiple optimizations in Risk Solver Platform (RSP), what spreadsheet function indicates which optimization is being run?

Meaningful Risk Solver Platform (RSP) sensitivity report headings can be defined

Introduction to Modeling and Decision Analysis

Introduction to Optimization and Linear Programming

Modeling and Solving Lp Problems in a Spreadsheet

Network Modeling

Integer Linear Programming

Goal Programming and Multiple Objective Optimization

Nonlinear Programming and Evolutionary Optimization

Regression Analysis

Discriminant Analysis

Time Series Forecasting

Introduction to Simulation Using Risk Solver Platform

Queuing Theory

Decision Analysis

Project Management Online

Filters

The coefficients in an LP model (c_j, a_ij, b_j) represent

What is the value of the slack variable in the following constraint when X₁ and X₂ are nonbasic and only non-negativity is used as simple bounds? X₁+ X₂ + S₁ = 100

Identify the different sets of basic variables that might be used to obtain a solution to this problem. MIN: $\quad 2.5 \mathbf { X } _ { 1 } + 1.5 \mathbf { X } _ { \mathbf { 2 } }$ Subject to: 4+3\geq24 2+4\geq24 ,\geq0