Question 1

The reduced cost for a changing cell (decision variable) is

Accepted Answer

A)  the amount by which the objective function value changes if the variable is increased by one unit. 
B)  how many more units to product to maximize profits. 
C)  the per unit profits minus the per unit costs for that variable. 
D)  equal to zero for variables at their optimal values. 
A)  the amount by which the objective function value changes if the variable is increased by one unit. 
B)  how many more units to product to maximize profits. 
C)  the per unit profits minus the per unit costs for that variable. 
D)  equal to zero for variables at their optimal values.

Question 2

Given the following Risk Solver Platform (RSP) sensitivity output how much does the objective function coefficient for X2 have to increase before it enters the optimal solution at a strictly positive value?
 $\begin{array}{llrrrrr}
&&\text { Final} & \text {  Reduced } & \text { Objective } & \text { Allowable } & \text { Allowable }\
\text { Cell } & \text { Name } & \text { Value } & \text { Cost } & \text { Coefficient } & \text { Increase } & \text { Decrease } \
\hline \$ \mathrm{~B} \$ 4 & \mathrm{X} 1 & 9.52 & 0 & 2100 & 1 \mathrm{E}+30 & 350 \
\$ \mathrm{C} \$ 4 & \mathrm{X} 2 & 0 & -500.01 & 899.99 & 500.01 & 1 \mathrm{E}+30 \
\$ \mathrm{D} \$ 4 & \mathrm{X} 3 & 1079 & 0 & 1050 & 210 & 37501
\end{array}$

Accepted Answer

Question 3

A binding greater than or equal to ($\ge$) constraint in a minimization problem means that

Accepted Answer

A)  the variable is up against an upper limit. 
B)  the minimum requirement for the constraint has just been met. 
C)  another constraint is limiting the solution. 
D)  the shadow price for the constraint will be positive. 
A)  the variable is up against an upper limit. 
B)  the minimum requirement for the constraint has just been met. 
C)  another constraint is limiting the solution. 
D)  the shadow price for the constraint will be positive.

Question 4

Consider the following linear programming model and Risk Solver Platform (RSP) sensitivity output. What is the optimal objective function value if the RHS of the first constraint increases to 18?
 $$\begin{array} { l l } 
\operatorname { MAX } : & 7 \mathbf { X } _ { 1 } + 4 \mathbf { X } _ { \mathbf { 2 } } \
\text { Subject ta: } & 2 \mathbf { X } _ { 1 } + \mathbf { X } _ { \mathbf { 2 } } \leq 10 \
& \mathbf { X } _ { 1 } + \mathbf { X } _ { \mathbf { 2 } } \leq 10 \
& 2 \mathbf { X } _ { 1 } + 5 \mathbf { X } _ { \mathbf { 2 } } \leq 40 \
& \mathbf { X } _ { 1 } \mathbf { X } _ { \mathbf { 2 } } \geq \mathbf { 0 }\

\end{array}$$ $\text {Changing Calls}$
$\begin{array}{llrrrrr}
&&\text { Final} &\text {Reduced }&\text {Objective }&\text {Allowable}&\text { Allowable }\
\text { Cell } & \text { Name } & \text { Value } & \text { Cost } & \text { Coefficient } & \text { Increase } & \text { Decrease } \
\hline \$ \mathrm{~B} \$ 4 & \text { Number to make: } \mathrm{X} 1 &6& 0 & 7& 1& 3\
\$ \mathrm{C} \$ 4 & \text { Number to make: } \mathrm{X} 2 & 4 & 0 &4 &3 & 0.5\

\end{array}$

$\text {Constraints}$
$\begin{array}{llrrrrr}
&&\text { Final } &\text {Shadow} &\text { Constraint } &\text {Allowable} &\text { Allowable }\
\text { Cell } & \text { Name } & \text { Value } & \text { Price } & \text { R.H. Side } & \text { Increase } & \text { Decrease } \
\hline \$ \mathrm{D} \$ 8 & \text { Used } & 16&3 & 16&4&2.67 \
\$ \mathrm{D} \$ 9 & \text { Used } & 10 & 1&10 & 1 & 2 \
\$ \mathrm{D} \$ 10 & \text { Used } & 32& 0 & 40 & 1 E+30 & 8
\end{array}$

Accepted Answer

Shadow price of first constrai

Question 5

How many basic variables are there in a linear programming model which has n variables and m constraints?

Accepted Answer

A)  n 
B)  m 
C)  n + m 
D)  n- m 
A)  n 
B)  m 
C)  n + m 
D)  n- m

Question 6

Is the optimal solution to this problem unique, or is there an alternate optimal solution? Explain your reasoning.
 $\mathrm { MAX } \quad 5 \mathrm { X } _ { 1 } + 2 \mathrm { X } _ { 2 }$
Subject ta:
$\begin{array} { l } 
3 X _ { 1 } + 5 X _ { \mathbf { 2} } \leq 15 \
10 X _ { 1 } + 4 X _ { \mathbf { 2 } } \leq 20 \
X _ { 1 } , X _ { 2 } \geq 0
\end{array}$ $\text {Changing Calls}$
$\begin{array}{llrrrrr}
&&\text { Final} &\text {Reduced }&\text {Objective }&\text {Allowable}&\text { Allowable }\
\text { Cell } & \text { Name } & \text { Value } & \text { Cost } & \text { Coefficient } & \text { Increase } & \text { Decrease } \
\hline \$ \mathrm{~B} \$ 4 & \text { Number to make: } \mathrm{X} 1 &2& 0 & 5& 1E+30& 0 \
\$ \mathrm{C} \$ 4 & \text { Number to make: } \mathrm{X} 2 & 0 & 0 & 2 &0 & 1E+30
\end{array}$

$\text {Constraints}$
$\begin{array}{llrrrrr}
&&\text { Final } &\text {Shadow} &\text { Constraint } &\text {Allowable} &\text { Allowable }\
\text { Cell } & \text { Name } & \text { Value } & \text { Price } & \text { R.H. Side } & \text { Increase } & \text { Decrease } \
\hline \$ \mathrm{D} \$ 8 & \text { Used } & 6&0 & 15 & 1E+30 &9 \
\$ \mathrm{D} \$ 9 & \text { Used } & 20 & 0.5 & 20 & 30 & 20 \
\end{array}$

Accepted Answer

Alternate optimal solutions ex

Question 7

What is the smallest value of the objective function coefficient X1 can assume without changing the optimal solution?
 $$\begin{array} { l l } 
\operatorname { MAX } : & 7 \mathbf { X } _ { 1 } + 4 \mathbf { X } _ { \mathbf { 2 } } \
\text { Subject ta: } & 2 \mathbf { X } _ { 1 } + \mathbf { X } _ { \mathbf { 2 } } \leq 16 \
& \mathbf { X } _ { 1 } + \mathbf { X } _ { \mathbf { 2 } } \leq 10 \
& 2 \mathbf { X } _ { 1 } + 5 \mathbf { X } _ { \mathbf { 2 } } \leq 40 \
& \mathbf { X } _ { 1 } \mathbf { X } _ { \mathbf { 2 } } \geq \mathbf {0 }
\end{array}$$ $\text {Changing Calls}$
$\begin{array}{llrrrrr}
&&\text { Final} &\text {Reduced }&\text {Objective }&\text {Allowable}&\text { Allowable }\
\text { Cell } & \text { Name } & \text { Value } & \text { Cost } & \text { Coefficient } & \text { Increase } & \text { Decrease } \
\hline \$ \mathrm{~B} \$ 4 & \text { Number to make: } \mathrm{X} 1 &6& 0 & 7& 1& 3\
\$ \mathrm{C} \$ 4 & \text { Number to make: } \mathrm{X} 2 & 4 & 0 &4 &3 & 0.5\

\end{array}$

$\text {Constraints}$
$\begin{array}{llrrrrr}
&&\text { Final } &\text {Shadow} &\text { Constraint } &\text {Allowable} &\text { Allowable }\
\text { Cell } & \text { Name } & \text { Value } & \text { Price } & \text { R.H. Side } & \text { Increase } & \text { Decrease } \
\hline \$ \mathrm{D} \$ 8 & \text { Used } & 16&3 & 16&4&2.67 \
\$ \mathrm{D} \$ 9 & \text { Used } & 10 & 1&10 & 1 & 2 \
\$ \mathrm{D} \$ 10 & \text { Used } & 32& 0 & 40 & 1 E+30 & 8
\end{array}$

Accepted Answer

Coefficien

Question 8

Identify the different sets of basic variables that might be used to obtain a solution to this problem.
 $\mathrm { MAX } : \quad \mathbf { 8 \mathbf { X } _ { 1 } } + 4 \mathbf { X } _ { \mathbf { 2 } }$
Subject to:
$\begin{array} { l } 
5 \mathbf { X } _ { 1 } + 5 \mathbf { X } _ { 2 } \leq 20 \
6 \mathbf { X } _ { 1 } + 2 \mathbf { X } _ { 2 } \leq 18 \
\mathbf { X } _ { 1 } , \mathbf { X } _ { \mathbf { 2 } } \geq 0
\end{array}$

Accepted Answer

The answer of Identify the different sets of basic variables...

Question 9

Exhibit 4.1
The following questions are based on the problem below and accompanying Risk Solver Platform (RSP) sensitivity report.
Carlton construction is supplying building materials for a new mall construction project in Kansas. Their contract calls for a total of 250,000 tons of material to be delivered over a three-week period. Carlton's supply depot has access to three modes of transportation: a trucking fleet, railway delivery, and air cargo transport. Their contract calls for 120,000 tons delivered by the end of week one, 80% of the total delivered by the end of week two, and the entire amount delivered by the end of week three. Contracts in place with the transportation companies call for at least 45% of the total delivered be delivered by trucking, at least 40% of the total delivered be delivered by railway, and up to 15% of the total delivered be delivered by air cargo. Unfortunately, competing demands limit the availability of each mode of transportation each of the three weeks to the following levels (all in thousands of tons):
 $$\begin{array} { c c c c } 
\text { Week } & \text { Trucking Lanrits } & \text { Railway Limits } & \text { Air Carga Lavits } \
\hline 1 & 45 & 60 & 15 \
2 & 50 & 55 & 10 \
3 & 55 & 45 & 5 \
\hline \text { Costs } ( \$ \text { per } 1000 \text { tors) } & \$ 200 & \$ 140 & \$ 400
\end{array}$$ The following is the LP model for this logistics problem.
    
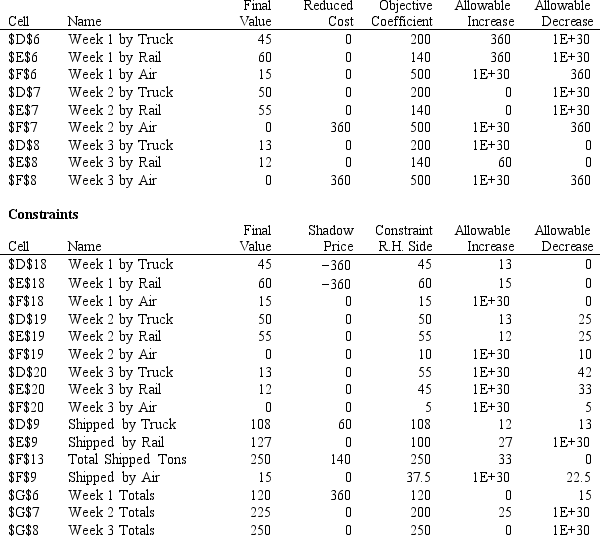-Refer to Exhibit 4.1. Are there alternate optimal solutions to this problem?

Accepted Answer

Cannot tell because we cannot rule out d

Question 10

Binding constraints have

Accepted Answer

A)  zero slack. 
B)  negative slack. 
C)  positive slack. 
D)  surplus resources. 
A)  zero slack. 
B)  negative slack. 
C)  positive slack. 
D)  surplus resources.

Question 11

The allowable decrease for a constraint is

Accepted Answer

A)  how many more units of resource to purchase to maximize profits. 
B)  the amount by which the resource can decrease given shadow price. 
C)  how much resource to use to get the optimal solution. 
D)  the amount by which constraint coefficient can increase without changing the final optimal value. 
A)  how many more units of resource to purchase to maximize profits. 
B)  the amount by which the resource can decrease given shadow price. 
C)  how much resource to use to get the optimal solution. 
D)  the amount by which constraint coefficient can increase without changing the final optimal value.

Question 12

What is the optimal objective function value if X1 is at its lower limit in the following Risk Solver Platform (RSP) sensitivity output?
 $\begin{array}{llc}
&\text { Target }\
\text { Cell } & \text { Name } & \text { Value } \
\hline \$ \mathrm{E} \$ 5 & \text {  Unit profit: OBJ. FN. VALUE  } & 58
\end{array}$

$\begin{array}{llrrrrr}
&\text {Adiustable}&&\text {Lower }&\text {Target }&\text {Upper}&\text { Targel}\
\text { Cell } & \text { Name } & \text { Value } & \text { Limit } & \text { Result } & \text { Limit } & \text { Result } \
\hline \$ \text { B } \$ 4 & \text { Number to make: } \mathrm{X} 1 & 6 & 0 &16 & 6& 58\
\$ \text { C } \$ 4 & \text { Number to make } \mathrm{X} 2 & 4 & 6 & 42 & 4 & 58
\end{array}$

Accepted Answer

The reduced cost for a changing cell (decision variable) is

A binding greater than or equal to ( $\ge$ ) constraint in a minimization problem means that

How many basic variables are there in a linear programming model which has n variables and m constraints?

Identify the different sets of basic variables that might be used to obtain a solution to this problem. $\mathrm { MAX } : \quad \mathbf { 8 \mathbf { X } _ { 1 } } + 4 \mathbf { X } _ { \mathbf { 2 } }$ Subject to: 5+5\leq20 6+2\leq18 ,\geq0

Binding constraints have

The allowable decrease for a constraint is

Introduction to Modeling and Decision Analysis

Introduction to Optimization and Linear Programming

Modeling and Solving Lp Problems in a Spreadsheet

Network Modeling

Integer Linear Programming

Goal Programming and Multiple Objective Optimization

Nonlinear Programming and Evolutionary Optimization

Regression Analysis

Discriminant Analysis

Time Series Forecasting

Introduction to Simulation Using Risk Solver Platform

Queuing Theory

Decision Analysis

Project Management Online

Filters

Exam 4: Sensitivity Analysis and the Simplex Method

The reduced cost for a changing cell (decision variable) is

A binding greater than or equal to ( ≥\ge≥ ) constraint in a minimization problem means that

How many basic variables are there in a linear programming model which has n variables and m constraints?

Identify the different sets of basic variables that might be used to obtain a solution to this problem. MAX:8X1+4X2\mathrm { MAX } : \quad \mathbf { 8 \mathbf { X } _ { 1 } } + 4 \mathbf { X } _ { \mathbf { 2 } }MAX:8X1​+4X2​ Subject to: 5+5\leq20 6+2\leq18 ,\geq0

Binding constraints have

The allowable decrease for a constraint is

Introduction to Modeling and Decision Analysis

Introduction to Optimization and Linear Programming

Modeling and Solving Lp Problems in a Spreadsheet

Network Modeling

Integer Linear Programming

Goal Programming and Multiple Objective Optimization

Nonlinear Programming and Evolutionary Optimization

Regression Analysis

Discriminant Analysis

Time Series Forecasting

Introduction to Simulation Using Risk Solver Platform

Queuing Theory

Decision Analysis

Project Management Online

Filters

A binding greater than or equal to ( $\ge$ ) constraint in a minimization problem means that

Identify the different sets of basic variables that might be used to obtain a solution to this problem. $\mathrm { MAX } : \quad \mathbf { 8 \mathbf { X } _ { 1 } } + 4 \mathbf { X } _ { \mathbf { 2 } }$ Subject to: 5+5\leq20 6+2\leq18 ,\geq0