Exam 4: Sensitivity Analysis and the Simplex Method
Exam 1: Introduction to Modeling and Decision Analysis52 Questions
Exam 2: Introduction to Optimization and Linear Programming62 Questions
Exam 3: Modeling and Solving Lp Problems in a Spreadsheet88 Questions
Exam 4: Sensitivity Analysis and the Simplex Method72 Questions
Exam 5: Network Modeling72 Questions
Exam 6: Integer Linear Programming72 Questions
Exam 7: Goal Programming and Multiple Objective Optimization59 Questions
Exam 8: Nonlinear Programming and Evolutionary Optimization68 Questions
Exam 9: Regression Analysis76 Questions
Exam 10: Discriminant Analysis57 Questions
Exam 11: Time Series Forecasting111 Questions
Exam 12: Introduction to Simulation Using Risk Solver Platform65 Questions
Exam 13: Queuing Theory79 Questions
Exam 14: Decision Analysis102 Questions
Exam 15: Project Management Online61 Questions
Select questions type
To convert=constraints into = constraints the Simplex method adds what type of variable to the constraint?
(Multiple Choice)
4.9/5  (40)
(40)
If the shadow price for a resource is 0 and 150 units of the resource are added what happens to the objective function value?
(Multiple Choice)
4.7/5  (34)
(34)
Exhibit 4.1
The following questions are based on the problem below and accompanying Risk Solver Platform (RSP) sensitivity report.
Carlton construction is supplying building materials for a new mall construction project in Kansas. Their contract calls for a total of 250,000 tons of material to be delivered over a three-week period. Carlton's supply depot has access to three modes of transportation: a trucking fleet, railway delivery, and air cargo transport. Their contract calls for 120,000 tons delivered by the end of week one, 80% of the total delivered by the end of week two, and the entire amount delivered by the end of week three. Contracts in place with the transportation companies call for at least 45% of the total delivered be delivered by trucking, at least 40% of the total delivered be delivered by railway, and up to 15% of the total delivered be delivered by air cargo. Unfortunately, competing demands limit the availability of each mode of transportation each of the three weeks to the following levels (all in thousands of tons):
Week Trucking Lanrits Railway Limits Air Carga Lavits 1 45 60 15 2 50 55 10 3 55 45 5 Costs (\ per 1000 tors) \ 200 \ 140 \ 400 The following is the LP model for this logistics problem.

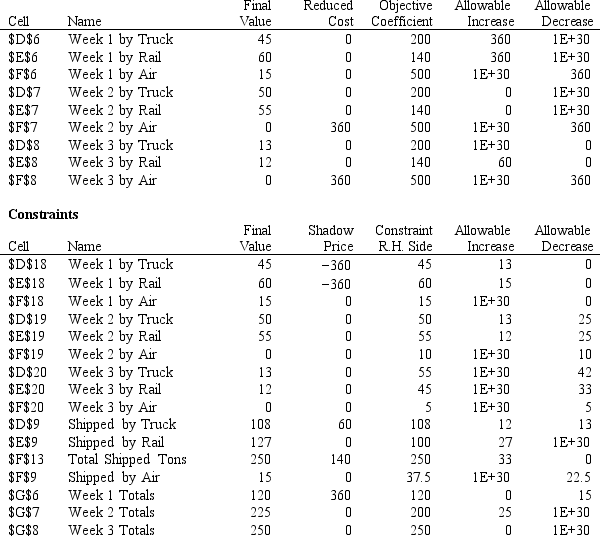 -Refer to Exhibit 4.1. Should the company negotiate for additional air delivery capacity?
-Refer to Exhibit 4.1. Should the company negotiate for additional air delivery capacity?
(Essay)
4.8/5  (42)
(42)
A variable with a final value equal to its simple lower or upper bound and a reduced cost of zero indicates that
(Multiple Choice)
4.7/5  (33)
(33)
Use slack variables to rewrite this problem so that all its constraints are equality constraints.
MIN:
Subject ta:
4+3\geq24 2+4\geq24 ,\geq0
(Essay)
4.9/5  (38)
(38)
Which of the constraints are binding at the optimal solution for the following problem and Risk Solver Platform (RSP) sensitivity output?
MAX : 7+4 Subject ta: 2+\leq10 +\leq10 2+5\leq40 \geq
Final Reduced Objective Allowable Allowable Cell Name Value Cost Coefficient Increase Decrease \ \ 4 Number to make: 1 6 0 7 1 3 \ \ 4 Number to make: 2 4 0 4 3 0.5
Final Shadow Constraint Allowable Allowable Cell Name Value Price R.H. Side Increase Decrease \ \ 8 Used 16 3 16 4 2.67 \ \ 9 Used 10 1 10 1 2 \ \ 10 Used 32 0 40 1E+30 8
(Essay)
4.8/5  (35)
(35)
A manager should consider how sensitive the model is to changes in all of the following except
(Multiple Choice)
4.7/5  (31)
(31)
The difference between the right-hand side (RHS) values of the constraints and the final (optimal) value assumed by the left-hand side (LHS) formula for each constraint is called the slack and is found in the .
(Multiple Choice)
4.8/5  (37)
(37)
A solution to the system of equations using a set of basic variables is called
(Multiple Choice)
4.8/5  (40)
(40)
Jones Furniture Company produces beds and desks for college students. The production process requires carpentry and varnishing. Each bed requires 6 hours of carpentry and 4 hour of varnishing. Each desk requires 4 hours of carpentry and 8 hours of varnishing. There are 36 hours of carpentry time and 40 hours of varnishing time available. Beds generate $30 of profit and desks generate $40 of profit. Demand for desks is limited so at most 8 will be produced.
How much can the price of Desks drop before it is no longer profitable to produce them? Base your response on the following Risk Solver Platform (RSP) sensitivity output.
Laet
= Number of Beds to produce = Number of Desks to produce The LP model for the problem is
Subject to: 6+4\leq36 (carpentry) 4+\leq40 (varnishing \leq demand for ,\geq0
Final Shadow Constraint Allowable Allowable Cell Name Value Price R.H. Side Increase Decrease \ \ 8 Carpentry Used 36 2.5 36 24 16 \ \ 9 Varnishing Used 40 3.75 40 26.67 16 \ \ 10 Desk demand Userl 3 0 8 1+30 5
(Short Answer)
4.7/5  (36)
(36)
Exhibit 4.1
The following questions are based on the problem below and accompanying Risk Solver Platform (RSP) sensitivity report.
Carlton construction is supplying building materials for a new mall construction project in Kansas. Their contract calls for a total of 250,000 tons of material to be delivered over a three-week period. Carlton's supply depot has access to three modes of transportation: a trucking fleet, railway delivery, and air cargo transport. Their contract calls for 120,000 tons delivered by the end of week one, 80% of the total delivered by the end of week two, and the entire amount delivered by the end of week three. Contracts in place with the transportation companies call for at least 45% of the total delivered be delivered by trucking, at least 40% of the total delivered be delivered by railway, and up to 15% of the total delivered be delivered by air cargo. Unfortunately, competing demands limit the availability of each mode of transportation each of the three weeks to the following levels (all in thousands of tons):
Week Trucking Lanrits Railway Limits Air Carga Lavits 1 45 60 15 2 50 55 10 3 55 45 5 Costs (\ per 1000 tors) \ 200 \ 140 \ 400 The following is the LP model for this logistics problem.

 -Refer to Exhibit 4.1. The Week 1 by Truck and Week 1 by Rail constraints each have a shadow price of -360. What do these values imply?
-Refer to Exhibit 4.1. The Week 1 by Truck and Week 1 by Rail constraints each have a shadow price of -360. What do these values imply?
(Essay)
4.9/5  (33)
(33)
A change in the right hand side of a binding constraint may change all of the following except
(Multiple Choice)
4.9/5  (37)
(37)
Risk Solver Platform (RSP) provides all of the following reports except
(Multiple Choice)
4.9/5  (27)
(27)
When performing sensitivity analysis, which of the following assumptions must apply?
(Multiple Choice)
4.9/5  (30)
(30)
What are the objective function coefficients for X1 and X2 based on the following Risk Solver Platform (RSP) sensitivity output?
Target Cell Name Value \ \ 5 Unit profit: OBJ. FN. VALUE 58
Adiustable Lower Target Upper Targel Cell Name Value Limit Result Limit Result \ B \ 4 Number to make: 1 6 0 16 6 58 \ C \ 4 Number to make 2 4 6 42 4 58
(Essay)
4.7/5  (31)
(31)
Showing 41 - 60 of 72
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)