Exam 11: Experimental Design and Analysis of Variance
Exam 1: An Introduction to Business Statistics63 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Methods100 Questions
Exam 3: Descriptive Statistics: Numerical Methods141 Questions
Exam 4: Probability127 Questions
Exam 5: Discrete Random Variables150 Questions
Exam 6: Continuous Random Variables145 Questions
Exam 7: Sampling and Sampling Distributions131 Questions
Exam 8: Confidence Intervals149 Questions
Exam 9: Hypothesis Testing150 Questions
Exam 10: Statistical Inferences Based on Two Samples139 Questions
Exam 11: Experimental Design and Analysis of Variance98 Questions
Exam 12: Chi-Square Tests112 Questions
Exam 13: Simple Linear Regression Analysis140 Questions
Exam 14: Multiple Regression and Model Building150 Questions
Exam 15: Process Improvement Using Control Charts117 Questions
Select questions type
Find a Tukey simultaneous 95 percent confidence interval for μ1 - μ2,where 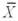 1 = 33.98,
1 = 33.98, 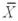 2 = 36.56,and MSE = 0.669.There were 15 observations total and 3 treatments.Assume that the number of observations in each treatment is equal.
2 = 36.56,and MSE = 0.669.There were 15 observations total and 3 treatments.Assume that the number of observations in each treatment is equal.
(Short Answer)
4.7/5  (36)
(36)
If the total sum of squares in a one-way analysis of variance is 25 and the treatment sum of squares is 17,then what is the error sum of squares?
(Short Answer)
4.9/5  (37)
(37)
The experimentwise α for the 95 percent individual confidence interval for μ1 - μ2 (treatment mean 1 - treatment mean 2)will always be smaller than the experimentwise α for a Tukey 95 percent simultaneous confidence interval for μ1 - μ2.
(True/False)
4.8/5  (34)
(34)
In a ___________________ experimental design,independent random samples of experimental units are assigned to the treatments.
(Multiple Choice)
4.8/5  (35)
(35)
In one-way ANOVA,the total sum of squares is equal to _______________________.
(Multiple Choice)
4.8/5  (39)
(39)
Consider the following calculations for a one-way analysis of variance from a completely randomized design with 20 total observations. 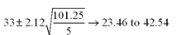 Compute a 95 percent confidence interval for the first treatment mean.
Compute a 95 percent confidence interval for the first treatment mean.
(Short Answer)
4.8/5  (37)
(37)
Consider the following partial analysis of variance table from a randomized block design with 10 blocks and 6 treatments. 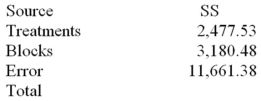 Test H0: there is no difference between blocks at α = .05.
Test H0: there is no difference between blocks at α = .05.
(Short Answer)
4.9/5  (35)
(35)
When we compute 100(1 - α)confidence intervals,the value of α is called the
(Multiple Choice)
4.9/5  (38)
(38)
In performing a one-way ANOVA,the _________ is the between-group variance.
(Multiple Choice)
4.8/5  (30)
(30)
A ___________ design is an experimental design that compares v treatments by using d blocks,where each block is used exactly once to measure the effect of each treatment.
(Multiple Choice)
4.8/5  (42)
(42)
Interaction exists between two factors if the relationship between the mean response and one factor depends on the other factor.
(True/False)
4.8/5  (31)
(31)
Consider the following partial analysis of variance table from a randomized block design with 10 blocks and 6 treatments. 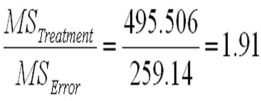 What is the block mean square?
What is the block mean square?
(Short Answer)
4.8/5  (37)
(37)
A one-way analysis of variance is a method that allows us to estimate and compare the effects of several treatments on a response variable.
(True/False)
4.8/5  (43)
(43)
The ___________________ units are the entities (objects,people,etc. )to which the treatments are assigned.
(Multiple Choice)
4.8/5  (32)
(32)
Find a Tukey simultaneous 95 percent confidence interval for μC - μB,where 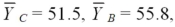 and MSE = 6.125.There were 4 treatments and 24 observations total,and the number of observations were equal in each group.
and MSE = 6.125.There were 4 treatments and 24 observations total,and the number of observations were equal in each group.
(Short Answer)
4.7/5  (38)
(38)
Consider the one-way ANOVA table. 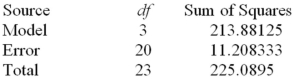 If there are an equal number of observations in each group,then each group (treatment level)consists of how many observations?
If there are an equal number of observations in each group,then each group (treatment level)consists of how many observations?
(Short Answer)
4.8/5  (39)
(39)
Consider the following partial analysis of variance table from a randomized block design with 10 blocks and 6 treatments. 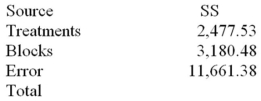 Test H0: there is no difference between treatment effects at α = .05.
Test H0: there is no difference between treatment effects at α = .05.
(Essay)
4.7/5  (30)
(30)
In randomized block ANOVA,the sum of squares for factor 1 equals:
(Multiple Choice)
4.8/5  (31)
(31)
Consider the one-way ANOVA table. 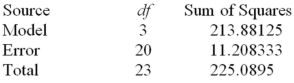 What is the treatment mean square?
What is the treatment mean square?
(Short Answer)
4.9/5  (35)
(35)
Consider the following partial analysis of variance table from a randomized block design with 6 blocks and 4 treatments. 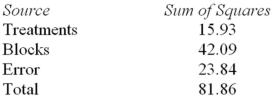 What is the block mean square?
What is the block mean square?
(Short Answer)
4.8/5  (28)
(28)
Showing 41 - 60 of 98
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)